复杂系统误差传递的主次作用分析与控制
2013-11-19唐冰松王增会
唐冰松, 王增会
(大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116024)
大量的工程实际应用表明,若某个物理量的观测结果存在误差,造成误差的原因极有可能是系统误差和随机误差共同作用的结果.为了最大程度上消除或减轻误差对观测结果的影响,需要研究系统误差和随机误差相互作用机制以及对最终观测结果的影响.著名学者费业泰[1]曾通过一些数学模型来解释系统误差和随机误差两者之间的关系,在动态测试与分析领域的误差估计建立了理论模型,但在实际的工程应用中并没有实质性的突破.国内外众多学者都对误差建立各种模型,但一直没有达成共识.文献[2]对复杂系统的分级误差模型的建立和传递函数的收敛性等问题进行了详细地阐述.文献[3]采用误差补偿热模态分析法对一个模具的模态进行分析.文献[4]对应变软化材料的数值稳定性进行分析,计算了数值模型的误差.文献[5]对低延性材料进行试验分析,得出应变误差与材料的几何参数有直接的关系,应力误差高度依赖于应力场.文献[6]对一个大坝水库模型在涨潮时的边界条件进行模拟,并研究了在涨潮时计算模型的误差问题.但这些模型对解释误差在传递过程中的发散和收敛效应以及当存在多个子系统时,哪个子系统对误差的传递占主导作用等问题都没有给出明确的解释和说明,而这些问题恰恰是解决误差的成分识别和控制等核心问题的关键所在.文中的主要目的是根据复杂系统随机误差和系统误差的相互关系和传递特征,建立一个以误差传递函数为基础的误差传递模型,并分析该复杂系统中各子系统的误差在观测目标误差中的主次作用,以系统论的角度旨在揭示影响观测目标误差的各种因素和形成机制.
1 系统误差和随机误差的合成
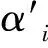
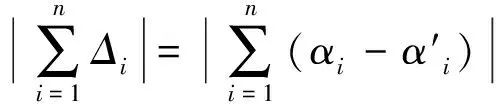
(1)
|∑Δi|经过多次测量后误差会出现逐渐递增或累计快慢呈周期性变化的情况.通过各种计算方法难以消除系统误差的存在,若要从根本上改进系统误差,必须从源头上查找造成系统误差的原因,进而改善观测结果.
随机误差(random error,RE)主要是由很多暂时未能掌握或不便掌握的微小因素引起的.通常情况下随机误差服从正态分布N(μ,σ2).

(2)
随机误差在实验测量的过程中不可避免,为了最大限度地降低对观测目标产生的影响,应尽量采用高效的处理手段消除随机误差对观测结果的影响.
若系统同时存在系统误差和随机误差,并且对该系统的测量值均有影响[7],则不仅需要同时考虑这两种误差,还需要分析两种误差的耦合效应对测量结果的影响.若指标i的系统误差标准差可以表示为αi,随机误差标准差可以表示为βi,则该指标总误差的标准差构成可表示为:
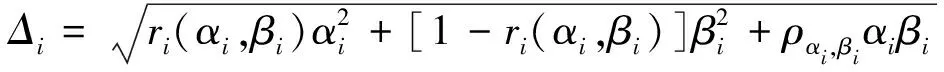
(3)
其中ri(αi,βi)是与αi,βi相关的权系数,ραi,βi为αi,βi的相关系数.
若ri(αi,βi)=1或ri(αi,βi)=0,则ραi,βi=0.Δi关于αi,βi的全微分可表示为:
2(1-ri)βi-ραi,βiαi]dβi
(4)
式(4)表明单个指标总的误差方差梯度不仅和SE,RE有关,和权系数ri也有关.
随着人们对系统误差的认识逐步深入,系统误差对总误差影响将逐渐减小.若αi=0,则Δi=βi,即仅留RE标准差项,Δi可以采用统计的方法分离,从而得到测试指标的真值.
2 系统误差与随机误差的分离与传递
为了能够清楚地叙述问题的本质,拟建立一个简单的数学模型来加以分析,如图1.
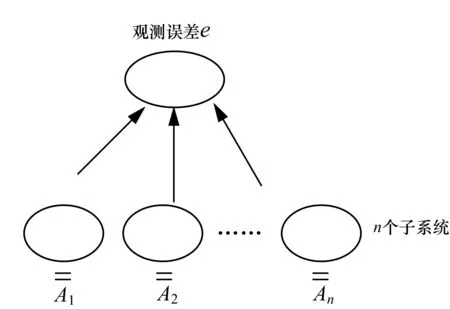
图1 观测误差与各子系统误差之间的传递关系Fig.1 Transferring relationship between target parameter and parameters in subsystems
设观测结果的误差由系统误差、随机误差以及两者的耦合项组成,表示为:
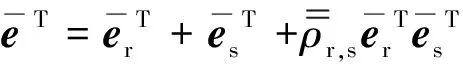
(5)
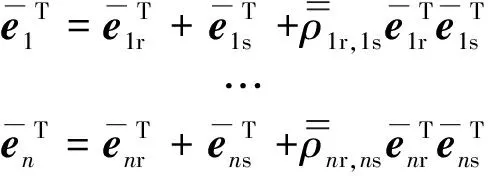
(6)
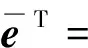
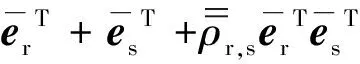
(7)
即:
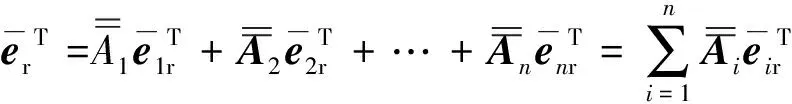
(8)

(9)
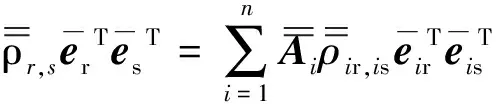
(10)
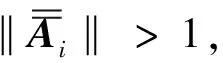
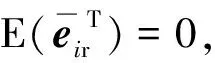
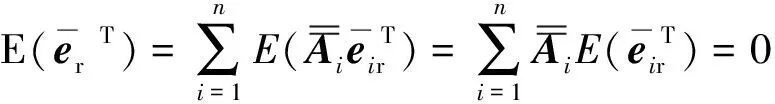
(11)
一般认为,式(10)在观测目标误差中所占的比重比较小,可以忽略不计,因此经过多次观测后,式(5)可以改写成
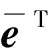
(12)
3 子系统误差传递主次作用的度量
1≤i≤n
(13)
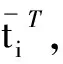
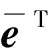
(14)
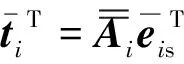
(15)
令

(16)
则
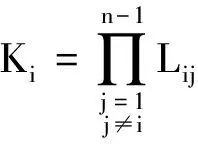
(17)
式(17)表明功能系数可以表示为所考察子系统与其它子系统传递函数范数之比的乘积,Lij>0.现对Ki与Lij进行讨论:
1) 若0 2) 若Lij>1,表明第i个子系统的传递作用大于第j个子系统的传递作用,前者相对于后者起到主导作用; 在实际研究中,如何确定传递函数的表达式一直以来为广大学者和工程师所关心,但能够给出传递函数解析解的却非常稀少,绝大部分传递函数无法给出解析解,只能得到数值解甚至无法用数学表达式进行表达.一些学者也采用各种方法研究如何能够得到传递函数的方法,如,文献[8]采用理论分析的方法给出了平壁导热传递函数的理论表达式;文献[9]采用数值的方法给出了脉冲锤击传递函数的数值方法;文献[10]采用“标定”的办法给出数字地震仪系统的传递函数.这些方法一般只针对特定的情况才能得到较好的结果,目前还缺乏能够解决这一问题的公认的理论和方法.若能得到各子系统的传递函数,则根据文中提出的子系统误差传递主次作用理论就能确定影响观测目标的“主要”与“次要”子系统,进而确定误差分析与控制主要的研究目标. 子系统1,2,3对总观测目标的误差贡献为: (18) (19) (20) 误差的分析与控制在工程实际应用中十分重要.文中从系统的角度研究了子系统误差在总误差中的传递机制及其互相作用,通过计算实例分析了误差传递过程中各子系统误差传递过程中的主次作用,为误差溯源、控制误差,提高观测目标的精确性指明了方向.在实际应用中,如何对一个复杂的系统进行划分,划分成互相独立的若干个子系统,进而确定各个子系统的目标参数,也是复杂系统误差分析中亟待解决的问题. [1] 费业泰. 精度理论若干问题研究进展与未来[J]. 中国机械工程, 2000,11(3):255-257. Fei Yetai. The development and tendency of some research problems on accuracy[J].ChinaMechanicalEngineering,2000,11(3):255-257.(in Chinese) [2] 唐冰松,韩晓林. 结构动力学有限元模型的参数识别误差溯源及正向传递[J].兰州理工大学学报, 2013,39(4):132-137. Tang Bingsong,Han Xiaolin.Error tracing and propagating positively of parameter identification based on dynamical finite element model of structure[J].JournalofLanzhouUniversityofScienceandTechnology,2013,39(4):132-137.(in Chinese) [3] Yang Jianguo,Yuan Jingxia, Li Jun. Thermal error analysis and robust modeling for error compensation on a CNC turning centre[J].InternationalJournalofMachineTools&Manufacture,1999,36:1367-1381. [4] Kulnarni M,Belytschco T,Bayliss A. Stability and error analysis for time integators applied to strain-softing material[J].ComputerMethodsinAppliedMechanicsandEngineering,1995,124:335-363. [5] Koubaa S,Othman R,Zouari B,et al. Finite-element analysis of errors on stress and strain measurements in dynamic tensile testing of low ductile materials[J].ComputersandStructure,2011,89:78-90. [6] Bouaanani N,Miquel B.A new formulation and error analysis for vibrating dam-reservoir system upstream transmitting boundary condition [J].JournalofSoundandVibration,2010,329:1924-1953. [7] 许桢英, 费业泰, 陈晓怀. 动态精度理论研究与发展[J]. 仪器仪表学报, 2001,22(4z): 70-74. Xu Zhenying, Fei Yetai, Chen Xiaohuai. The research and development of dynamical accuracy theory[J].ChineseJournalofScientificandInstrument(Additional),2001,22(4):70-74.(in Chinese) [8] 胡亚才, 姜周曙, 沈杏云,等.平壁导热传递函数研究[J]. 浙江大学学报, 1998,32(6):761-768. Hu Yacai,Jiang Zhoushu,Shen Xingyun,et al. The study of the transfer function of heat conduction in flat plane[J].JournalofZhejiangUniversity,1998,32(6):761-768.(in Chinese) [9] 王建文. 脉冲锤击的传递函数计算方法研究[J]. 应用声学, 2011,30(5):360-365. Wang Jianwen. A study on the transfer functionestimation algorithms of impulse hammer excitation[J].AppliedAcoustics,2011,30(5):360-365.(in Chinese) [10] 颜其中, 何家斌, 高杰. 数字地震仪系统传递函数的一种计算方法[J]. 地震学报, 2003,25(6):667-672. Yan Qizhong, He Jiabin, Gao jie. A method for calculating the transfer function of digital seismograph system[J].ActaSeimographSinica,2003,25(6):667-672.(in Chinese)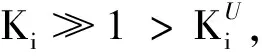
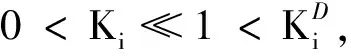
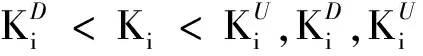
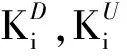
4 算例
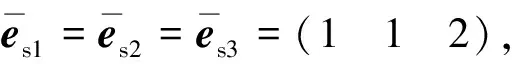

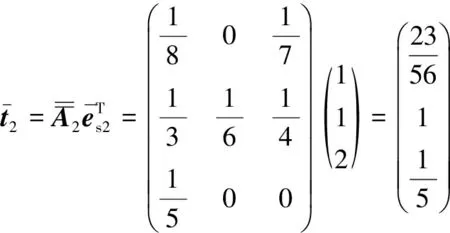
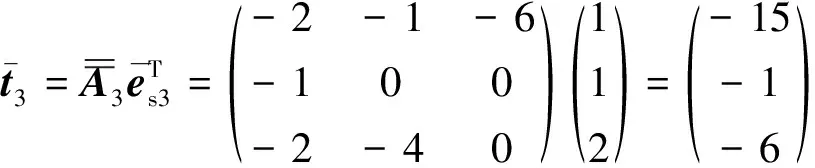
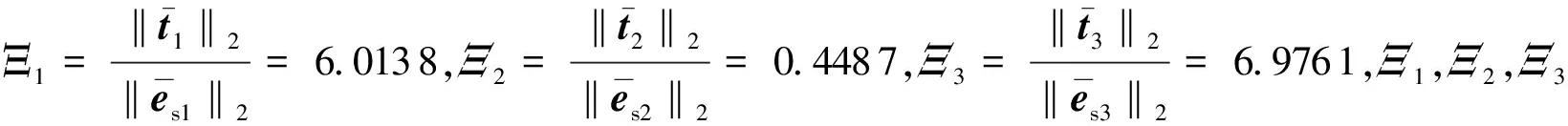
5 结论
