运动员空中翻腾和转体姿态控制过程中转动惯量的变化
2013-11-17郝卫亚王智艾康伟
郝卫亚 王智 艾康伟
国家体育总局体育科学研究所(北京100061)
在跳水、体操、蹦床、花样滑冰等技巧性运动项目中,旋转和美学是评分的主要因素。运动员空中旋转动作通常包括翻腾(somersault,绕重心横轴旋转)和转体(绕重心纵轴旋转,twist)两种基本运动形式。完美地完成空中翻腾和转体动作、完成更多的翻腾和/或转体的角度(或周数)是空中技术动作的关键,也是取得优异成绩的保证。另一方面,空中动作完成后,运动员要完成着落地、入水或落网动作。在这个阶段,运动员面临巨大的冲击负荷,运动损伤发生率也最高[1,2]。损伤常由于落地(水、网)时身体姿态不够理想造成[1,2]。因此,运动员需要在空中精确控制身体姿态,既最大限度地完成空中高难度动作,又要使身体在落地(水、网)时保持良好姿态。
影响运动员空中旋转动作的因素主要有三个方面:起跳或者离开器械时运动员初始姿态、运动速度、角速度等;空中肢体的动作控制;运动员自身的力学和生理机能特征[3]。这三个方面相互作用,形成十分复杂的交互关系[3]。在空中,运动员通过肢体动作,例如屈体、摆臂、团身等动作,改变身体的转动惯量,调节翻腾和转体的速度、角度,达到控制屈体运动姿态的目的[3,4]。转动惯量是物体的转动质量(angular mass),即物体对角加速度的惯量,正如质量是对线加速度的惯量。对在力学的任何质量系统,无论其如何运动,在三维空间的三个正交方向上都存在三个主转动惯量[5]。运动员在空中正是通过空中肢体动作调节三个主转动惯量来控制空中姿态[3,5]。但目前尚无关于运动员空中姿态控制中的转动惯量动态变化的研究。本实验针对不同类型的跳水空中技术动作,建立人体多刚体系统生物力学模型,利用多体系统质量几何计算方法研究人体空中翻腾和转体动作,分析对比不同动作中运动员转动惯量的变化特征。
1 方法
1.1 人体空中姿态与运动的确定
通常情况下,描述处于三维空间中刚体的位置和姿态,需要依靠三个空间位置量和三个方位角。与一般的刚体不同,人体是由多个环节组成的复杂形体,不能仅靠三个位置量和三个姿态角全面描述人体运动,需要提供多个关节的三维坐标数据。故描述人体运动远复杂于一般刚体,更具挑战性。
1.1.1 连体坐标系和参考坐标系
通常使用两个坐标系描述刚体在空间的运动。一个坐标系是固结于“绝对”空间或者邻接的其它刚体,称它为参考坐标系er;另一个坐标系与该刚体固接,称为连体坐标系(或者局部坐标系)eb[5]。刚体在参考坐标系中的姿态由连体坐标系eb关于er的方向余弦矩阵Trb完全确定。然而,刚体力学分析常引入一些被称为姿态坐标的变量来描述刚体的姿态[5]。在人体空中运动中,可以引入外方位角和内方位角描述人体在空中的姿态[6,7]。
1.1.2 外方位角和内方位角
在空中运动中,人体外方位角是固接于人体躯干的连体坐标系相对于地面的“绝对”参考坐标系之间的姿态角。连体坐标系ef固接于人体躯干,随着躯干旋转,它的三个坐标轴分别取人体的横轴、矢状轴和纵轴;参考坐标系ei固结于地面,并不旋转(图1)。

图1 人体空中运动的外方位角示意图
这时,人体的空中翻腾、倾斜和转体运动分别为绕上述三个坐标轴的运动。在如图1所示姿态角为φ、θ和ψ的旋转运动下,外方位角的方向余弦矩阵为:
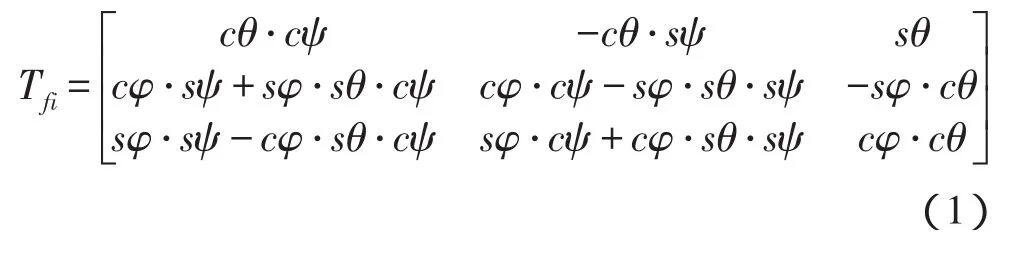
其中sφ=sinφ,cφ=cosφ。其它依此类推。通过上述矩阵可以将相对坐标系中的位置量xi转换为参考坐标系中的位置量xf。

其中xc为相对坐标系 f原点在参考坐标系的位置量。
在空中运动中,人体姿态构形由一系列的相邻两个环节之间相对角度确定,这些角度称为内方位角。例如,左上臂与躯干之间的相对位置关系需要由三个角度确定。在本研究中,采用卡尔丹角坐标(Cardan coordinate)确定左上臂与躯干之间的方位角,它的方向余弦矩阵为:

其中α、β和γ为卡尔丹角坐标。在卡尔丹角坐标下,环节的角速度为:

1.1.3 全局关节坐标
完成描述躯体在空间姿态的人体外方位角和内方位角的定义和计算后,我们将人体三维运动学分析获得的身体各关节三维坐标转换为外方位角和内方位角,以及全身重心的三维坐标。转换过程需要一系列坐标平移、旋转变换计算,也可以按照不同环节之间卡尔丹角的变化,通过差分方法计算环节角速度。
1.2 空中运动的力学与模型
1.2.1 空中运动的角动量守恒原理
在空中运动阶段,空气阻力可以忽略,全身重心轨迹为抛物线,抛物线轨迹取决于质心的初始位置和速度。运动员起跳或者离开器械后,重心质心的轨迹就确定了,运动员在空中完成的任何动作都改变不了质心运动轨迹。另一方面,无论何种空中运动形式,运动员在空中的运动中都遵循角动量守恒原理。运动员在空中只受通过重心的自身重力作用,所以运动员在起跳后相对于质心的角动量保持不变:

其中H0为起跳初始的角动量矢量,I为全身总转动惯量张量,ω为角速度矢量。从式(5)可看出,空中运动过程中,转动惯量与角速度成反比。事实上,运动员腾空后,在内力作用下,可以通过改变身体的转动惯量(即改变身体姿势加大或减小转动半径)调节旋转速度,但总动量矩保持不变。运动员可以采用屈体或团身等动作加快转动角速度,也可以通过张开身体降低转动角速度。
1.2.2 空中运动生物力学模型
根据跳水、体操等运动项目空中翻腾和转体技术动作的运动特征,本文建立了11环节的人体模型。模型包括头、上躯干、下躯干、骨盆、左右上臂、左右前臂和手、左右大腿、左右小腿和足11个环节。环节之间由通过不同自由度的铰链连接。模型共有21个自由度,其中左右肩关节、左右髋关节由3个自由度的球铰链连接;左右肘关节、左右膝关节、颈关节则由1个自由度的柱铰链连接;上-下躯干之间、下躯干-骨盆之间由2个自由度(可以绕垂直轴和冠状轴旋转)的铰链连接。
1.2.3 计算转动动量
上述人体模型可以抽象成这样一个多刚体系统[8]:系统由11个环节Sk(k=1,...,11)构成,他们由10个连接点Ok(k=2,…,11)连接,连接系统从S1开始发源。刚体系统相对于其质心的角动量可以由一系列函数项的和表示,每项是一个相对角速度的函数。如果设U为铰Ok的所有后继的刚体组合体,而L为包括B1在内的所有剩余的刚体组合体(图2),则h就是刚体系统的总角动量。

上式表明,多刚体系统在铰Ok发生转动时产生的转动动量仅与铰Ok处的角速度ωul有关,与其他角速度无关。

图2 关节Ok相关的位移与角速度矢量关系图
1.3 空中运动计算机仿真系统
人体空中运动计算机仿真系统是对跳水、体操等运动项目空中技术动作进行计算机仿真的数值计算及数据管理系统。仿真系统软件运行的操作系统为Windows XP,使用 Microsoft公司的 Visual C++6.0作为用户界面模块及数据管理模块部分的开发平台,采用MathWork公司的MATLAB 6.5作为数值计算模块部分的开发平台,之后利用MATLAB提供的引擎与Visual C++6.0编写的程序结合,完成整个系统的开发。整个人体空中运动模拟计算系统划分为三个功能模块:界面管理模块、数据管理模块和数值计算模块。
图3是人体空中技术动作模拟软件的一个操作模块的界面。模拟软件的四个操作模块可以以卡片方式切换,它们分别为空中运动计算、人体模型计算、人体参数输入和人体参数管理模块。空中运动计算模块是用来将人体模型计算的惯性参量和人体运动结合起来进行计算,而其他三个模块分别用来计算人体惯性参量、输入和管理人体形态学参数。

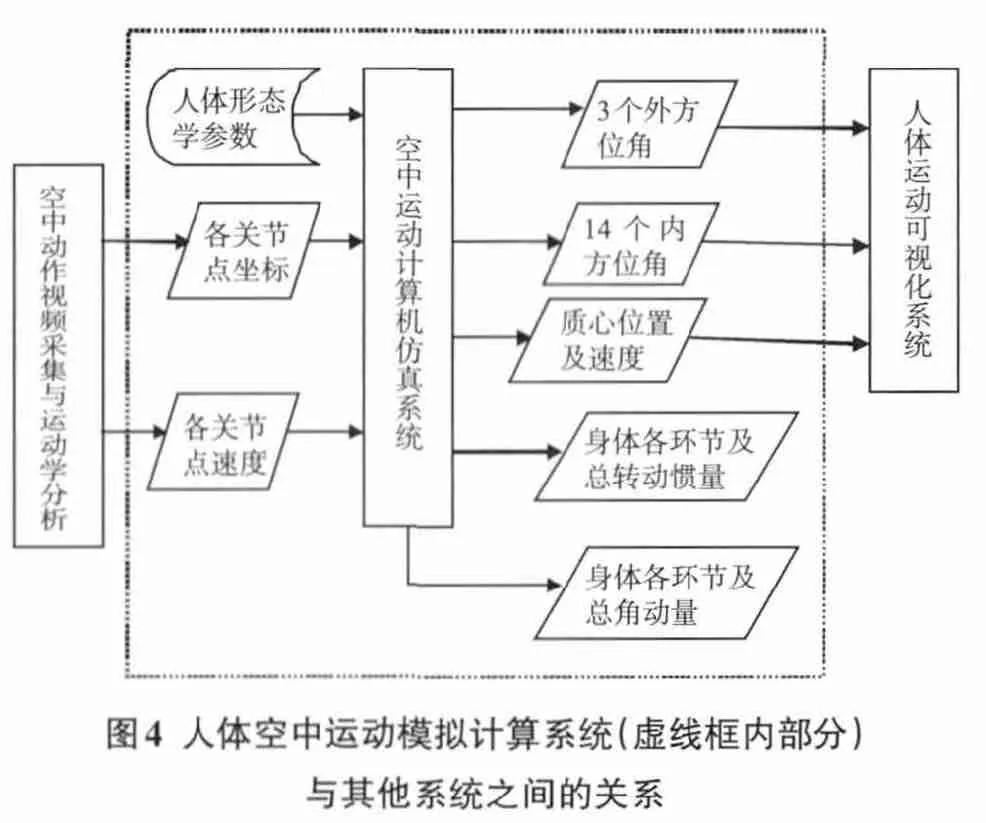
人体空中运动计算机仿真系统与其他系统之间关系如图4所示。空中运动计算机仿真系统的前端系统为运动项目的空中动作视频采集及三维运动学分析部分,提取人体空中运动过程中随时间变化的关节位移和速度的系统。这些随时间变化的各关节点的三维坐标和各关节点速度参数序列作为人体空中运动计算机仿真系统输入的一部分。同时输入人体模型所需要的95个人体测量参数[7]。通过该系统计算获得人体躯干空中姿态的3个方位角。这三个方位角结合14个内方位角输入人体运动可视化系统就可形成人体模型的可视化运动,以便观察分析动作[9]。
1.4 计算空中翻腾和转体姿态控制过程中的转动惯量
任何多体系统的转动惯量都是与质量分布有关的一个张量。人体系统在空中运动过程中,由于角动量恒定,主转动惯量影响人体系统围绕三个轴向运动的角速度和位移。在跳水、体操和蹦床等运动项目中,运动员通过屈体、手臂运动调整空中运动角速度,达到完成技术动作。
在公式(5)中以质心为基点的全身总转动惯量张量I的矩阵形式为:

式中 Ixx,Iyy,Izz称为环节刚体相对x,y,z各轴的转动惯量,也称惯量矩,Ixy,Ixz,Ixz称为环节刚体的惯量积。例如,Ixx和Ixy分别定义为

其他几个惯量矩和惯量积依此类推。根据力学原理和高等代数中证明,矩阵I为实对称矩阵,必可由相似正交变换转化为对角阵,使变换后的所有非对角线元素均为零。这时惯量矩阵有以下简单形式

对角线上元素I1,I2和I3称为刚体系统的中心主惯量矩。本文基于MATLAB 6.5语言开发了计算软件,将空中运动计算机仿真系统输出的运动员完成身体总转动惯量张量转化为主惯量矩。
1.5 空中技术动作的三维运动学分析
采用三米跳板跳水三维运动学分析的方法[10],对我国1名著名跳水运动员完成的四个不同类型的高难度跳水空中动作进行视频采集,之后采用Simi Motion运动分析软件解析动作,分别获得四个空中动作的各关节点坐标和速度数据[10]。四个动作是:A:向前翻腾三周半(107B),B:向内翻腾三周半抱膝(407C),C:向后翻腾一周半转体两周(5136B),D:向后翻腾一周半转体两周半(5235B)。之后,将所获得各关节点坐标和速度数据,以及运动员的人体形态学参数输入空中运动计算机仿真系统进行仿真计算。分析运动员在完成空中技术动作过程中的重心位移,反映身体姿态的内方位角(卡尔丹角),身体躯体相对地面运动的外方位角,以及运动员身体的主转动惯量等主要生物力学指标的变化过程。
2 结果
2.1 总质心位置随时间的变化
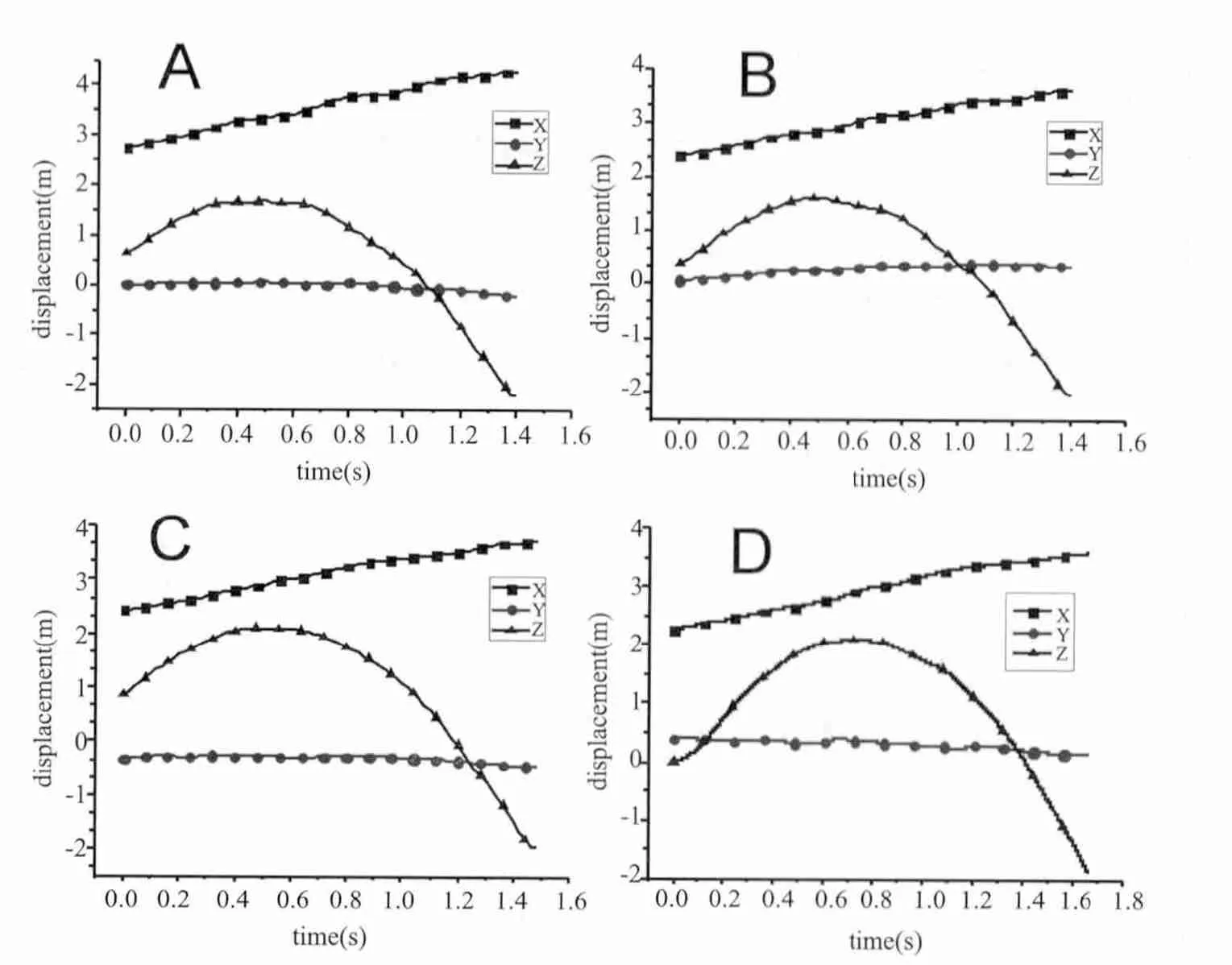
图5 空中动作的总质心位置随时间的变化曲线
图5为四个动作的总质心位置随时间的变化曲线。可以看出,运动员在空中运动中,重心垂直高度(Z方向)变化呈抛物线变化,基本无左右方向的侧向运动(Y方向),向前方向(X方向)呈匀速运动。这个结果符合生物力学的基本规律。
2.2 外方位角随时间的变化
外方位角变化反映运动员完成动作过程中,躯干部分翻腾、转体和躯干倾斜(tilt)的变化。由图6可看出,四个动作的所有翻腾和转体与实际完成技术动作基本相同。但也存在一些技术动作完成不完整的情况。如在动作A中,起跳时就有约0.2周的翻腾,而结束时有0.1周翻腾未完成。再如动作C是一个高难度动作,起跳时就有约0.5周的转体。动作C和D都是有转体的动作,运动员转体时身体需要作不对称肢体运动,躯干有一定的倾斜运动,完成后躯体倾斜应当随之消失。由图6C、D可以看出,动作C和D均有幅度约30~45°的周期性倾斜运动。动作A和B是两个无转体动作,因此倾斜运动幅度较小,呈现无规律的倾斜运动。

图6 空中动作的外方位角随时间的变化曲线
2.3 主转动惯量随时间的变化
图7为四个空中动作的主转动惯量随时间变化曲线。图中I1是与人体转体有关的主转动惯量,I2和I3是与翻腾和倾斜相关的两个主转动惯量。从4个动作的三个主转动惯量的变化曲线看,I2和I3比较接近,平均值约为I1的5倍。
动作A和B均是无转体动作。运动员起跳后,主要通过屈体或抱膝减少绕冠状轴的主转动惯量,完成翻腾。运动员完成动作A起跳时,身体未完全伸展,因此主转动惯量I2和I3均未达到最大,而在翻腾结束时达到最大值,I2在翻腾阶段平均为3.46 kg·m2,最大达到12.48 kg·m2,约为屈体条件下最小值的4.6倍,而I3最大值约为最小值的3.6倍;在翻腾过程中I1变化较小,平均为2.12 kg·m2。运动员在完成动作B起跳时身体完全伸展,I2和I3均达到最大值,I2约为13.62 kg·m2;随后迅速抱膝,降低I2以增加翻腾角速度;翻腾阶段I2平均为3.30 kg·m2;完成翻腾后又迅速伸展,增加I2以降低翻腾速度,为入水准备;I2最大值是屈体条件下最小值的4.8倍,I3最大值约为最小值的4.1倍。从时间看,动作A和动作B屈体或团身的动作阶段约0.2 s,保持屈体或者团身姿态下的翻腾动作约1s,为准备入水而展开身体的动作阶段约0.1s。
动作C和D均为转体动作,主转动惯量变化相似。开始阶段,I1相对较小,I2和I3则保持较大水平,且存在一定波动。这种波动是转体中的上臂摆动引起的。完成转体后,上臂打开,停止转体同时开始屈曲髋关节,使I2和I3迅速降低,加快翻腾动作。动作C转体阶段I1较小,平均为1.15 kg·m2,转体结束时可达到4.32 kg·m2;翻腾阶段I2最小,平均为3.65 kg·m2,结束时为12.95 kg·m2。动作C和动作D的转体阶段约1 s,翻腾阶段约0.6 s;动作C翻腾阶段比动作D稍长。
3 讨论
人体转动惯量对基本运动的影响,历来受到运动生物力学和运动医学界重视。Lee等[11]通过人体实验研究了转动惯量增加对转向跳跃(jump turn)运动的影响,结果发现,通过使用配重增加垂直轴转动惯量9倍后,转向角度增加44.7%,但地面反作用力的最大和平均力矩分别增加42%和90%;角动量则增加152%,跳跃时间增加30%。Pontzer等[12]研究了上臂摆动在行走和跑步中的作用,发现在无上臂重量条件下,上部身体转动惯量变化对头的垂直轴转动(yaw)和肩部相对于骨盆转动的相位有影响。Usherwood等[13]通过建立数学模型,分析了双足动物跑步时动能变化,认为增加身体俯仰轴(pitch,相当于人类的冠状轴)的转动惯量是一种有效的节能手段。Royer等[14]研究发现,改变下肢质量和转动惯量对受试者行走的能量消耗的影响相同。Browning等[15]则报道了增加下肢负重和转动惯量都导致行走时的能耗率增加。

图7 空中动作的主转动惯量随时间的变化曲线
人体转动惯量在很多体育动作中起着至关重要的作用。Ackland等[16]研究表明,女子体操运动员因发育生长,身体转动惯量增加,制约了运动员完成翻腾动作。花样滑冰项目中,三周和四周转体跳都是运动员追求的最高难度动作;在空中阶段,运动员转体速度主要依靠调节身体转动惯量控制;运动员起跳后要迅速有力地收缩上肢和下肢,在空中将上、下肢保持在人体垂直轴附近[17]。Bardy等[18]发现,在完成站立向后翻腾(backward standing somersaults)动作过程中,高水平受试者能够利用视觉调节控制身体的转动惯量,而新手受试者则无此能力。
人体操纵物体的转动惯量对人体运动行为的影响,也是人们关注的重要问题。Slota等[19]实验研究了人抓持不同重心位置和不同转动惯量物体时的策略,发现人主要通过两种机制调节抓持任务:改变抓力和重新分配正向和切向力矩。Langelier等[20]报道,在为温哥华冬奥会的加拿大运动员设计坐式滑雪器时,通过脚踏的倾斜度调整运动员和滑雪器的转动惯量,从而增加稳定性并提高运动表现。Liu等[21]采用一种动态转动惯量球拍训练运动员,发现8周训练后运动员的运动技术明显提高。
尽管转动惯量的作用在体育运动中受到的广泛关注,但目前尚无对运动(特别是空中运动)中人体系统的主转动惯量进行的系统研究。本文首先针对跳水空中技术动作的特点,建立了模拟空中技术动作的三维多体系统生物力学模型,提出有关空中动作过程中姿态与运动的数学模型。其次,根据空中运动过程中角动量守恒的原理,建立了运动专项空中技术动作生物力学模型的动力学方程。再次,本文基于VisualC++6.0和MATLAB 6.5,开发了包括用户界面模块、数据管理模块和数值计算模块的空中运动仿真软件。之后,应用多体系统质量几何计算方法,建立了空中运动过程中多体系统主惯量矩的计算方法,将空中运动计算机仿真系统输出的运动员完成身体总质心转动惯量张量转化为中心主惯量矩。最后,本文利用所开发的软件,对我国一名著名跳水运动员完成的4个跳水空中技术动作进行了个性化的(subject-specific)计算机仿真研究,并分析了运动员完成空中动作过程中主惯量矩的变化特征。
研究表明,本文建立的空中技术动作仿真方法是可行和有效的,建立的计算机方法可用来分析空中翻腾和转体姿态控制过程中转动惯量变化特征,为提高跳水、体操等运动项目运动技术训练水平,防止运动损伤发生提供新的科技手段。
[1]曲绵域,于长隆.实用运动医学.北京:北京大学医学出版社,2003:527-564
[2]任玉衡,田得祥.中国优秀运动员运动创伤流行病学研究.国家体育总局科技司,1999.
[3]Yeadon MR.The biomechanics of the human in flight.Am J Sports Med,1997,25(4):575-580.
[4]Hiley MJ,Yeadon MR.Optimisation of high bar circling technique for consistent performance of a triple piked somersault dismount.J Biomech,2008,41(8):1730-1735.
[5]洪嘉振.计算多体系统动力学.北京:高等教育出版社,1999,37-62.
[6]Yeadon MR.The simulation of aerial movement--I.The determination of orientation angles from film data.J Biomech,1990,23(1):59-66.
[7]Yeadon MR.The simulation of aerial movement--II.A mathematical inertia model of the human body.J Biomech,1990,23(1):67-74.
[8]Yeadon MR.The simulation of aerial movement--III.The determination of the angular momentum of the human body.J Biomech,1990,23(1):75-83.
[9]郝卫亚.人体运动的生物力学建模与计算机仿真进展.医用生物力学,2011,26(2):97-104.
[10]郝卫亚,艾康伟,王智,等.三米跳板跳水空中技术动作的三维运动学分析方法.首都体育学院学报,2005,17(3):63-65.
[11]Lee DV,Walter RM,Deban SM,et al.Influence of increased rotational inertia on the turning performance of humans.The Journal of Experimental Biology,2001,204:3927-3934.
[12]Pontzer H,Holloway JH 4th,Raichlen DA,et al.Control and function of arm swing in human walking and running.J Exp Biol,2009,212:523-534.
[13]Usherwood JR,Hubel TY.Energetically optimal running requires torques about the centre of mass.J R Soc Interface,2012,9:2011-2015.
[14]Royer TD,Martin PE.Manipulations of leg mass and moment of inertia:effects on energy cost of walking.Med Sci Sports Exerc,2005,37(4):649-656.
[15]Browning RC,Modica JR,Kram R,et al.The effects of adding mass to the legs on the energetics and biomechanics of walking.Med Sci Sports Exerc,2007,39(3):515-525.
[16]Ackland T,Elliott B,Richards J.Growth in body size affects rotational performance in women's gymnastics.Sports Biomech,2003,2(2):163-176.
[17]King DL.Performing triple and quadruple figure skating jumps:Implications for training.Can J Appl Physiol,2005,30(6):743-753.
[18]Bardy BG,Laurent M.How is body orientation controlled during somersaulting?J Exp Psychol:Human Perception and Performance,1998,24(3):963-977.
[19]Slota GP,Suh MS,Latash ML,et al.Stability Control of Grasping Objects with Different Locations of Center of Mass and Rotational Inertia.J Mot Behav,2012,44(3):169-178.
[20]Langelier E,Martel S,Millot A,et al.A sit-ski design aimed at controlling centre of mass and inertia.J Sports Sci,2013,31(10):1064-1073.
[21]Liu C,Liu YC,Kao YC,et al.Effects of training with a dynamic moment of inertia bat on swing performance.J Strength Cond Res,2011,25(11):2999-3005.
