通泰桥沥青路面车辙探讨

2013-11-16张淑菡陈艳金赵洁冰

交通运输研究 2013年2期

程鹏，张淑菡，陈艳金，赵洁冰

（张家口翰得交通公路勘察设计有限责任公司，河北张家口 075000）

0 引言

目前，国内桥面铺装设计寿命一般为15～20年，但在服务期限内都会或多或少地出现裂缝、波浪推移、局部拥包（沥青包、高温气包）及车辙等一种或多种破坏现象。其中车辙破坏最为常见，同时是使道路工作者担心的路面病害之一。这是由于车辙严重降低了路面的行车安全性，从而影响了高等级道路的投资效益。对车辙的控制和防治是目前迫切需要解决的问题，其中容许车辙深度是最为关键的指标之一。

本文采用理论分析与试验研究相结合的方法，利用ANSYS有限元软件对通泰大桥车辙进行分析和计算。

1 通泰大桥沥青路面车辙计算参数

1.1 材料粘弹性参数的确定

1.1.1 静态蠕变试验

为了预估沥青混凝土路面的车辙，需采用恰当的实验方法来确定本构方程中的材料参数，才能较为准确地模拟实际沥青混凝土路面的应力和变形状态。因此需要通过有效的实验手段来对建立的本构关系相对应的材料参数进行确定。通过长期分析发现，蠕变试验能够较好的模拟沥青混合料的粘弹性应变—时间关系，也能很好的对Burgers模型的材料参数进行求解。

采用澳大利亚UTM-100动态伺服液压沥青混合料试验系统进行试验，试验中电脑自动采集数据，将蠕变试验结果绘于以应变为纵轴，时间为横轴的坐标系内，通过蠕变曲线能很直观地了解沥青混合料的粘弹性变形特性，分析沥青混合料的变形随时间的变化关系。蠕变试验曲线如图1所示。

图1 SMA13的蠕变曲线

1.1.2 基于粒子群算法的Burgers模型参数拟合

图2 粒子群算法计算流程

粒子群算法的基本思想是用于优化问题的每一个解称为一个粒子，定义一个符合度函数来衡量每个粒子解的优越程度。每个粒子根据自己和其他粒子的“飞行经验”游动，从而达到从全空间搜索最优解的目的。参数拟合流程如图2所示。由静态蠕变试验所得到蠕变曲线关系图以及大量数据，根据Burgers模型加载、卸载过程中的蠕变关系方程，利用粒子群算法原理进行编程分析计算，输入蠕变实验数据（应变ε及时间t）并根据已有文献参考初值即可得到材料的Burgers的模型参数（E1、η1、E2、η2）。参数拟合结果如表1所示。

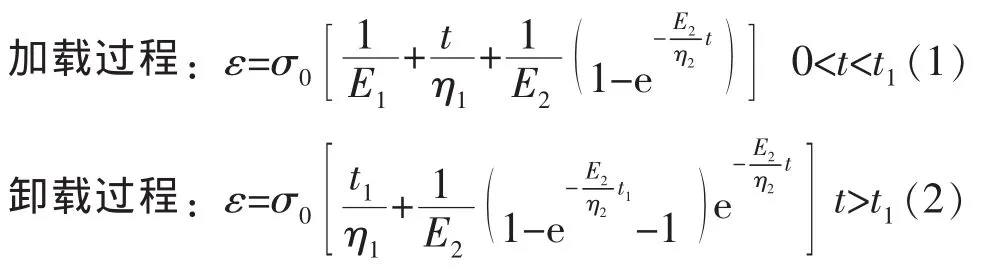
表1 材料的Burgers模型参数

1.2 道路交通条件

通泰大桥设计行车速度为60km/h，根据徐世法等人对轮载作用沥青路面上的“代表时间”的研究[1]，对该行驶速度范围内的车辆，统一将车辆作用时间简化定为0.015s以方便计算。确定后，每一点的累计加载时间就决定于车道轮载的横向分布系数。车道内的横向分布系数参考文献[2]，对于双向六车道道路的主车道，车道内轮迹的横向分布系数为0.33～0.36，本文按最严重的情况取推荐范围上限0.36。由此便可以得到轮载对路面的累加作用时间为：

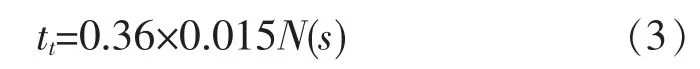
式中：N——累计当量轴次。

因此可计算出不同累计当量轴次下轮载对路面的累加作用时间（如表2所示）。

1.3 汽车荷载模型

将由路面不平整度产生的附加动荷载进行简化，使其形式更加简单以便于进行沥青路面车辙的计算。

现行路面设计方法采用竖向静载作用下弹性多层体系的理论模型。对于实际道路上行驶的车辆，由于路面不平整而产生振动，路面受到的车辆荷载随时间和路表特性改变而变化，是一个典型的动力荷载。根据汽车动力学的研究成果，汽车振动荷载的幅值一般为静载的0.05～0.6倍，这主要与车辆悬架特性、车速和路面不平整度等有关。为了使计算简便并使其结果具有代表性，也通过上述计算分析验证，取汽车振动荷载幅值为静载的0.3倍，并根据上述附加动荷载的建立得出了如下汽车动载模型方程：

式中：F(t)——汽车荷载；

P0——车轮静载；

ω——振动频率；

Pf′(t)——汽车振动荷载幅值，且

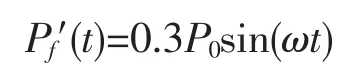
具体取值为：根据BZZ－100的标准，取单边单轴静载轮重，当车速为80km/h时，轮载作用时间取0.015s，由此可算ω=，T=0.015s。

以上取值经计算可得：

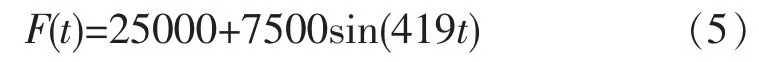
由于当量圆半径δ=0.1065m，式（5）所得汽车荷载换算为接地压强可得：

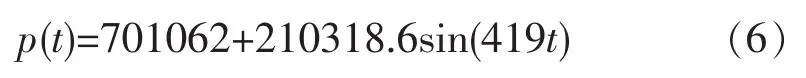
尽管该汽车动载模型形式简单，但对汽车特性、几何线形、路况及车速等多方面因素进行了综合考虑，计算简便，可以用来模拟汽车荷载。汽车荷载与时间的关系如图3所示。

图3 汽车荷载与时间的关系

通过ANSYS有限元分析软件中APDL（ANSYS Parametric Design Language参数化设计语言[3]）对汽车动载模型函数进行输入即可得到与图3汽车荷载与时间关系图一致的荷载典线。该车辆荷载模型与已有的模型相比，具有形式简单、便于计算的优点，且与几何曲线、路况及车速关系密切，可以用来模拟汽车荷载。对沥青路面进行加载，以便于进行车辙的分析。

1.4 代表温度

车辙是沥青路面高温季节的产物，它对温度有极高的敏感性，经研究表明，在温度低于20℃时，沥青混合料产生的永久变形可以忽略，所以不会产生车辙，因此，在车辙计算中可以只考虑路面温度高于20℃的月份。

虽然路面内温度场的一维热传导方程可以应用在不同边界条件和方法来求解该偏微分方程，得到温度场的解析式或直接算得不同时刻在不同深度处的温度值。但在实际的应用过程中，并不需要确切知道路面内任意处的温度。因此AI提出了确定路面代表温度的经验式，根据得出的温度值，来选择沥青以及其他材料。

AI认为沥青层的典型温度由下式决定：

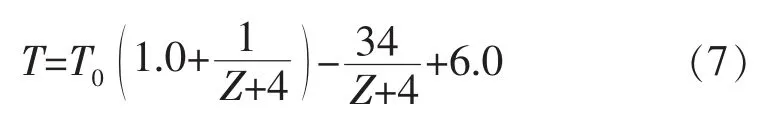
式中：T——路面月平均代表温度，℉；

T0——大气月平均温度，℉；

Z——沥青面层厚度的1/3厚度，英寸。

为了计算通泰大桥沥青路面的代表温度，统计了张家口地区1971～2000年的平均气温情况（如表3所示），并用AI方法计算了张家口地区不同月份沥青路面的代表温度。

表3 张家口平均气温统计（1971～2000年）

从表3可知，张家口地区4～9月路面代表温度高于20℃，代表温度区间23.3～31.9℃，取其平均温度作本文计算时的代表温度为27.9℃。

有了代表温度便可以通过插值得到在该代表温度下的前面通过蠕变试验得到的沥青混合料Burgers模型的参数，由此将温度问题转换为模型参数中在代表温度下的模量及Burgers模型参数来进行计算。

2 有限元模型计算方案

利用ANSYS有限元计算程序，建立桥面二维计算模型。考虑到结构及荷载作用的整体性，可建立沥青路面如结构B的实体模型进行分析。

模型建立后，计算单元沥青层采用PLANE182，聚丙烯纤维混凝土及正交异性钢桥面板则采用PLANE42。沥青面层为粘弹性材料，材料的本构模型采用Burgers模型在ANSYS内使用其的Prony级数形式，因此要进行输入必须对其进行相应的转换。聚丙烯纤维混凝土及正交异性钢桥面板则认为是完全弹性体系，材料本构模型采用广义虎克定律。选用路面结构的各层材料参数如表4所示，路面有限元模型如图4所示。

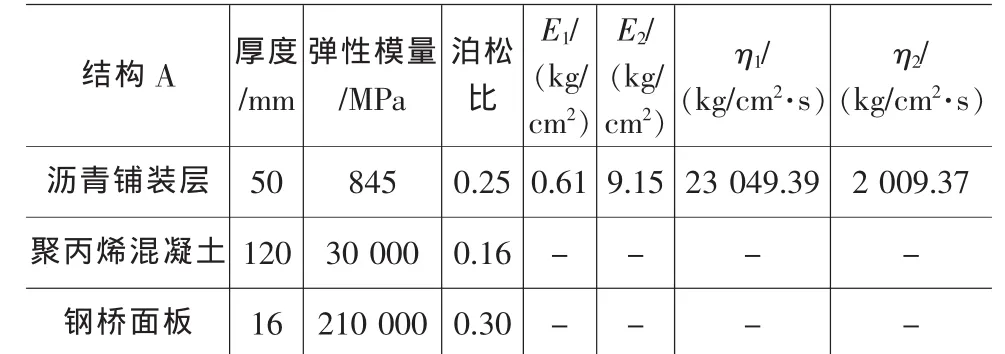
表4 通泰大桥计算模型材料参数

图4 ANSYS中桥面模型

3 有限元计算结果分析

3.1 不同加载次数的计算结果

采用加载次数10万次～2000万次对通泰大桥车辙深度即永久变形进行了计算，计算结果如图5所示。

图5 不同加载次数时的车辙

图5所示的是轴载作用次数与路面车辙之间的关系。随着轴载作用次数的增加沥青路面的车辙深度逐渐增大。在轴载作用次数的前期（＜100万次），路面车辙深度增长相对缓慢，当轴载作用次数达到100万次以后车辙增加速度有所增加。总体而言，此沥青桥面铺装抗车辙性能较好，当轴载次数达到2000万时，其车辙深度仅为3.978mm。

3.2 不同钢桥面板厚度的计算结果

为比较不同钢桥面板厚度对沥青铺装车辙的影响，计算了12mm、16mm、20mm三种钢板厚度情况下的沥青铺装车辙。计算结果如图6所示。

图6 不同钢桥面板厚度时的车辙

从以上图表看出，桥面沥青铺装车辙深度随着钢桥面板厚度增加表现出先增大后略有减小的趋势。但是，从增长的幅度来看，当钢桥面板厚度达到16mm，车辙深度最大为3.978mm，当钢桥面厚度为12mm时，车辙最大深度为3.727mm，前者相对于后者仅增加了6.7%。同时，3.978mm的车辙深度仍然处于很低的水平，远小于文献[4]中车辙的养护标准规定的15mm车辙深度。这表明，总体而言通泰大桥沥青铺装抗车辙能力强，而钢桥面板厚度对车辙深度的影响较小。

3.3 不同沥青铺装厚度的计算结果

为比较不同沥青铺装厚度对沥青铺装车辙的影响，计算了50mm、70mm、90mm三种沥青铺装厚度情况下的车辙。计算结果如图7所示。

图7 不同沥青铺装厚度时的车辙

从以上图表看出，当沥青铺装厚度为70mm时，车辙深度达到5.580mm，相对于50mm沥青铺装结构增加了1.602mm，增加幅度达到40.3%。当沥青铺装厚度为90mm时，车辙深度达到6.992mm，相对于70mm沥青铺装结构增加了1.412mm，增加幅度为25.3%。这表明通泰大桥沥青铺装车辙深度随着沥青铺装厚度增加而快速增加，但增加的趋势逐步放缓。从减小车辙的方面考虑，通泰大桥采用50mm单层铺装，其抗车辙效果好于采用双层沥青铺装的更厚的沥青铺装结构。