浅谈力矩分配法在计算有线位移刚架中的创新应用
2013-11-15周立军张国修
◆周立军 张国修
(日照职业技术学院建筑工程学院;山东省莒县第四高级中学)
力矩分配法只适用于无结点线位移的结构,对于有结点线位移的结构,除某些特殊结构可直接用力矩分配法计算(即用“无剪力分配法”)外,一般是联合应用力矩分配法与位移法进行计算,有些《结构力学》教材也介绍这种方法(即“传统法”)。本文将要介绍的方法,虽然其总的思路与“传统法”的思路基本相同,但其具体步骤却有区别,而且要比“传统法”更简单(即“简便法”)。
一、具体实例
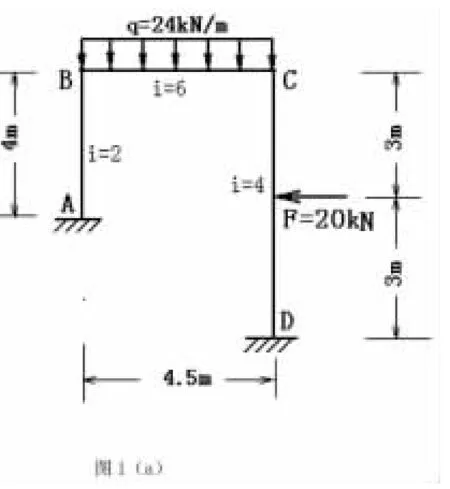
如图1(a)所示的刚架,画出在图示荷载F、q作用下的弯矩图。
该刚架在荷载F、q作用下不仅产生角位移,同时也产生侧向线位
移。针对该类题目我将采用传统做法和力矩分配法分别计算。
二、“传统法”计算
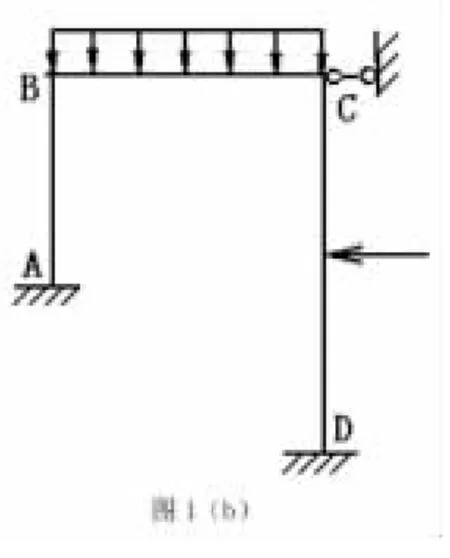
1.取基本体系如图1(b),即在其中结点c设置一
附加链杆,这样原结构便不会产生线位移,那么可应用力矩
分配法计算基本体系的各杆端弯矩(设用MF表示);
2.由计算得的杆端弯矩,通过平衡条件确定
某些杆的杆端剪力(设以 表示),
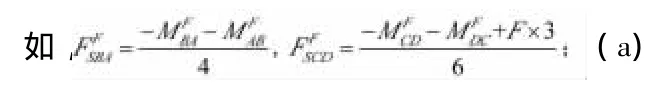
3.分层取脱离体,如图1(c)所示,由平衡条件计算因荷载而引起的附加链杆的反力R1F,

4.使基本体系的结点移动一位移Δ,确定各杆端由此引起的的杆端弯矩,并将它作为固端弯矩,再一次应用力矩分配法计算各杆端弯矩(设用MΔ表示);
5.重复步骤2与步骤3,确定某些杆的杆端剪力
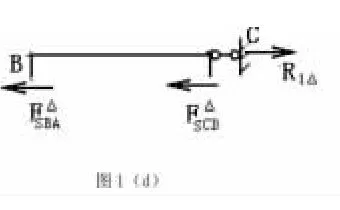
(设以SΔs表示),然后计算因Δ引起的附加链杆的反力 R1Δ(图 1d)。
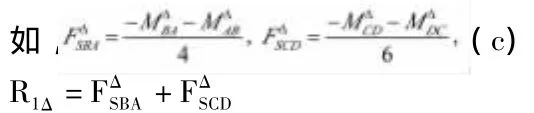
6.由位移法的基本方程:R1F+R1Δ=0(e)
解出位移Δ;
7.求得Δ后,原结构的最后弯矩可按叠加法求得:M=MF+MΔ。

三、“简便法”计算
对传统法中的具体步骤可进行整合如下:
首先,在步骤1、步骤4计算MF、MΔ时,二者其分配系数、传递系数各相同,所不同的只是各固端弯矩,因此将荷载及位移Δ
引起的固端弯矩共同作为其固端弯矩来进行分配、传递、叠加,以确定各杆端弯矩;杆端剪力FSF、FSΔ也不必按式(a)式(b)分别计算,而用计算得的杆端弯矩由平衡条件确定FS(因此FS=FSF+FSΔ)。
现对图1(a)所示的刚架进行具体计算。
1.计算各固端弯矩

2.计算各分配系数
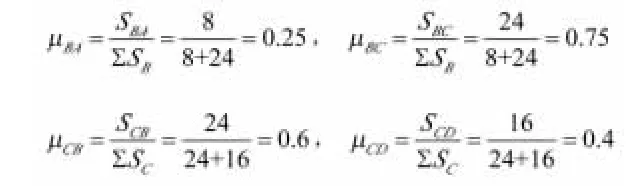
3.进行力矩分配、传递(见下表)

?
4.计算各杆端剪力

7.画弯矩图
根据以上求出的数值画出弯矩图,如图1(f)所示。
四、应用推广
上述实例题的仅仅是针对具有一个独立线位移的刚架而言的,同样对于具有两个及以上独立线位移的刚架,均可用类似的方法计算。

如图2(a)所示的刚架具有两个独立线位移Δ1、Δ2,则其固端弯矩MG由三个部分弯矩:MF、MΔ1、MΔ2组成的,由它进行分配、传递。相应需取两个分层脱离体,建立两个平衡条件:FSFGG+FSGCG-P1=0,FSDAG+FSEBG+
解联立方程求出Δ1、Δ2,最后将 Δ1、Δ2的值代入杆端弯矩,得到原结构的弯矩。
[1]梁圣复.建筑力学[M].北京:机械工业出版社,2007.
