矩阵的特征值与矩阵方程的关系

崔小琴,李虹晔

(湖北师范学院 数学与统计学院， 湖北 黄石 435002)

1 预备知识

矩阵特征值的研究是矩阵分析、微分方程、控制论等学科中的重要课题之一，许多文献对特征值的性质及求法都有所讨论,例如在[1]、[2]、[3]、[4]中作者分别介绍了一些特殊矩阵的特征值，如正交矩阵的特征多项式和特征根、三对角矩阵的特征值、分块矩阵特征值的分布以及3×3 矩阵的特征值问题等。本文在它们的基础上，借助于矩阵A与A*的方程，研究了A的特征值λ应满足的条件，并给出了一些特殊矩阵的特征值应满足的条件.

文章的第二部分是主要结果，第三部分给出了这些结果的一些应用.

为了证明的需要，给出以下两个引理.

引理1[5](Schur引理)给定A∈n×n，且λ1,λ2,……,λn是A的所有特征值，则存在一个酉矩阵U∈n×n，使得

U*AU=(tij)n×n

是上三角矩阵，且其对角线上的元素tii=λi(i=1,2,……,n) 是A的所有特征值，即

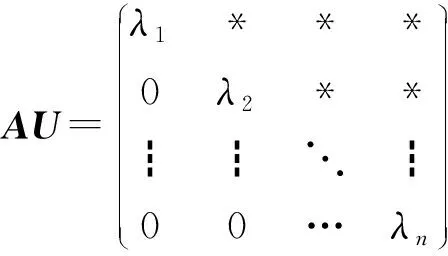
引理2 设A∈n×n，A的所有特征值为λ1,λ2,……,λn，f(x)∈[x] ，则

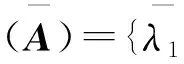
2)ρ(f(A))={f(λ1),f(λ2),……,f(λn)}.

证明 1)因为A与AT有相同的特征值，所以ρ(AT)=ρ(A) .由Schur 引理，存在酉矩阵U∈n×n使得

则

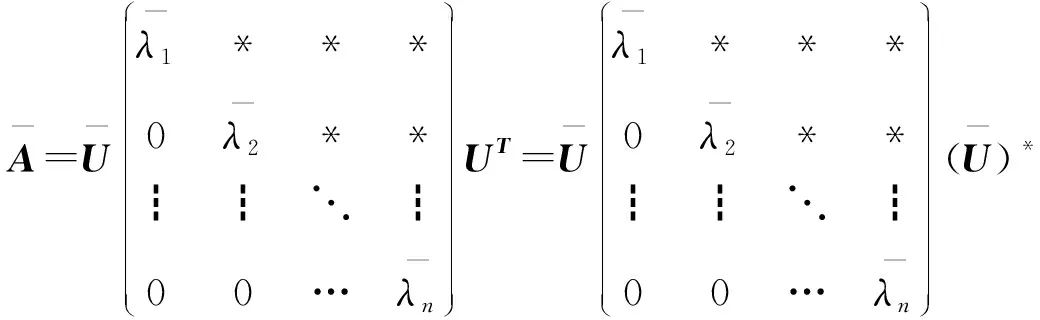
即

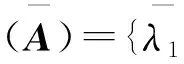
又因为转置不改变矩阵的特征值，所以

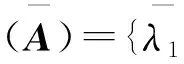
2)已知f(x)∈[x]，则f(A)有如下形式：

用Schur 引理得

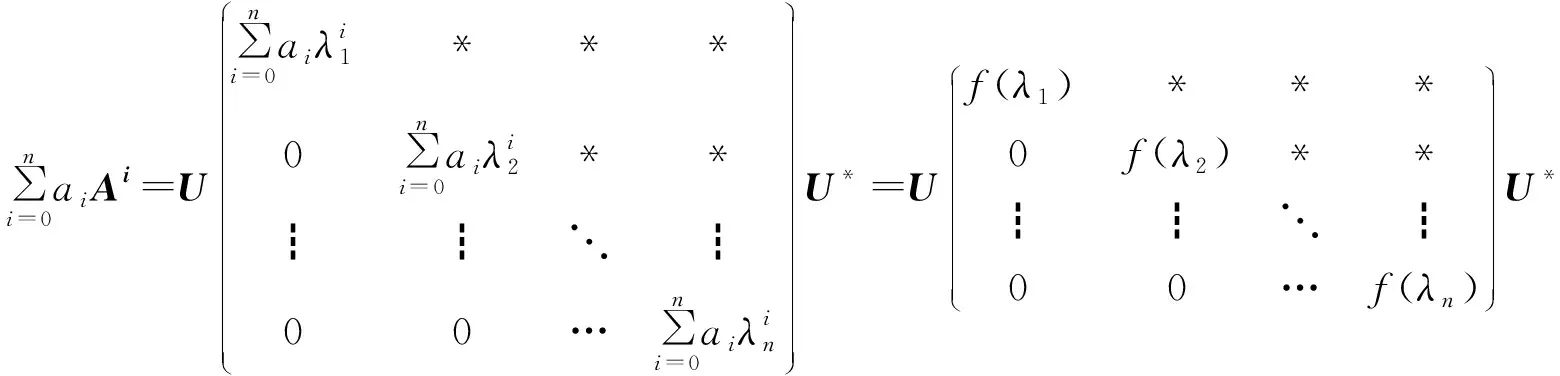
所以

ρ(f(A))={f(λ1),f(λ2),……,f(λn)}

2 主要结果

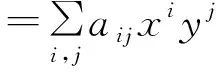
定理1 设A∈n×n，f(A*，A)=0,若λ是A的特征值,则,λ)=0.

证明 设α∈n是A的特征值λ所对应的特征向量，则有

Aα=λα

(1)

两边共轭转置得

(2)

因为

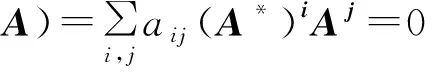
将该等式两边分别左乘α*，右乘α得

(3)

对上式反复用(1)和(2)可得出

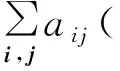
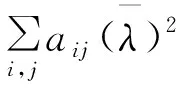
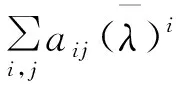
因为α为A的特征值λ所对应的特征向量,α≠0,α*α>0，因此有

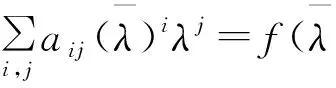
在定理1中，若将f(A*,A)=0中的A与A*交换位置，则结论也随之发生变化，这表明f(A*,A)中的A与A*的位置不能随意交换，所得的结论及证明将在下面给出.

定理2 设A∈n×n，f(A,A*)=0 ，若λ是A的特征值，则f(λ,

证明 因为A=(A*)*,所以

f(A,A*)=f((A*)*,A*)=0

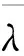
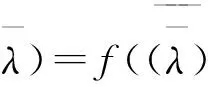
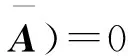
定理3 设A∈n×n，,AT)=0 ，若λ是A的特征值,则,λ)=0

f((AT)*,AT)=0

即

那么由引理2和定理1得出

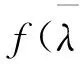
定理4 设A∈n×n，f(AT,，若λ是A的特征值,则f(λ,.

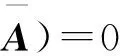
f(AT,(AT)*)=0

即

那么由引理2和定理2得出

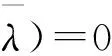
现在，我们将上述这些定理运用到一些特殊矩阵特征值的研究当中，如Hermit矩阵(A=A*)，反Hermit 矩阵(A=-A*)，酉矩阵(AA*=A*A=I)等.

推论1 Hermit矩阵的特征值为实数；反Hermit矩阵的特征值为0或纯虚数.

证明 设A为Hermit 矩阵，则有

f(A*,A)=A*-A=0

若λ是A的特征值，则有

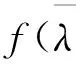
故λ为实数.

同理可得反Hermit 矩阵的特征值λ满足

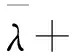
故其特征值为0 或纯虚数.

推论2 酉矩阵的特征值的模为1.

证明 设A为酉矩阵，则有

f(A*,A)=A*A-I=A*A-A0=0或f(A,A*)=AA*-I=AA*-A0=0

若λ是A的特征值，则有

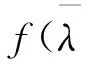
故|λ|=1 .

推论3 设A∈n×n,f(x)∈[x],f(A)=0,若λ是A的特征值，则f(λ)=0 .

证明f(x)∈[x] ,f(x) 可看成f(x,1) ，由定理1，f(λ)=f(λ,1)=0 .

3 应用

1997年， Groβ和 Trenkler在[9]中首先提出了关于广义投影算子和超广义投影算子的概念，并对这两类算子进行了研究.2004年到2005年，文献[10]和[11]中的作者讨论了广义投影算子和超广义投影算子的进一步性质以及广义投影算子的谱分解理论，接下来的一年， Stewart G W于文献[12]中利用谱分解理论刻划了广义投影算子，并给出了其分解式.2007年，文献[13]中作者讨论了k-广义投影算子.2008年， Jerzy K,Oskar Maria Baksalary和Liu Xiaoji于文献[14]中给出了广义投影算子和超广义投影算子的更深一层的结论.2013年，[15]中作者研究了可换的广义投影算子和超广义投影算子和与差的可逆性.下面，我们将结合以上定理对其分解式进行讨论并给出它的一个充要条件.

定理5A∈GP当且仅当A3=A*A=AA*.

证明 首先给出A∈GP的分解式.因为A∈GP,A2=A*, 若设λ是A的特征值，由定理1，有

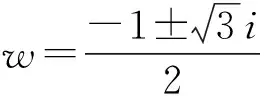
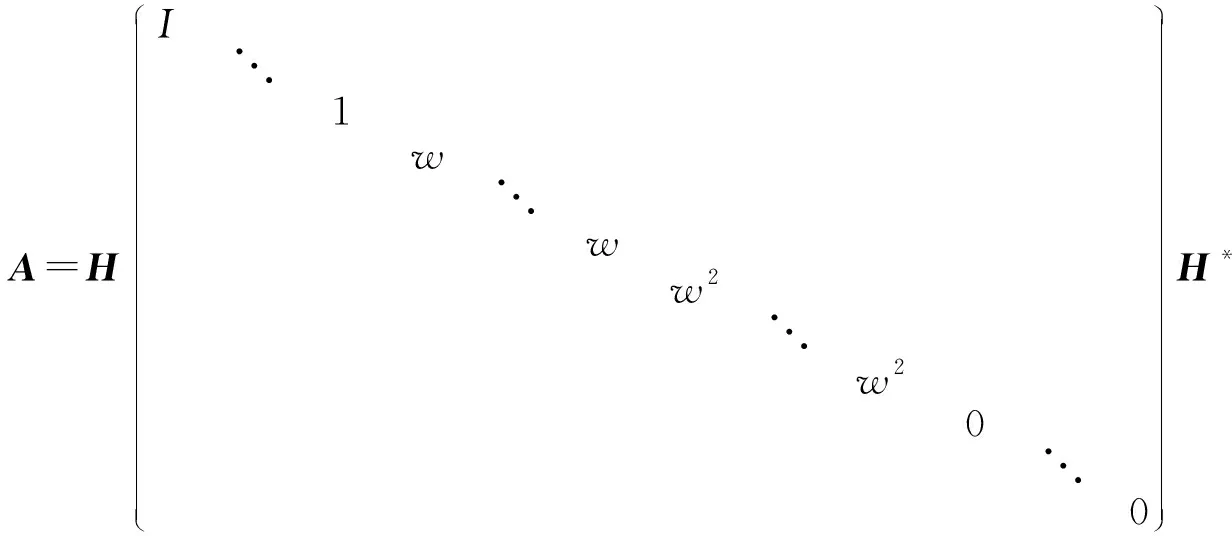
(4)

反之，若A有如(1)的分解式，则

所以A是广义投影算子当且仅当A有如(4)这样的分解式.

下面证明A∈GP当且仅当A3=A*A=AA*.

必要性易证.

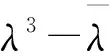
参考文献:

[1]张德菊，张晓敏.正交矩阵的特征多项式及特征根[J].大学数学，2007,23(1)：151～154.

[2]杨胜良，马成业.一种三对角矩阵的特征值及其应用[J].大学数学，2009,25(6)：182～187.

[3]Li zhuxiang,Pang Mingxian.The distribution of eigenvalues for partitioned matrix[J].Northeast Math J,1996,12(4):455～460.

[4]Geng Xianguo,Dai H H.Nonlinearization of the 3×3 matrix eigenvalue problem related to coupled nonlinear Schrodinger equations[J].Journal of Mathematical Analysis and Applications,1999,233(1):26～55.

[5]Horn R A,Johnson C R.Matrix Analysis(2)[M].Beijing:The people's posts and Telecommunications Press,2005:75～76.

[6]北京大学数学几何与代数教研室代数小组.高等代数[M].北京：高等教育出版社,1984.

[7]Franklin J N.Matrix theory[M].Englewood Cliffs,New Jersey:Prentice Hall,1968.

[8]Afrait S N.Orthogonal and oblique projectors and the characteristics of pairs of vector spaces[J].Cambridge Philosophical Society,1957,53(4):800～816.

[9]GroB J,Trenkler G.Generalized and hypergeneralized projectors[J].Linear Algebra Appl.264(1997):463～474.

[10]Baksalary J,Baksalary O,Liu X.Further properties of generalized and hypergeneralized projections[J].Linear Algebra Appl,2004,389:295～303.

[11]Du Hong-Re,Li Yuan.The spectral characterization of generalized projections[J].Linear Algebra Appl,2005,1(400):313～319.

[12]Stewart G W.A note on generalized and hypergeneralized projectors[J].Linear Algebra and its Applications,2006,412(2):408～411.

[13]Leila Lebtahi,Nestor Thome.A note on k -generalized projections[J].Linear Algebra and its Applications,2007,420:572～575.

[14]Jerzy K Baksalary,Oskar Maria Baksalary,Liu Xiaoji,et al.Further results on generalized and hypergeneralized projectors[J].Linear Algebra and its Applications,2008,429(5):1038～1050.