基于Modelica的光刻机超精密工件台建模与仿真

陈鹏飞， 王彦伟

(华中科技大学国家CAD支撑软件工程技术研究中心， 湖北 武汉 430074)

超精密工件台系统是光刻机的核心部件之一，具有定位精度高、响应速度快、动态性能好等特点[1-3]．文献[4]采用Matlab和Adams联合仿真的方法分析工件台的振动特性，并对工件台进行轨迹规划，取得较好的分析结果．由于需要将Adams中的数据转换到Matlab中，过程繁琐容易造成数据丢失．传统仿真大都基于某一特定领域软件，只能有效应对某单一领域的建模仿真．鉴于此，为了更加完整地仿真分析工件台系统，多领域仿真技术就显得尤为重要．Modelica语言采用面向对象的建模思想可以对耦合有机械、控制、电气、热、流体等多个领域的复杂产品进行物理建模和仿真分析[5]．本文采用Modelica语言对工件台系统进行多领域统一建模和仿真：首先给出了直线电机、控制以及工件台的数学模型；再基于这些子模型搭建工件台系统的Modelica多领域仿真模型；最后给定参数，对工件台进行仿真分析．

1 永磁同步直线电机建模

永磁同步直线电机(permanent magnetic linear synchronous motors,PMLSM)因其响应快、直接驱动的特点广泛应用于各种精密、超精密加工设备中．本文所研究的光刻机超精密工件台系统就采用PMLSM作为驱动工件台部分的执行机构．鉴于PMLSM的强耦合性和非线性，为了便于分析，将电机方程按照统一电机理论作线性变换，实现耦合方程的解耦．建立在d-q轴坐标系下的PMLSM数学模型[6]如下：

电磁推力方程

电机机械运动方程

Fe=mpv+Bv+Fl．

上述各式中：ud，uq，id，iq，ψd，ψq，Ld，Lq分别表示永磁同步直线电机d轴和q轴的电压，电流，磁链，电感；Rs表示PMLSM的定子电阻；p为微分算子，p=d/dt；ω为PMLSM直线速度折合成的等效旋转电机角速度，ω=πv/τ；v为动子的运动速度；τ为极距；P为电机的极对数；Fe为电磁推力，Kt为推力常数；Fl为负载阻力；B为与速度相关的粘滞系数；m为电机运动部分的质量，包括动子以及动子所带动负载的质量．

2 工件台动力学建模

光刻工件台采用的是H型结构，由水平向X导轨和水平向Y1Y2导轨组成，可以实现X、Y和θz三个自由度的运动．X向电机的动子与曝光卡盘固接构成了微动台，当微动台发生微小转动时，可以获得微动台上的坐标原点(加工点)与微动台的质心之间的关系[7]．令微动台的质量为M(包括直线电机动子质量)，绕质心处转动惯量为J,对微动台进行受力分析，最终得到工件台动力学模型：

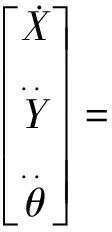
式中：FX,FY1,FY2分别是直线电机X,Y1,Y2的实际驱动力；L1和L2分别为Y1,Y2电机动子质心到工件台质心的距离．

3 控制系统建模

为了能够进行高精度、高速度的运动，工件台除了需要进行准确的动力学建模外，还必须有相应的控制策略．本文基于空间矢量脉宽调制(space vector pulse width modulation,SVPWM)控制策略，采用位置环、速度环、电流环的三闭环控制方案．为了提高系统性能位置环采用PID调节器，速度环和电流环则分别采用PI调节器．由于光刻机在工作时，上位机发给工件台的指令是精密工件台的X,Y,θz三个方向的位置，而工件台驱动电机输出的是三个电机的位置，所以在对工件台进行控制前需要对其驱动电机进行坐标变换．根据以上分析搭建控制领域的Modelica模型如图1所示.

图 1 控制系统Modelica模型

4 工件台系统多领域模型的建立

根据以上对光刻机精密工件台各个子模型的分析，采用基于Modelica的建模方式建立光刻机精密工件台仿真模型库，主要包括永磁同步直线电机模型、工件台动力学模型、PID控制器模型、空间矢量脉宽调制模型、逆变器模型、理想电源模型等子模型．根据模块化的思想在Mworks仿真平台上采用组件连接的方式将各子模型连接构成光刻机超精密工件台的参数化多领域仿真模型．该模型是机械、电气、控制的耦合体．为简便起见，只给出工件台X向运动系统图，最终模型如图2所示．

5 仿真结果分析

在仿真实验中采用交流永磁同步直线电机参数P=2，Rs=10 Ω，Ld=Lq=0.01 H，ψf=0.5 Wb，m=10 kg，τ=0.01 m，空间矢量脉宽调制频率f=10 000 Hz，电压Udc=50 V．速度控制器的系数Kspeed=200，Tspeed=2；d轴和q轴方向电流控制器的系数分别为Kd=200,Td=0.5,Kq=150,Tq=0.5；位置PID控制器的系数分别为Kposition=300,Tip=10，Tdp=0.0005．输入不同信号进行试验，X向电机对位移为S型曲线和阶跃信号的响应分别如图3和图4所示．由图3可以看出X向轨迹跟踪稳态误差可以达到纳米级精度．对比图3和图4可以看出工件台对不同轨迹的响应，其运动精度是不同的．因此，设计出合理的超精密工件台运动轨迹算法对于提高光刻机的运动精度、加工精度和运行效率具有十分重要的意义．

图 2 工件台X向控制模型

图 3 X向电机位移的S型曲线响应

图 4 X向电机位移的阶跃响应

6 结束语

本文采用面向对象的物理建模语言Modelica，建立了包含控制、电气及机械领域的光刻机超精密工件台多领域仿真模型库．该模型保留了工件台的多领域结构属性，具有良好的模型重用性，可以用于对工件台进行多领域耦合分析以及轨迹规划算法的比较分析．

[参考文献]

[1] 朱 煜,尹文生,段广洪.光刻机超精密工件台研究[J].电子工业专用设备,2004,(109):25-27.

[2] 汪劲松.我国“十五”期间IC制造装备的发展战略研究[J].机器人技术与应用,2002(1):5-9.

[3] 董吉洪,田兴志,李志来，等.100nm步进扫描光刻机工件台、掩模台的发展[J].光机电信息,2004,(5):20-24.

[4] 鲍秀兰.光刻机精密气浮工件台振动特性分析及运动控制[D].武汉:华中科技大学图书馆,2007.

[5] 赵建军,丁建完,周凡利，等.Modelica语言及其多领域统一建模与仿真机理[J].系统仿真学报,2006,18(2):570-573.

[6] 金建勋,郑陆海.基于SVPWM的永磁同步直线电机模型仿真[J].智能系统学报,2009,4(3):251-257.

[7] 縢 伟,高青风,武 鑫,等.超精密工作台多自由度运动控制[C]//中国自动化学会控制理论专业委员会，第三十届中国控制会议,山东烟台，2011．