锚杆中纵向超声导波传播特性数值模拟研究
2013-11-13孙晓云赵冬松刘东辉于健骐
孙晓云,赵冬松,刘东辉,于健骐
(1.石家庄铁道大学电气学院,河北石家庄 050043;2.河北科技大学电气工程学院,河北石家庄 050018;3.中国环境管理干部学院信息工程系,河北秦皇岛 066004)
锚杆锚固技术广泛应用于各类地下硐室、边坡治理等工程的加固补强效果中,是目前各类地下工程十分重要的一项技术之一,它的主要技术措施是喷锚支护,对岩土体的利用、整治和改造中,能有效控制岩土体的稳定性,使之具有服务功能的加固技术的总称。与此同时,锚杆锚固质量的检测技术成为目前工程中迫切需要解决的问题。拉拔实验作为锚杆传统的检测手段虽然直观,但操作过程复杂,对锚固系统也是破坏性的,只限于抽检。目前的无损检测技术大都基于一维锚杆波动理论,通过收集接收到的弹性反射波的时域与频域信息,对锚杆锚固质量进行检测[1]。目前,中国应用导波对锚杆锚固质量的检测的研究还处于起步阶段。
1 导波的传播速度
导波不同于一般的体波,在无限均匀介质中传播的波叫做体波,纵波(P波)和横波(S波)是体波传播的2种基本形式,由于其远离边界,不会发生波形转换,它们都以各自的特征速度向前传播,而无波形耦合。导波是波在波导介质中的传播,它受介质边界条件的影响,当波传播到边界处,会以反射和折射的形式发生相互作用,且会发生纵、横波之间的相互转换,各种类型的反射、折射波会以各自恒定的速度继续向前传播,其传播的波速只与材料的弹性模量和密度相关[2]。当固体弹性介质具有多个边界时,波在介质中会发生复杂的干涉,并按一定规律依次向前推进,波的这种传播方式叫做导波。锚杆及其锚固结构是一个圆形柱体结构,其直径为15~35 mm,对锚杆检测时激振波频率一般为10~100 kHz[3],所以在锚杆中传播的波必然为一个导波,在柱体中传播的导波叫做柱面导波,它具有3种模态纵向L(0,m)、扭转模态T(0,m)、弯曲模态F(n,m)。其中n表示导波绕轴向的传播形态,m表示导波沿杆径方向的振动形态[4-6]。导波在波导中的一个重要特性是多模态和频散特性[7-10],即不同频率导波传播的速度和衰减性不同,描述导波传播速度的2个基本概念是导波的群速度和相速度。群速度是指波包络的传播速度,相速度是指波上相位相同的一点传播的速度,它们的定义分别为[11]
cg=dω/dk,
(1)
cp=ω/k,
(2)
式中:k为圆波数;ω为圆频率。
它们两者之间的关系为
(3)
式中:f为导波的频率;d为圆柱的半径;fd称为频厚积。
工程上一般采用低频的纵向模态导波对锚杆进行质量检测,本文将锚杆作为波导,用数值模拟方法研究纵向模态导波在锚杆中的传播特性。
2 波在实心自由圆杆中纵向传播模态
对于无限长自由状态的圆杆,外边界处的应力为零,边界条件为
σrr=σrz=0,(r=R)。
(4)
纵向导波在无限长圆杆中传播的频散方程为[12]
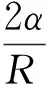
(5)
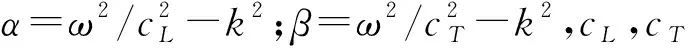
首先对方程(5)进行变换,两端同时乘以R4,可以得到:
2Rα(R2β2+R2k2)J1(Rα)J1(Rβ)-(R2β2-R2k2)2J0(Rα)J1(Rβ)-4R2k2RαRβJ1(Rα)J0(Rβ)=0。
(6)
将固体材料的纵、横波波速(其表达式如式(7)所示)带入式(6),令ω=2πf,便可得到关于fR和kR之间关系的频散方程:
(7)
式中:υ为泊松比;ρ为材料密度。
方程中的2个未知数隐含在频散方程中,利用Matlab通过数值方法对其进行求解。其求解过程如下。
1)首先令kR=0,在0~5 MHz·mm范围内搜索满足方程的fR的值,频散关系中这些频率值为各个纵波模态的截止频率。
2)以横轴上各个截止频率处作为起点,增加1个fR步长值,并向上搜索kR直到满足频散方程,将其保存到数组中,然后令fR再次增加1个步长,纵向用上次搜索到的kR值作为起点继续向上搜索,依此类推,直到搜索完所要求解的范围。
锚杆材料参数如表1所示[14],基于以上方法求解了频厚积在0~5 000 kHz·mm内纵波的频散曲线,图1为波数半径积与频厚积之间的关系,图中各曲线从左至右依次为杆中纵波的L(0,1)~L(0,4)模态,除了第二阶模态的变化趋势有些异常外,其余

表1 锚杆材料参数Tab.1 Material parameters
导波都有相同的变化趋势,其中除了L(0,1)之外,其余模态都有截止频率。
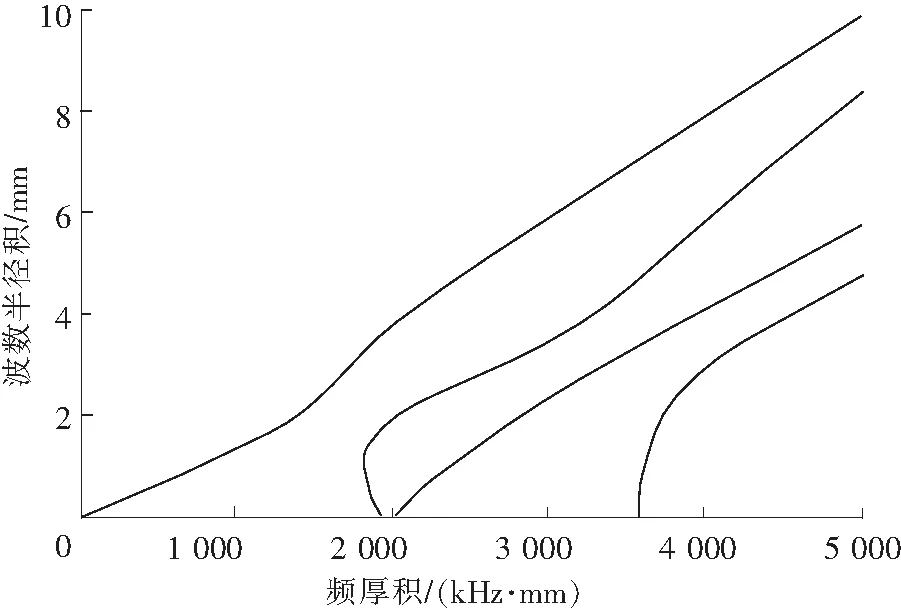
图1 波数半径积与频厚积之间的关系Fig.1 Relationship between the wave number and frequency
相速度和群速度的求解分别按照式(2)和式(3)对各阶模态进行求解,结果如图2和图3所示,从相速度频散曲线上可以看出当fR→0时,L(0,1)模态的相速度趋近于纵波波速,并且在0~1 800 kHz·mm的范围内只存在一种纵向模态导波,对于杆直经约为20 mm的锚杆,在0~180 kHz之间存在一种纵向模态导波。所有的纵向模态导波中,当频厚积fR→∞,一阶纵向模态导波的相速度趋近于Rayleigh波速度也即纵波在杆中传播的波速,而较高阶模态的相速度趋近于cT。对比各相速度和群速度曲线可以看出一般情况下各相速度都要大于群速度。
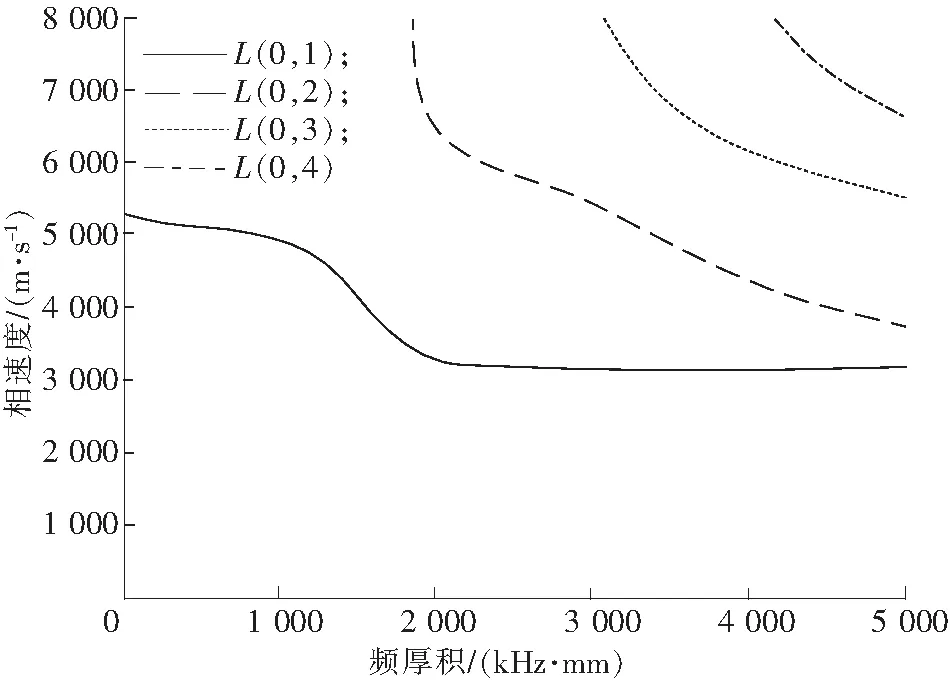
图2 相速度与频厚积之间的关系Fig.2 Relationship between the phase velocity and frequency
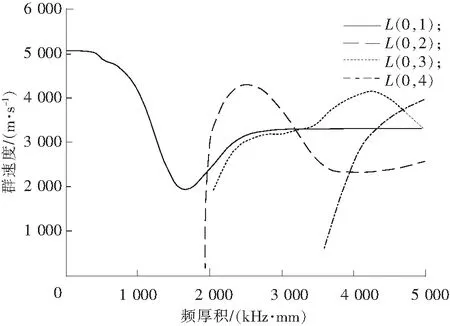
图3 群速度与频厚积之间的关系Fig.3 Relationship between the group velocity and frequency thick plot
对于每条kR曲线,某一频率的纵向导波在柱面坐标系中随时间变化的位移场的分布如式(8)所示[12]:
(8)
式中Dn为未知常数。
对于半径约为10 mm的锚杆,图4所示为50 kHz时锚杆中传播的一阶纵向导波位移模式沿半径的分布情况。
3 锚杆中纵向导波数值模拟
3.1 不同频率导波在锚杆中的传播特性
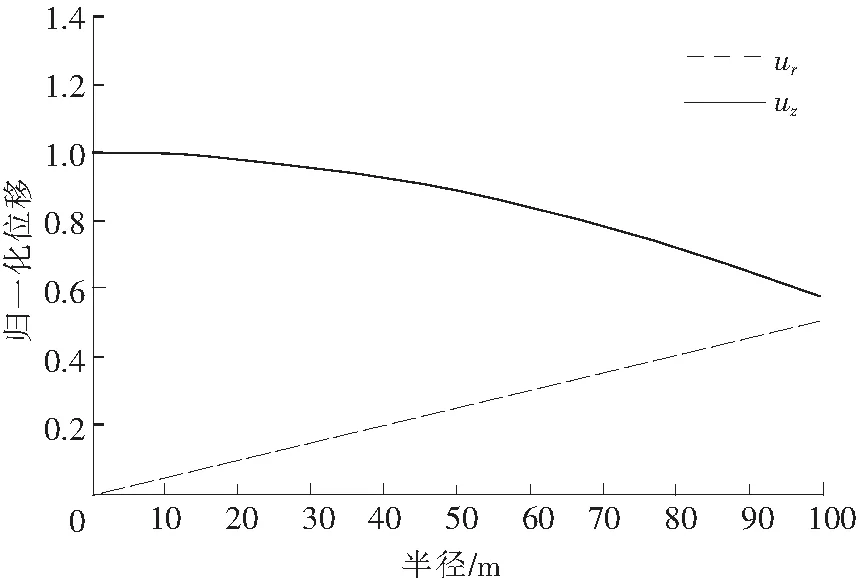
图4 一阶纵向模态轴向位移分布Fig.4 Displacement distribution of the first-order longitudinal modes
利用Dyna进行有限元数值模拟,本实验利用Dyna的显式分析单元Soild164,材料模型为各向同性线弹性材料模拟了长为2 m、直径为0.02 m的锚杆中不同频率导波传播特性。有限元模型共划分了27 000个单元,30 371个节点,其中对模型底端节点施加全约束,材料模型并不考虑材料本身阻尼对导波的影响,本文在此只做几何频散研究,图5为在顶端施加激振频率为30~90 kHz时,锚杆顶端的时域响应曲线。为了保证波包的激振宽度,不同频率施加的激励波周数不同。
从频散曲线中可以看到低频状态下锚杆中只存在一阶纵向模态导波,从图5中可以看到导波在60 kHz时开始有明显的衰减现象,90 kHz时几乎看不到第2个反射波包,波包能量衰减严重。表2为第一反射波包和第二反射波包峰值点的大小。
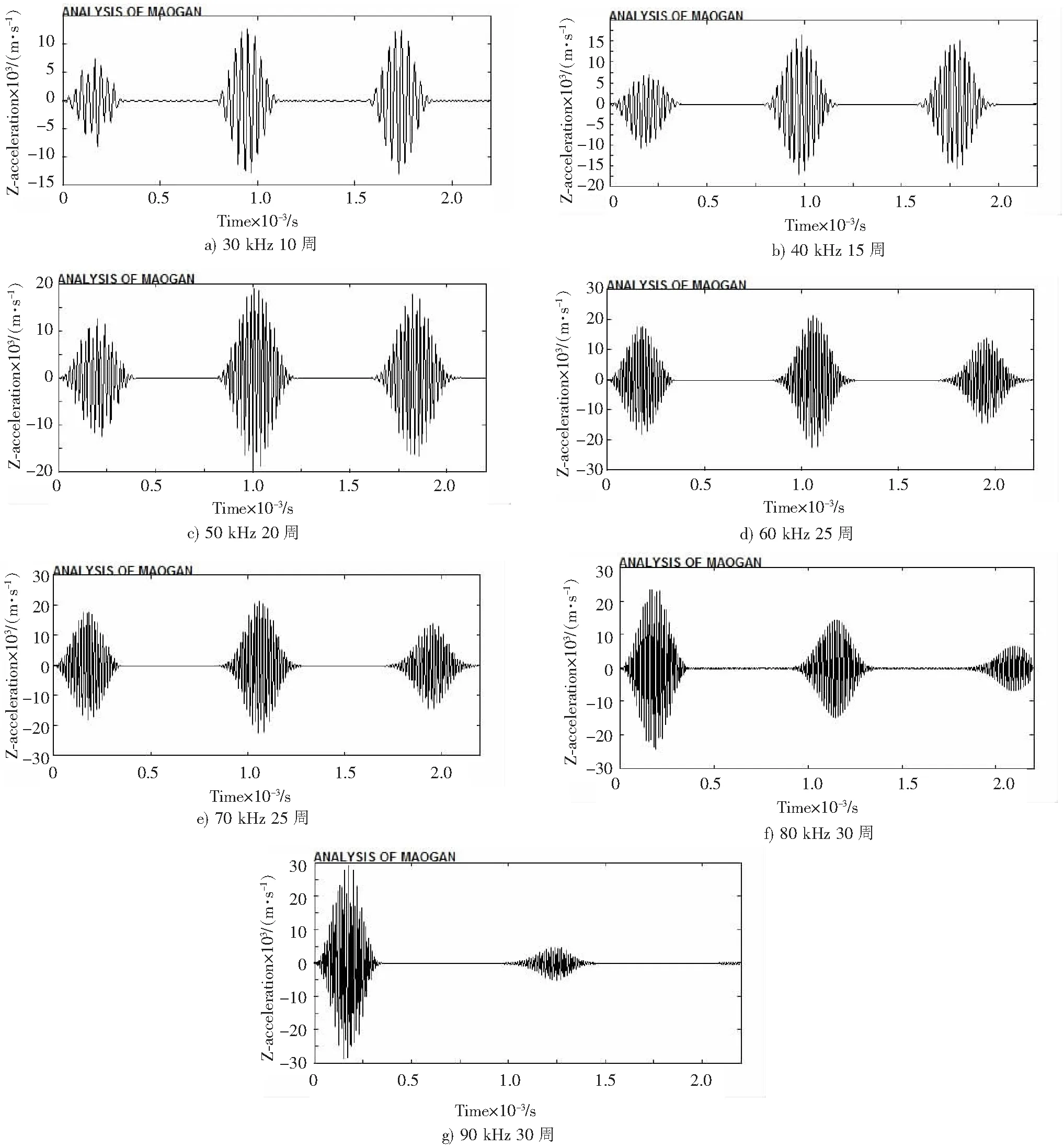
图5 一阶低频纵向导波在锚杆中传播特性Fig.5 Propagation characteristics of the low-frequency first-order longitudinal guided wave in the bolt
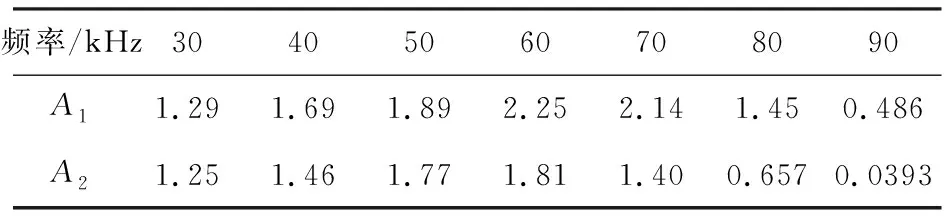
表2 第一反射波包峰值A1和第二反射波包峰值A2Tab.2 Amplitude of the first wave packet A1 and the second wave packet A2
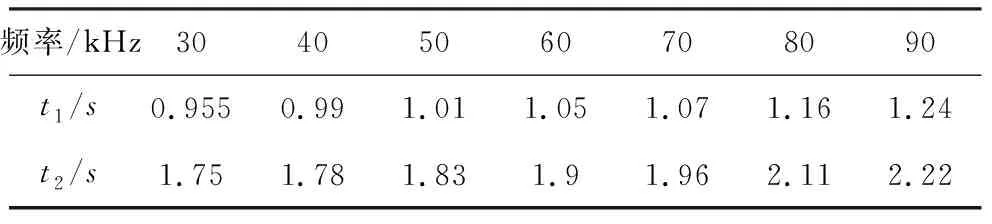
表3 第一波包和第二波包峰值点反射时间Tab.3 Reflection time of the first wave packet and the second wave packet
定义第一反射波包和第二反射波包幅值之比为[15]
(9)
各频率导波波包峰值衰减如图6所示。
表3为第一反射波包峰值点和第二反射波包峰值点到达杆顶的时间t1和t2。
群速度为
(10)
与频散曲线理论值对比如图7所示。
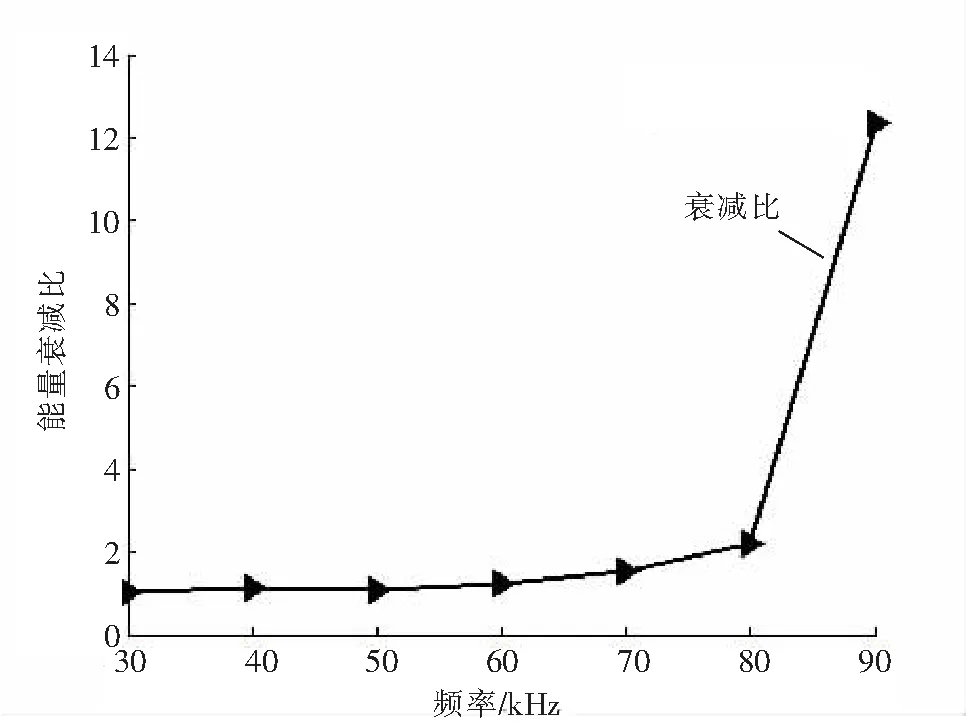
图6 波包峰值衰减比Fig.6 Wave packet amplitude attenuation ratio
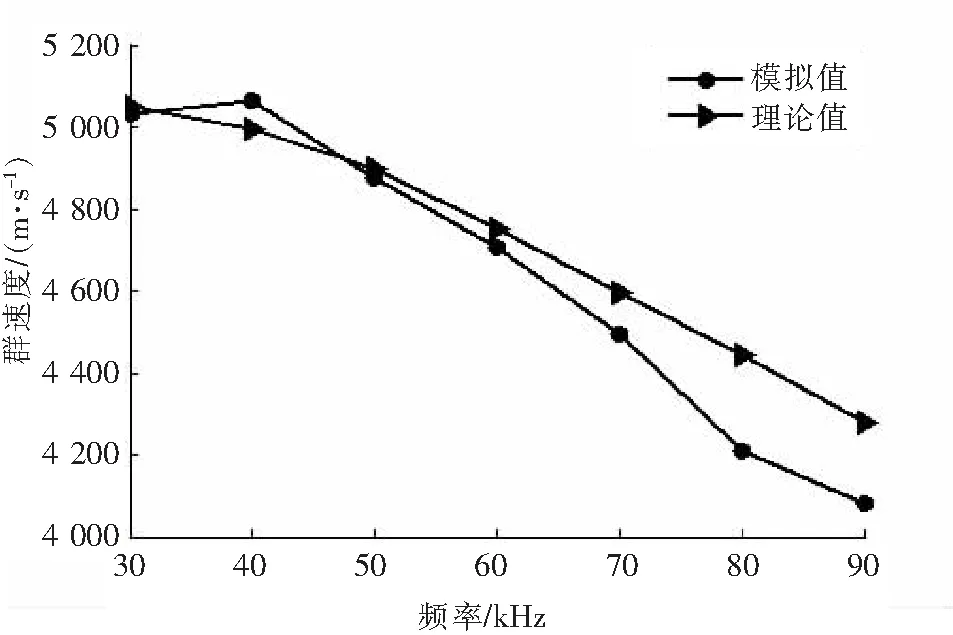
图7 理论速度与模拟速度对比Fig.7 Contrast of theoretical velocity and analog velocity
3.2 杆顶三维效应对锚杆检测的影响
利用LS-Dyna模拟了30 kHz超声导波在无锚固直径为38 mm,长为1 m的锚杆中传播时顶端的三维效应。分别对杆顶截面中心和边缘部位施加集中激振力载荷如图8所示,在集中激振力载荷作用下,杆顶截面已不再符合平截面假设,杆顶各处质点在激振时各处加速度不一致。
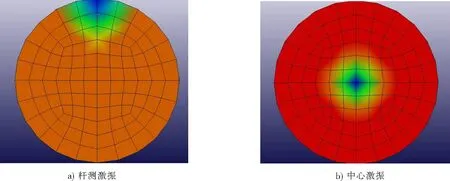
图8 2种激振方式顶端应力分布Fig.8 Stress distribution at the top in two exciting way
图9为锚杆顶端从上到下各点处接收到的曲线三维效果图,从杆侧激振时各处接收到的时域波形中可以看出在杆顶靠近边缘处的波形成分较多,杆顶中心处,接收到的波形几乎不受影响,在应用导波检测时,应尽量将传感器安设在杆顶中心位置处,以免截面上各点的振动情况不一致,对检测结果造成影响。
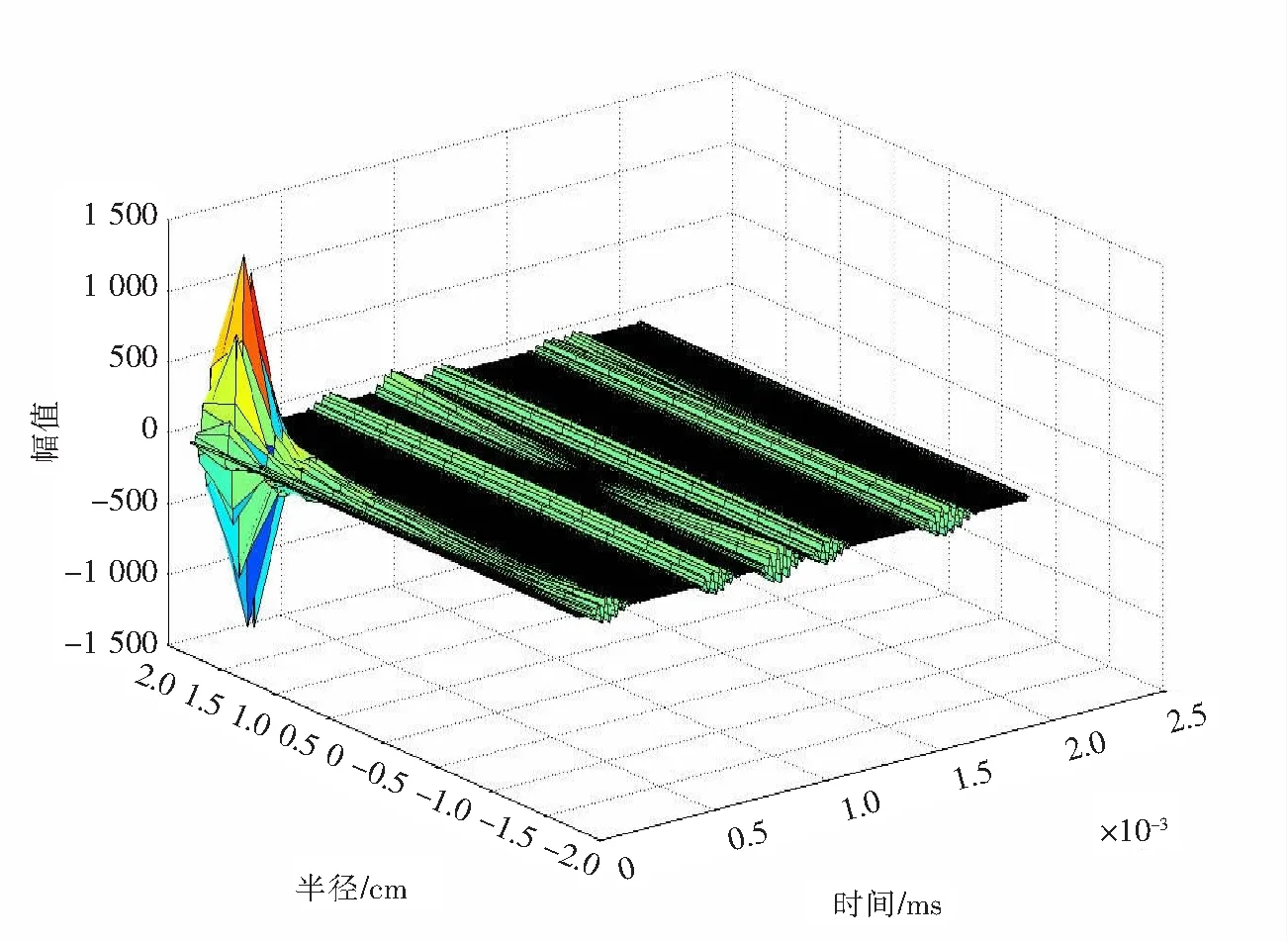
图9 杆侧激振时顶端时域响应曲线Fig.9 Time domain response curve of exciting way in the side of the bolt’s top
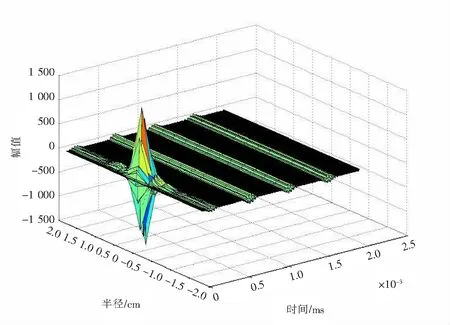
图10 中心激振时顶端时域响应曲线Fig.10 Time domain response curve of exciting way at the middle of the bolt’s top
图10为在杆顶中心处施加激励载荷,杆顶各点随时间变化的响应波形曲线,在激振最初,由于杆顶各处应力分布不均,在中心处质点加速度最大,并且边缘处质点的加速度曲线相位滞后于中心质点,但在反射回波中,各处质点振动回复一致,当波在传播一段距离后,可以认为平截面假设成立,所以激振设备在杆顶激振时应尽量施加对称分布的载荷。
4 结 语
1) 通过理论分析和数值模拟表明锚杆中的声波是以导波形式传播的,并且在达到一定频率后,锚杆中的纵向导波会存在多种模态,对于直径约为0.02 m的锚杆,在0~180 kHz之间,只存在一种导波模态,但在90 kHz附近波包能量衰减严重,在利用导波测长时,应结合各频率波速,才能得到可靠的结果。
2) 利用导波检测大直径锚杆时,应将换能器安装在杆顶中心处,以免杆顶三维效应对检测结果造成影响。
参考文献/References:
[1] 孙晓云, 杨 阳. 基于ARM & Windows CE的锚杆无损检测系统软件设计[J]. 河北科技大学学报, 2012,33(3):244-247.
SUN Xiaoyun, YANG Yang. Software design of non-destructive detecting of rock bolts based on ARM & Windows CE[J]. Journal of Hebei University of Science and Technology, 2012,33(3):244-247.
[2] 吴 斌, 李隆涛, 王秀彦, 等. 基于超声导波技术对钢杆表面缺陷的无损检测研究[J]. 工程力学,2006,20(5): 149-154.
WU Bin, LI Longtao, WANG Xiuyan, et al.Non-destructive test of a surface defect on a steel bar based on ultrasonic guided wave techniques[J]. Engineering Mechanics, 2006, 20(5):149-154.
[3] 李 平, 高德政, 陈兴长. 自由锚杆中超声导波的最优激发波研究[J]. 西南科技大学学报, 2009,24(3):50-54.
LI Ping, GAO Dezheng, CHEN Xingchang. Study on optimum excitation wave of ultrasonic guided wave in free rock bolt [J]. Journal of Southwest University o f Science and Technology, 2009,24(3):50-54.
[4] 何存富, 孙雅欣. 超声导波技术在埋地锚杆检测中的应用研究[J]. 岩土工程学报, 2006, 28(9):1 144-1 147.
HE Cunfu, SUN Yaxin. Application of ultrasonic guided waves technology to inspection of bolt embedded in soils[J]. Chinese Journal of Geotechnical Engineerin, 2006,28(9):1 144-1 147.
[5] 崔寒茵. 沿均匀无限介质中固体杆传波的导波特性研究[J]. 声学学报, 2010,35(4):446-454.
CUI Hanyin. Guided waves in a rod surrounded by an infinite soild medium[J]. Acta Acustica, 2010,35(4):446-454.
[6] BEARD M D, LOWE M J S. Nondestructive testing of rock bolts using guided ultrasonic waves [J]. International Journal of Rock Mechanics & Mining Sciences, 2003, 40(10):527-536.
[7] 王 成. 金属杆锚固系统中导波传播特性的试验研究[J]. 无损检测,2006,28(4):172-176.
WANG Cheng. Experimental study on the propagation characteristices of guided wave through anchored system of metal bar[J]. Nondestructive Testing,2006,28(4):172-176.
[8] 孙广开, 焦 阳. 超声导波管道缺陷检测数值模拟[J]. 河北工业科技, 2010,27(1):18-21.
SUN Guangkai, JIAO Yang. Numerical simulation of detection in pipes using ultrasonic guided waves[J]. Hebei Journal of Industrial Science and Technology, 2010,27(1):18-21.
[9] 梁玉国. 无机锚固材料植筋群锚效应试验研究[J]. 河北工业科技, 2013,30(1):31-34.
LIANG Yuguo. Experimental research of anchor group effect in post-embedding technology by inorganic anchoring material[J]. Hebei Journal of Industrial Science and Technology, 2013,30(1):31-34.
[10] 陈兴长. 自由锚杆中超声导波的衰减特征[J]. 西南科技大学学报, 2009,24(4):56-61.
CHEN Xingchang. Attenuation characteristics of ultrasonic guided wave in free rock bolts[J]. Journal of Southwest University of Science and Technology, 2009,24(4):56-61
[11] 岳向红. 基于三维波导理论的基桩和锚杆无损检测技术研究[D]. 武汉:中国科学院武汉岩土力学研究所, 2008.
YUE Xianghong. Research of Pile and Bolt’s Non-destructive Test Technology Based on 3D Guided-wave Theory[D]. Wuhan:Institute of Rock & Soil Mechanics, The Chinese Academy of Seiences, 2008.
[12] 罗斯J L. 固体中的超声波[M].何存富, 吴 斌,译. 北京:科学出版社, 2004.
ROSE J L. Ultrasonic Waves in Solid Media[M].Translated by HE Cunfu, WU Bin. Beijing: Science Press, 2004.
[13] 刘增华, 赵继辰, 吴 斌,等.高阶纵向超声导波在钢绞线缺陷检测中的应用[J]. 工程力学, 2011,28(4):214-220.
LIU Zenghua, ZHAO Jichen, WU Bin, et al. Application study on defect detection in steel strands by using high-order ultras-onic longitudinal guided waves[J].Engineering Mechanics, 2011,28(4):214-220.
[14] 张昌锁, 李 义, STEVE Z. 锚杆锚固结构中导播传播的数值模拟[J]. 太原理工大学学报,2009,40(3):274-278.
ZHANG Changsuo, LI Yi, STEVE Z. Numerical simulation of guided wave propagation in grouted rockbolt[J]. Journal of Taiyuan University of Science and Technology, 2009,40(3):274-278.
[15] ZHANG C S, ZOU D H, ADENGA V M. Numerical simulation of wave propagation in grouted rock bolts and the effects of mesh density and wave frequency [J]. International Journal of Rock Mechanics & Mining Sciences, 2006(43):634-639.
