淮南矿区深部岩巷典型围岩参数反分析研究!

高 玮，刘泉声

（武汉大学 土木建筑工程学院，湖北 武汉 430072）

从20世纪末本世纪初开始，淮南矿区主要矿井相继开拓延伸到-700m 以深的深部.据2001年底的调查，当时新庄孜矿开拓延伸的深度已达到-812 m；谢桥矿达到-720 m；谢一矿达到-780m；潘三矿达到-812m；望峰岗矿达到-817m.可见，全矿区已整体进入了深部开采阶段［1］.进入深部开采后，由于岩石所处环境的变化，深部岩石巷道出现了一些不同于浅部的特征［2-3］，主要有：由于地应力升高，围岩内赋存的高地应力与其本身低强度之间的矛盾更加突出，巷道开挖后二次应力场引起的高度应力集中导致近表围岩受到的压剪应力超过围岩强度，围岩很快由表及里进入破裂碎胀和塑性扩容状态，极易出现大变形而整体失稳；随着采深的增加，地下水渗透压力相应增大，巷道开挖后近表围岩内孔隙水压力大幅降低，导致巷道近场围岩有效应力增大，致使围岩应力进一步超过岩体强度，从而加剧近表围岩的破坏失稳；随着开拓深度的增加，地温升高，巷道开挖后，由于通风在距离巷道表面一定深度围岩内产生较大的温度梯度和附加应力，使围岩产生离层，对围岩破裂扩展带来不可忽视的影响.但是实际工程中由于没有认识到深部巷道围岩与浅部巷道围岩在变形破坏上的根本差异，对深部巷道围岩的变形破裂机理缺乏深入认识，因此，尽管已经进入深部开采阶段，但整个矿区深部岩巷仍然普遍采用的浅部岩巷中的主要支护形式.由于这种认识上的不足，很多矿井的巷道一个月左右即出现严重大变形破坏而失稳，其主要表现为，由于两帮收敛变形过大而导致锚杆拉断、喷层严重折断破裂或U 形钢支架严重扭曲变形，巷道出现不同程度的底臌，底臌严重地段的底板隆起变形量达到1～2m.由于巷道接连不断的失稳破坏，各矿不得不投入大量精力进行巷道翻修，使得矿井生产运输受到严重影响、巷道维护成本大大增加，严重制约了整个矿区煤炭生产，降低了经济效益.为了从根本上解决淮南矿区深部岩巷的支护和围岩稳定控制的难题，清除煤炭生产运输的主要障碍，淮南矿业集团委托多家单位开展了系统的理论研究和技术攻关，试图找到深部岩巷围岩破坏的机理.进行围岩破坏机理的研究，围岩参数的确定是一个关键的问题，为了解决这个问题，本文基于现场试验中的大量位移实测资料，采用进化神经网络进行了典型围岩参数的反分析研究，试图为围岩破坏机理的研究提供必要的参数.

1 反分析方法简介

从系统论的观点看，工程反分析问题实质为一个逆系统的辨识问题［4］.其具体阐述为，在正分析中，已知系统的输入，求其输出；而在反分析中，已知系统的输出或部分输出，求其对应的输入.相对于正分析的运行系统，反分析所求解的为系统的逆模型.系统逆模型的辨识可形象地由图1所示.

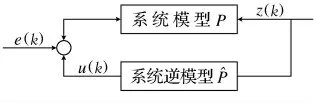
图1 系统逆模型的辨识Fig.1 Identification of system inverse model

定义

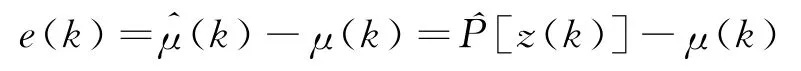
对于上式，如果可得到显式的解析表达式，则可采用矩阵求逆等方法解决此问题.这也就是传统的逆反分析的求解思路.而实际上，对于地下工程问题来说，由于其监测位移同围岩物性参数等间的关系非常复杂，根本不可能写出其显式解析表达，再加上监测位移一般均存在量测误差噪声，这更使得二者间的关系复杂化.因此，对于地下工程问题，采用矩阵求逆等方法是行不通的.可以设想如果能找到黑箱式模型来表达z（k）→＾μ（k）的关系，那么这个问题也就解决了.由此可以发现，神经网络模型恰好是这样一种黑箱式模型，它可以仅由一些已知样本来反映整个系统的模型.为了克服传统神经网络存在的难以克服的很多困难，这里采用进化神经网络进行研究.

神经网络的训练样本是网络训练成功的关键问题.样本的获取是建立神经网络模型的首要一步.因此，如何获取逆反分析神经网络模型的训练样本是我们要做的首要工作.由于反分析实质为一个逆系统的辨识问题，因此，关于神经网络样本的获取我们应该可以从系统辨识理论的描述中得到启发.

系统控制论中，逆系统辨识的过程可用图2来描述.由图2可见，逆系统辨识问题同系统正问题的计算可以是一个闭环系统.因此，逆系统辨识所需的信息可以来自系统正问题的计算结果.可见，逆反分析神经网络模型的样本很明显可以来自其正分析的计算结果.

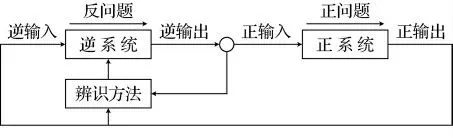
图2 逆系统辨识过程示意图Fig.2 Process of inverse system identification

理论分析可以知道要想得到一个逼近及泛化能力均较强的神经网络模型，网络训练样本的典型代表性是一个关键的问题，这就涉及到样本的质量及数量的问题.由于地下工程反分析神经网络模型的训练样本要依赖于相应的正问题的数值计算，而地下工程正问题数值计算是一个很耗时的过程，因而，对实际应用来说，样本的数量应越少越好.而同时样本的质量是网络训练成功的重要因素.因此，理想的情况就是样本的数量尽量少而其质量尽量高.把这种要求同地下工程神经网络反分析样本获取的正分析计算结合起来，则问题转化为在待反演参数的取值空间中选取代表点的问题.很显然，此问题就是一个实验设计问题，即如何选取实验范围（因素空间）中的代表点.

正交试验设计法是一种科学地安排与分析因素试验的方法.它依据正交性原则来挑选试验空间中的代表点.这种方法能大大减少试验次数，并具有“均衡分散性”及“整齐可比性”.因此，进化神经网络的训练样本集采用正交试验设计法进行选取.

为了得到尽可能好的反分析效果，这里采用一种新的进化神经网络模型.该模型融合了免疫进化规划及传统BP 神经网络的优点，实现了效率和效果的最佳结合，该进化神经网络的基本流程见图3.具体方法为，根据工程逆反分析的要求，进化神经网络逆反分析的目的就是由预先得到的位移同参数关系的样本集对进化神经网络进行训练最终得到反映位移同参数间的复杂映射关系的最佳神经网络结构及其连接权值，则此神经网络模型就反映了位移同参数间的复杂非线性关系.具体反分析时，把现场观测位移输入该神经网络模型，则会得到其相应的参数输出.

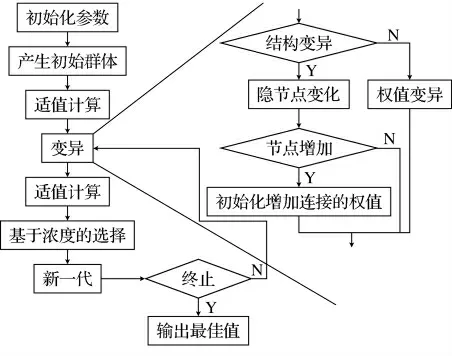
图3 进化神经网络的流程图Fig.3 Flow chart of evolutionary neural network

2 深部岩巷围岩力学参数反演研究

为了对深部岩巷围岩稳定性进行分析研究，首先必须对各种类型围岩体的物理力学性质进行研究.这里以淮南矿区两个典型矿井谢一矿和谢桥矿的试验巷道［5］为例，基于现场位移观测结果对围岩的物理力学参数进行反演分析研究.由于反分析计算需要比较完善的现场监测位移资料，为了使本次反分析研究的结果更具有代表性，考虑现场的监测结果，本次研究选取收敛位移断面进行参数反分析，采用多点位移计监测结果进行验证.

2.1 Ⅲ类围岩典型巷道围岩参数反分析

谢一矿-780mCS13底板运输巷的围岩稳定性在淮南矿区深部岩巷中具有代表性，属于中等偏差类型，应确定为Ⅲ类围岩.该巷道距地面800m 左右，岩性主要为中细砂岩、灰岩，其完整性较好.

巷道断面的位移监测布置见图4所示，其中，收敛监测点布置为左右帮的多点空外端，上下为上多点孔外端和底板正中心.

图4 监测断面布置示意图Fig.4 Layout of monitoring sections

其收敛监测数据如表1所示.通过多点位移计监测得到的深部位移结果如图5所示.

表1 谢一矿－780m底板运输巷收敛位移监测结果Table 1 Monitoring convergence displacements of－780mfloor roadway in Xieyi coal mine

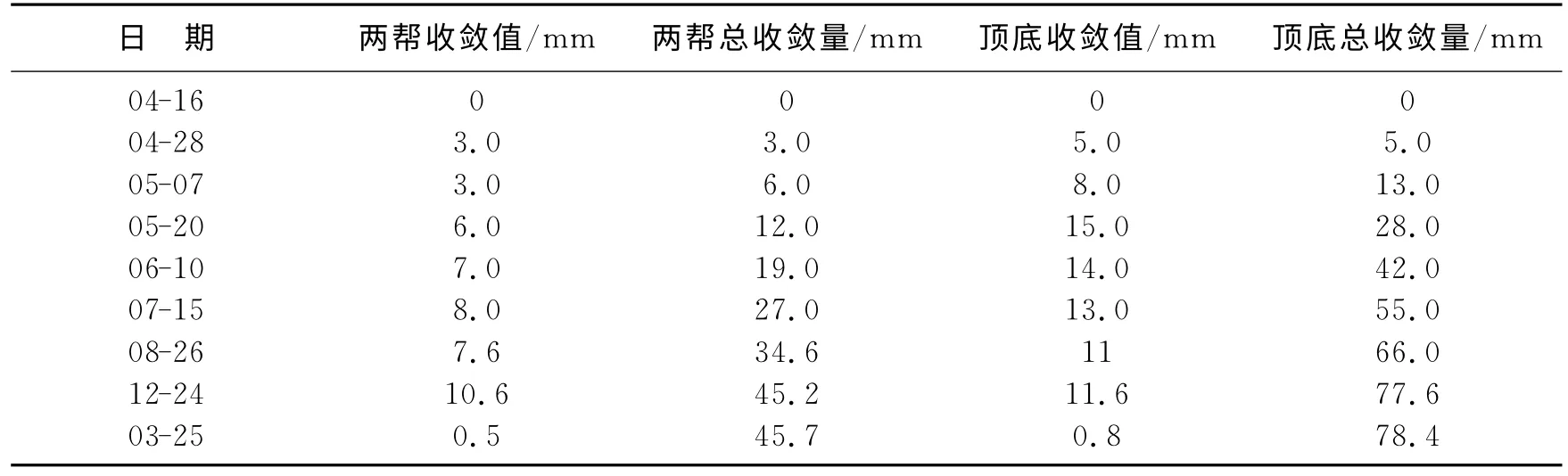
表1 谢一矿－780m底板运输巷收敛位移监测结果Table 1 Monitoring convergence displacements of－780mfloor roadway in Xieyi coal mine

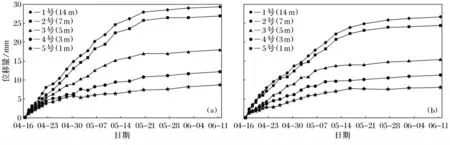
图5 谢一矿－780m底板运输巷深部位移监测结果Fig.5 Deep displacements of－780mfloor roadway in Xieyi coal mine

计算中取地应力值为现场实测值，具体数值为水平应力19.5MPa，垂直应力13.2MPa.有限元计算模型见图6.

模型边界条件为，上下为竖向约束，两侧为水平向约束.考虑到巷道断面尺寸为高2m，宽2.5 m的实际情况，模型计算区域为，巷道上下影响范围各为20m，左右影响范围各30m.

图6 围岩参数反分析计算模型Fig.6 Computation model of parameters back analysis

根据位移反分析计算的要求，先确定出各反演参数的计算范围，根据实测结果及工程经验，4个参数的计算搜索范围如下：

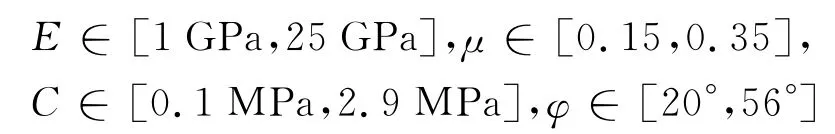
要进行反分析，首先应进行网络训练样本集的组织.这里以测线位移水平收敛及顶底板收敛作为输入，以物性参数弹性模量E、泊松比μ、内聚力C、内摩擦角φ 作为输出组成进化神经网络的训练样本集.

按照前面的分析，进化神经网络的样本集采用正交试验设计的方法进行组织.为此，首先将4个物性参数的试验水平设计为表2所示.

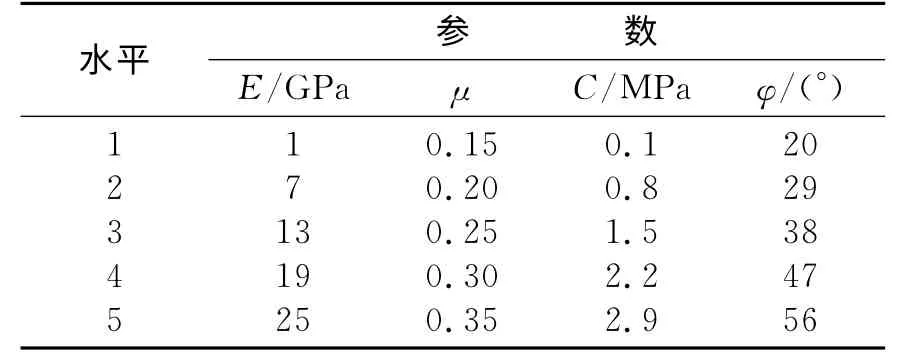
表2 反演参数的试验设计水平Table 2 The level of experimental design for parameters back analysis

根据试验因素及水平的数目，这里采用L25（56）正交表进行有限元正分析计算的参数组合，表3给出以此设计的有限元正分析计算的参数组合.

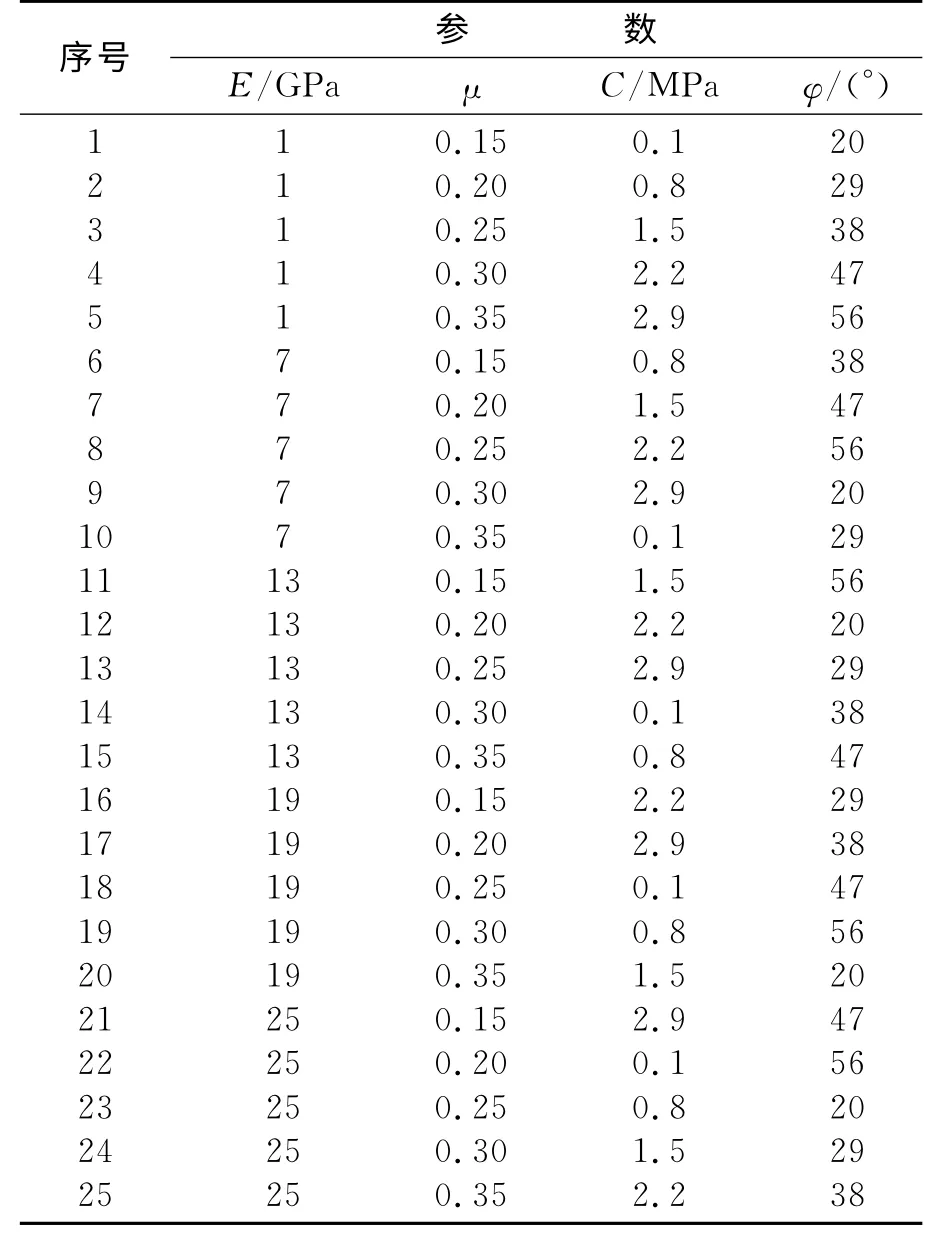
表3 有限元正分析计算参数组合表Table 3 Parameter combinations for FEM computation

按照表3所列各参数的组合进行有限元正分析计算得到2 个测线的模拟计算位移值如表4所示.

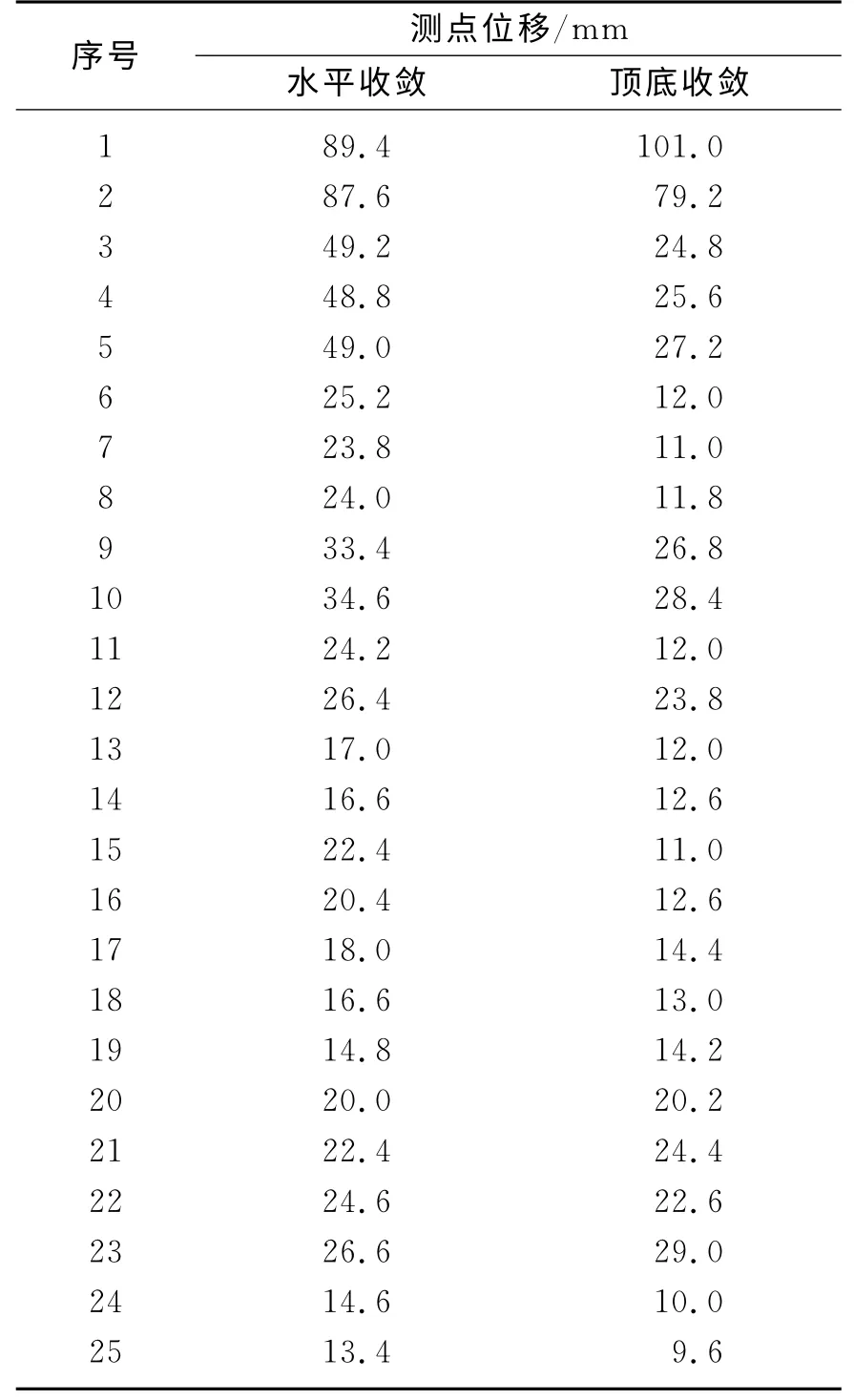
表4 测点的模拟计算位移结果Table 4 Computing displacements of measuring points

以表4所列水平收敛和顶底板收敛作为进化神经网络的输入，以其对应的参数组合（E、μ、C、φ）作为网络输出组成网络的训练样本对进化神经网络进行训练.进化训练中，各算法的参数取值依次为，神经网络的输入节点数为2，输出节点数为4，隐层节点的取值范围为（1～30），连接权值的初始取值为（-1.0～1.0）.进化算法的群体规模为150，进化代数阈值为200，同时限定最佳个体的最优误差为10-5.

把表3、表4中的25组位移-物性参数样本代入进化神经网络算法进行训练，最终在误差0.007 1的情况下，得到结构为2-4-4的神经网络能很好地实现上述样本所代表的映射，并具有良好的泛化预测能力.采用该网络进行围岩参数反分析计算，把收敛监测位移45.7和78.4作为网络两个输入量输入网络进行计算，可以得到4个输出结果，即对应于收敛监测位移的4个围岩参数，其结果整理如表5所示.

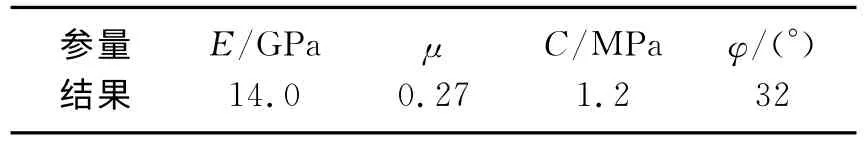
表5 围岩参数反分析结果Table 5 Back analysis results of surrounding rock parameters

为了验证反分析的计算结果，把表5中参量代入有限元模型进行计算，并与多点位移计的量测结果进行比较，其结果如表6和表7所示.

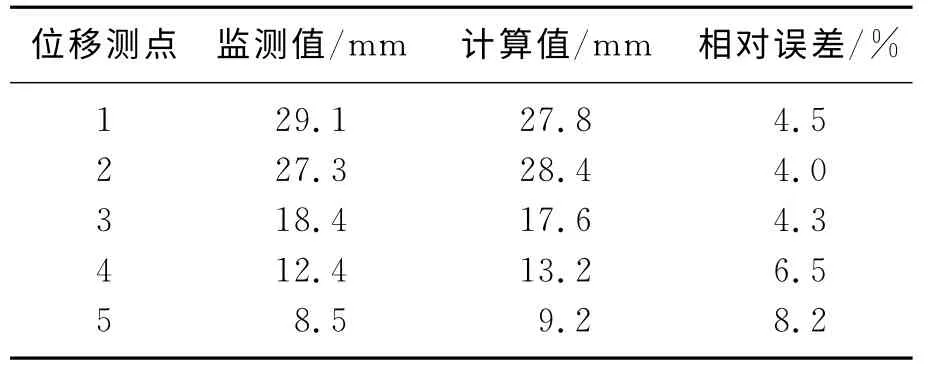
表6 帮部位移监测与计算结果对比Table 6 Comparision of computing displacements and measuring displacements on side

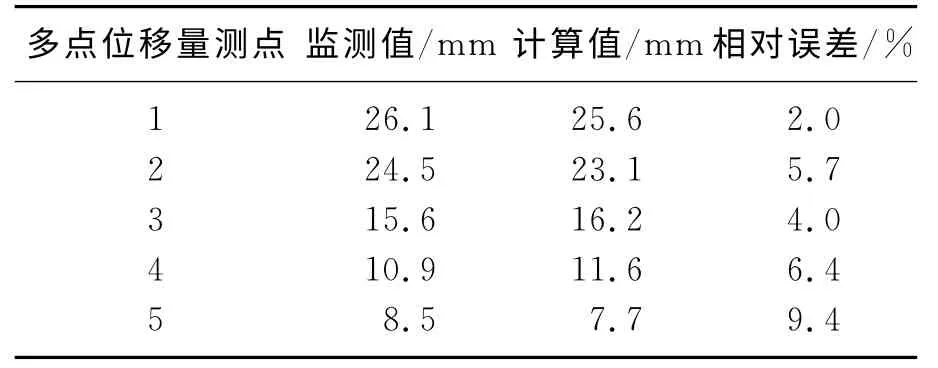
表7 顶部位移监测与计算结果对比Table 7 Comparision of computing displacements and measuring displacements on top

由表7可见，计算结果和监测结果的误差在10%以内，说明本次计算的反分析结果良好，基本得到了反映巷道围岩特性的物性参数.

2.2 Ⅱ类围岩典型巷道围岩参数反分析

谢桥矿-720m 水平轨道石门的围岩稳定性在淮南矿区深部岩巷中也具有代表性，该巷道围岩岩性以粉砂岩、粉细砂岩、中细砂岩为主，有薄层泥岩、砂质泥岩等组成，其完整性较好.属于中等偏好类型，应确定为Ⅱ类围岩.其监测断面布置同前节2.1.

其收敛监测数据如表8所示.通过多点位移计监测得到的深部位移结果如图7所示.

计算中取地应力值根据类似矿井现场实测值确定，具体数值为水平应力15.6MPa，垂直应力20.1MPa.有限元计算模型见图8.

模型边界条件为，上下为竖向约束，两侧为水平向约束.考虑到巷道断面尺寸为高1.5m，宽2 m的实际情况，并考虑上赋岩层地质条件，有限元计算区域为，巷道上影响范围为8m，下影响范围为15m，左右影响范围为各为20m.

同样根据实测结果及工程经验，先给出4个计算参数的计算搜索范围如下：

E ∈［1GPa，25GPa］，μ ∈［0.15，0.35］，C ∈［0.1MPa，2.9MPa］，φ ∈［20°，56°］

同理，首先将4个物性参数的试验水平设计为表9所示.

表8 谢桥矿－720m 水平轨道石门巷道收敛监测数据Table 8 Monitoring convergence displacements of－720mcross-cut roadway in Xieqiao coal mine

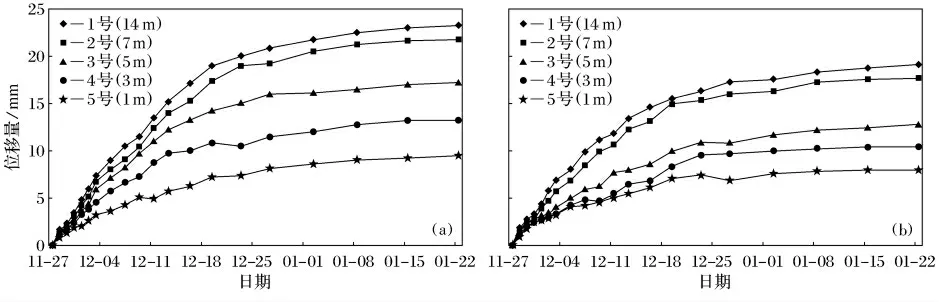
图7 谢桥矿－720m 水平轨道石门深部位移监测结果Fig.7 Deep displacements of－720mcross-cut roadway in Xieqiao coal mine

表9 反演参数的试验设计水平Table 9 The level of experimental design for parameters back analysis

根据试验因素及水平的数目，采用L25（56）正交表进行有限元正分析计算的参数组合（表10）.

表10 有限元正分析计算参数组合表Table 10 Parameter combinations for FEM computation

按照表10所列各参数的组合进行有限元正分析计算得到2 个测线的模拟计算位移值如表11所示.

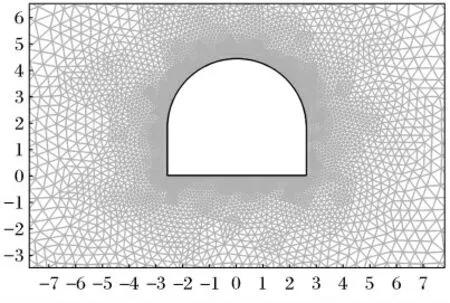
图8 反分析计算模型Fig.8 Computation model of parameters back analysis

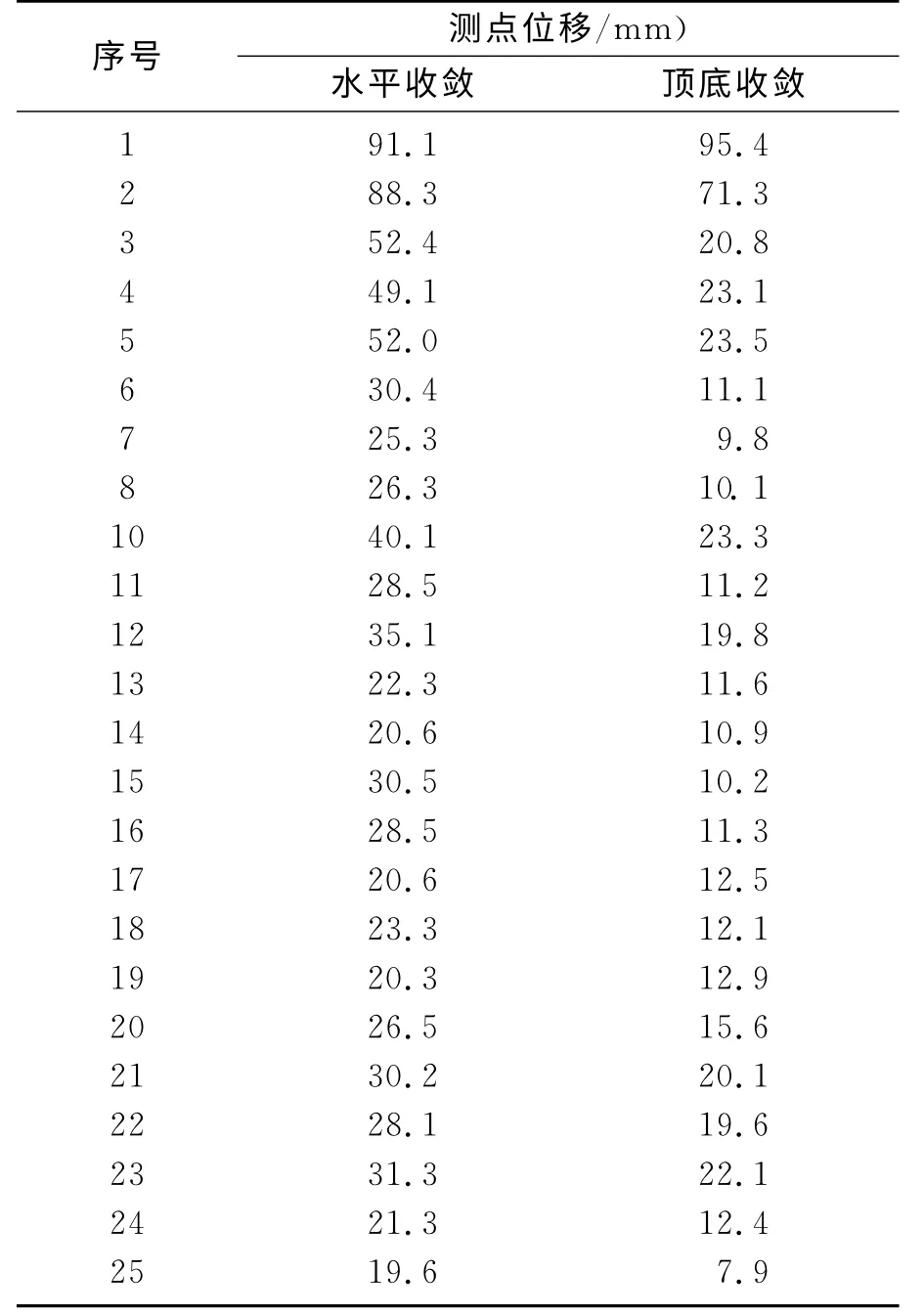
表11 测点的模拟计算位移结果Table 11 Computing displacements of measuring points

以表11所列水平收敛和顶底收敛作为进化神经网络的输入，以其对应的参数组合（E、μ、C、φ）作为网络输出组成网络的训练样本对进化神经网络进行训练.进化训练中，各算法的参数取值依次为，神经网络的输入节点数为2，输出节点数为4，隐层节点的取值范围为（1～30），连接权值的初始取值为（-1.0～1.0）.而进化算法的群体规模为150，进化代数阀值为200，同时限定最佳个体的最优误差为10-5.

把表10、表11中25组位移—物性参数样本代入进化神经网络算法进行训练，最终在误差为0.004 1的情况下，得到结构为2-7-4的神经网络能很好地实现上述样本所代表的映射，并具有良好的泛化预测能力.采用该网络进行围岩参数反分析计算，把收敛监测位移55.3和66.6作为网络两个输入量输入网络进行计算，最终得到4个输出结果，即对应于收敛监测位移的4个围岩参数，其结果整理如表12所示.

表12 围岩参数反分析结果Table 12 Back analysis results of surrounding rock parameters

为了验证反分析的计算结果，把表12参量代入有限元模型进行计算，并和多点位移计的量测结果进行比较，其结果如表13和表14所示.

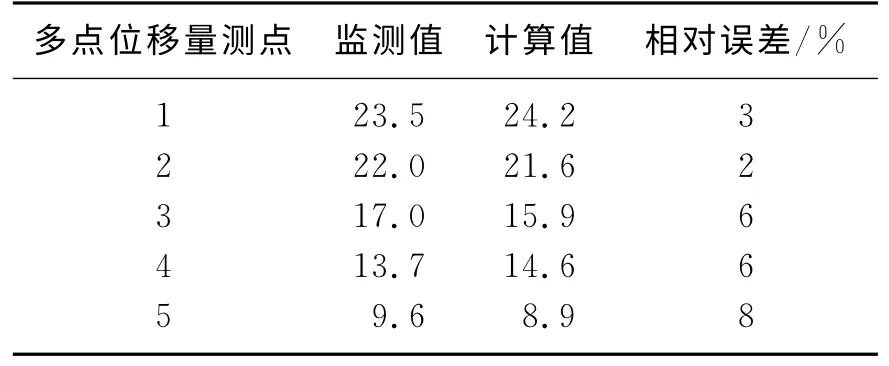
表13 帮部计算结果Table 13 Comparision of computing displacements and measuring displacements on side

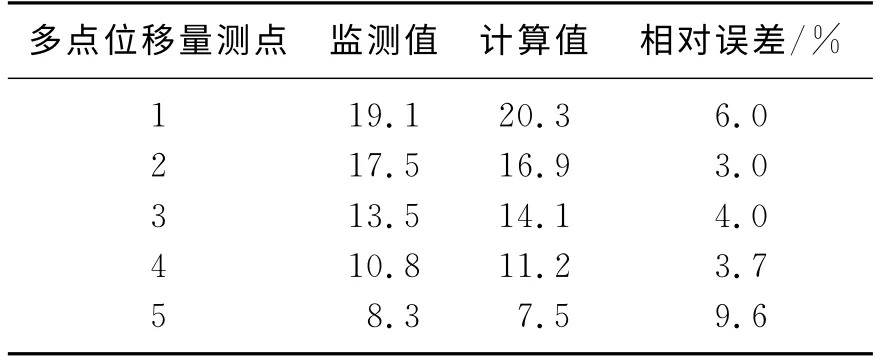
表14 顶部计算结果Table 14 Comparision of computing displacements and measuring displacements on top

由上表可见，计算结果和监测结果的误差在10%以内，说明反分析结果良好，基本得到了反映巷道围岩特性的物性参数.

3 结 语

随着资源开发的深入，淮南矿区已经整体进入了深部开采阶段.进入深部开采后，由于所处环境的不同，深部岩石巷道的变形破坏机理和浅部存在很大不同.为了进行巷道变形破坏机理的研究，采用实测位移反演确定围岩的物性参数意义重大.为此，基于淮南矿区两个典型巷道的位移实测结果，采用进化神经网络逆反分析法进行了典型岩类的参数反分析研究.而且，采用收敛位移反演得到的参数通过数值正分析计算得到的深部位移和实测误差在10%以内，证明本次反分析研究结果良好，基本得到了反映巷道围岩特性的物性参数.

［1］虎维岳，何满潮.深部煤炭资源及开发地质条件［M］.北京：煤炭工业出版社，2008：201-210.（Hu Weiyue，He Manchao.Geological Conditions for Deep Coal Mine Development［M］.Beijing：China Coal Industry Publishing House，2008：201-210.）

［2］何满潮，谢和平，彭苏萍，等.深部开采岩体力学研究［J］.岩石力学与工程学报，2005，24（16）：2803-2813.（He Manchao，Xie Heping，Peng Suping，et al.Study on Rock Mechanics in Deep Mining Engineering［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（16）：2803-2813.）

［3］贺永年，韩立军，邵鹏，等.深部巷道稳定的若干岩石力学问题［J］.中国矿业大学学报，2006，35（3）：288-295.（He Yongnian，Han Lijun，Shao Peng，et al.Some Problems of Rock Mechanics for Roadways Stability in Depth［J］.Journal of China University of Mining ＆Technology，2006，35（3）：288-295.）

［4］高玮，刘泉声.基于仿生计算智能的地下工程反分析理论与应用［M］.北京：科学出版社，2009：54-73.（Gao Wei，Liu Quansheng.Back Analysis of Underground Engineering based on Bionics Computation Intelligence Theory and Application［M］.Beijing：Scince Press，2009：54-73.）

［5］刘泉声，高玮，袁亮.煤矿深部岩巷稳定控制理论与支护技术及应用［M］.北京：科学出版社，2010：216-227.（Liu Quansheng，Gao Wei，Yuan Liang.Control Theory and Support Application of Deep Rock Roadways in Coal Mine［M］.Beijing：Scince Press，2010：216-227.）