基于区域聚类蚁群算法建立电网拓扑研究

汪 峰， 廖家平

(湖北工业大学电气与电子工程学院， 湖北 武汉 430068)

1 区域聚类蚁群算法

蚁群算法是继禁忌搜索算法、模拟退火算法、遗传算法等智能优化算法迅速发展和应用之后提出的一种新型启发式算法．它具有典型的群体智能的特性,该算法的主要特点是正反馈、分布式计算、鲁棒性和并行性等[1]．

聚类蚁群算法是在原始蚁群算法基础上进行了改进，将蚁群算法思想与聚类思想进行了融合而得到的．聚类分析的基本思想是所研究的样品(网点)或指标(变量)之间存在不同程度的相似性(亲疏关系——以样品间距离衡量)[2]．于是可以根据一批样品的多个观测指标来找出一些能够度量样品或指标之间相似程度的统计量，以这些统计量作为划分类型的主要依据．把一些彼此之间相似程度较大的样品(或指标)聚合为一类，把另外一些相似程度较大的样品(或指标)又聚合为另一类，直到把所有随机节点样品(或指标)聚合完毕．本文将N个点按照不同类进行划分，然后在各个类之间以及类与类之间按照一定规则进行连接[3-4]．在本文中用聚类蚁群算法将随机分布的发电机、负载以及变压器等的节点位置进行不同类的划分，然后在每个类之间以及类与类之间按照最优路径选择进行连接，最终得到电网拓扑结构图．

2 电网拓扑结构构建方法

2.1 电力系统随机拓扑的建立

现实生活中的发电厂,负载以及变压器的位置在电网建立之前都是随机的,因此节点位置在本文是随机的．用泊松分布，将N个节点随机地分布在一定区域．然后用聚类的蚁群算法做出一个简单互联的模型,这意味着没有自循环和孤岛．为了生成一个稀疏的网络要求N≫k≫ln(N)[5-6]．其中N代表节点的数量,k代表节点的平均度量．生成随机的拓扑,运用MATLAB编写程序来实现．这个过程主要分7个步骤来完成．介绍步骤之前,必须提出一些变量:C代表N个节点的坐标,是N×2矩阵．M代表蚂蚁的数量(其中M≥N)．这七个步骤分别为s1-s7∶ (s1)变量的初始化．在本部分中,先要指出问题的性质,用函数来计算节点之间的距离和一些变量,如:启发式因子,信息素矩阵,存储并记录该路径的生成、迭代次数,每一代的最佳路径,它的长度,每一代的平均路径长度．

D(i,j)=

(1)

式(1)中D(i,j)表示节点(i,j)之间的距离．(s2)把M只蚂蚁放到随机的N个节点上，具体操作就是首先把N个节点随机分布，然后把坐标定出来并把蚂蚁放到每个节点上．(s3)M只蚂蚁按照概率函数选择下一个节点，并各自完成自己的周游[7]．概率函数如

(2)

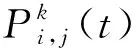
τi,j(t+1)=ρ*τi,j(t)+Δτi,j(t,t+1).

(3)

(4)

图1a中展示了电网拓扑模型的基本信息．图中各个节点所连的是多个闭合回路，从图1b可以看出，函数最后收敛到一条直线，而且从图1b可以发现：迭代次数在0～50之间时，函数的变化率很大，这表明了该算法的优越性；而随迭代次数的增加，函数变化率逐渐减小，说明了该算法的精确性及收敛性；迭代次数不到200时，函数值达到一条直线．由以上分析可以得出：这是多个闭合回路之间的互连，而且结果是收敛的．在节点较多、精度要求较高时，本文提出的方法较前文提到的方法迭代次数低，仿真时间短，操作简便．

(a)电网拓朴图

(b)收敛结果图 1 MATLAB仿真软件得到的电网拓扑结构图

2.2 电网参数的设置

为了形成对比以及方便进行电网动态特性分析，本文仿照参考文献[5]进行了参数设置．由于电力设备的不同，各个电力设备的各项参数也是不同的，这里随机的设置发电机、电机母线、节点间导线的阻抗、负载阻抗的参数．

发电机母线是从M条母线中随机选择的，但是第一条选择松弛母线并且被分配一个足够大的惯量．惯量M定义它的选择范围在[Mmin,Mmax]，瞬时阻抗jXd在范围[Xdmin,Xdmax]里面选择．发电机内电动势E是随机的在[Emin,Emax]里面选择．发电机内转角δ被设置为高斯随机变量，它由一个平均值和一个误差组成．即，在电力系统动态仿真中，可以改变转角来得到不同的状态．转角可以在[00,900]的范围里面变化，它可以体现不同条件下的扰动，因而在仿真外界不同扰动时可以改变转角的大小．

任意两个节点之间的阻抗正比于它们之间的物理长度，表示为

Zi,j=Z0Lm+σz.

(5)

式(5)中Zi,j表示任意两个节点之间的导线阻抗，Z0表示单位长度导线的阻抗，Lm表示任意两个节点之间导线的长度，σz表示随机偏差，它可以在范围[-σz,+σz]里面选择．

负载Rl+jXl可以用到所有总线上，Rl和jXl可以随机地设置(因为总线材料不同、制作不同等)．因此，本文建立的电网拓扑模型可以用来分析电网的动态特性．

3 电网拓扑构建特性分析

电网拓扑特性指标主要包括：电网的规模大小(包括任意两个节点之间的链接M，结点个数N),如公式(6)所示，k节点度量表示为

(6)

如公式(7)所示，l表示平均路径长度，它随着节点个数N的增加而增加[9]，lij表示任意两个节点之间的最短距离．

(7)

(8)

(9)

公式(10)所示，Dij表示任意两个节点之间的距离．

Dij=

(10)

公式(11)所示，ρ表示皮尔森相关系数度量．ρ是一个值，在一些网络下是正的，而在另外一些网络中是负的[10]．因此，在区分两个不同电力网络拓扑结构时它是有意义的．

(11)

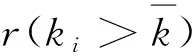
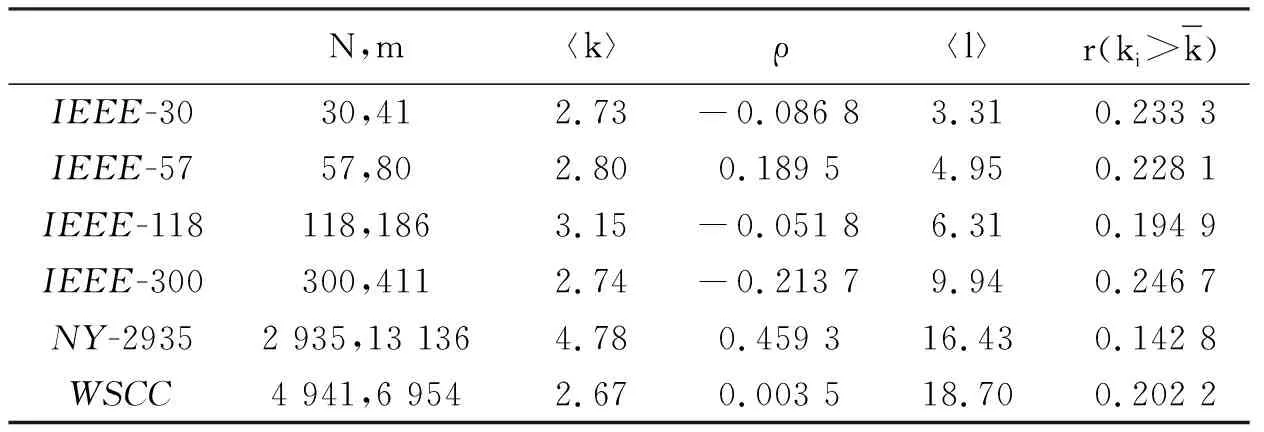
表1 已有电网拓扑特性

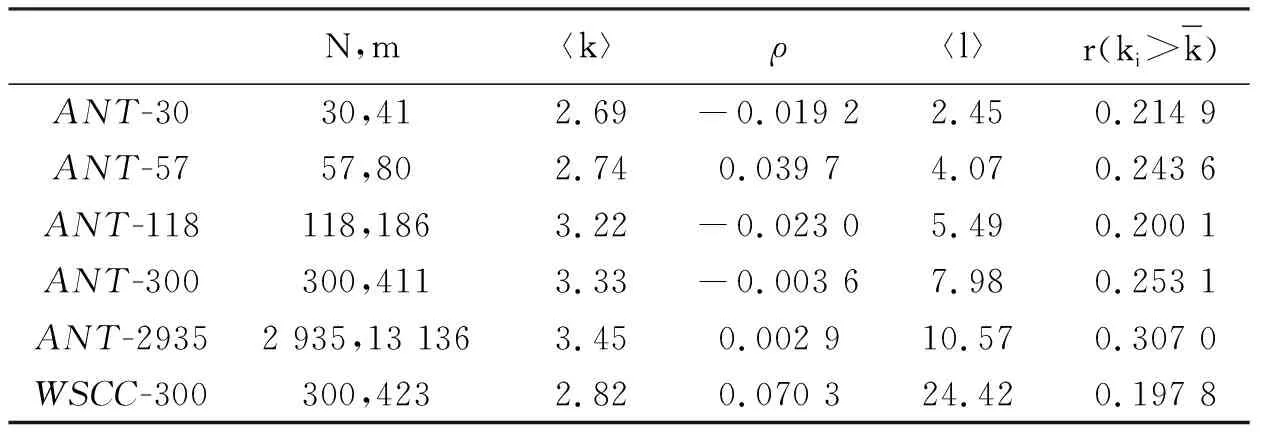
表2 本文电网拓扑特性

通过上面两个表的数据分析表明：利用蚁群算法得到的电网拓扑模型参数与IEEE系统基本相同，表明该算法可以进行电网拓扑结构的模拟．因此，这是一个较好的电网拓扑构建方法．本文利用MATLAB仿真软件内部M文件S函数来编程，将所需参数都在程序里面体现，这样通过改变程序里面的参数就可以模拟外界的各种扰动，例如改变M、Rl+jXl、δ等，这样弥补了原有方法只能在特定条件下模拟电网特性的不足，例如参考文献[11-13]中提到的情形．

4 电力系统特性

电网动态特性是非线性的，等效的线性化系统方程可以用来分析线性时变系统在每一个时间点的状态，这里借助电网动态方程来分析系统的稳定性．本文中，选择统计特征值的分布来分析所建立系统的动态特性．如公式(12)(13)所示，在不考虑阻尼效应，以及同步电机的惯性的条件下，可以表示为

,2,…，ng.

(12)

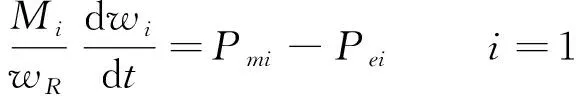
(13)

如公式(14)所示，电机i的功率输出可以表示为

δij+Gijcosδij).

(14)

其中δij=δi-δj，Ei是个定值，是电机i的内电动势，Yii=Gii+jBii，以及Yij=Gij+jBij分别是简化网络导纳矩阵的对角元素和非对角元素．经线性化的Pei给它设置一个变量δ0，δ0=[δ10δ20，…，δng0]T，这样得到系统的线性微分方程

δij0-Gijsinδij0)δijΔ=0

i=1,2,…，ng.

(15)

δiΔ是电机i相角δi0的增量，从公式(15)可以推出特征矩阵，相应的特征值可以根据δ0来计算得到．为了考虑不同的扰动，这里设置δ0高斯随机变量(mδ，δδ)．文中第二部分提出的mδ，δ0的变化可以代表系统不同相角变化．公式(15)表示系统在不同条件下的特征值，通过统计这些特征值的分布来分析系统的稳定性．

本文利用MATLAB仿真，首先给出IEEE系统在大量不同扰动条件下的特征值分布情况，然后给出本文提出的随机拓扑模型在相同扰动条件下的特征值分布情况．在图2a中给出特征值的分布情况．在b图中给出它的分布直方图．其中，图2a中X轴是实部，Y轴是虚部．

图 2 IEEE-30系统特征值分布图

图 3 IEEE-118系统特征值分布图

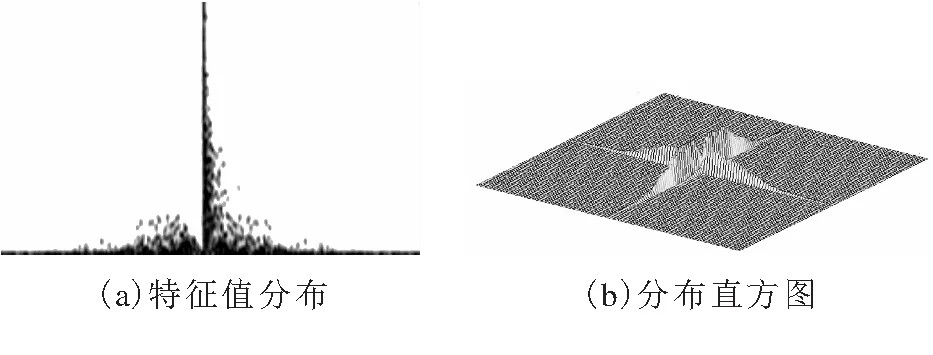
图 4 IEEE-300系统特征值分布图

本文提出的电网随机拓扑模型系统的特征值分布如图5-7．

图 5 泊松分布-30系统特征值分布图

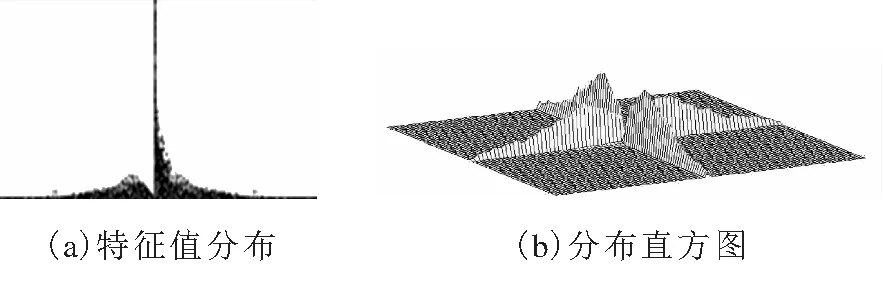
图 6 泊松分布-118系统特征值分布图

图 7 泊松分布-300系统特征值分布图

在30个节点的条件下，图5a图较图2a图中母线系统在右半平面的特征值分布较少，b图中在右边平面的直方图分布也可以明显看出．以此类推：图3与图6，图4与图7分布是节点在118个与300个的条件下得到的两种不同方法条件下的特征值分布图与节点概率分布图．通过比较图形2-4与图形5-7可以了解到.而本文提出的系统拓扑模型能反映与IEEE几乎相同的特征值分布，这说明了本系统的可行性．同时，通过比较两种系统的仿真图像可以发现，本文提出的母线系统特征值在右边平面的分布百分比进一步得到减小，也就是系统的稳定性得到了提升，仿真表明了该方法的优越性．同时在机器人项目中得到了充分应用，即在机器人发现足球到将球送入球门这个过程中得到了很好的体现．

5 结语

电网的稳定和安全运行是当前研究的一个重要课题．通过前文的分析得出：本文提出的模型基于区域聚类蚁群算法效果优于IEEE标准体系，该方法可以随机改变节点个数，即系统规模可以随机扩大；在此基础上,可以建立一个混合模型,即发电设备、电力设备、控制设备通过蚁群算法有序地连接起来；同时通过改变各项参数可以实现电力系统的动态特性分析，实时监测电网的运行，仿真结果表明本文提出的研究方法是可行的．它在机器人踢足球项目中得到了充分的应用，预测还可以被应用到交通系统最优路径寻优,城市输气管道的排布，以及各种优化统计工作．

[参考文献]

[1] 刘 杰，随星光.模糊聚类算法在Web使用挖掘中的应用[D].微型机与应用.2005，24(10):59-62.

[2] 陈冰梅, 樊晓平, 周志明,等.求解旅行商问题的Matlab蚁群仿真研究[J].电网技术2011，25(04)，256-280.

[3] 王会颖, 贾瑞玉, 刘慧婷, 等．一种求解TSP问题的分段交换蚁群算法[J].电网技术,2006，25(35)，34-36.

[4] Ziniu Wang, Song Li, Yan Wang et al． The research of Task Assignment Based on Ant colony Algorithm [J]. IEEE International Conference on Mechatronics and Automation, 2009(08):9-12.

[5] Zhifang Wang , Rpbert J. Thomas, Anna Scaglione :Generating Random Topology Power Grids Proceedings of the 41st Hawaii International Conference on System Sciences,2008：1-2.

[6] 贺 琦.基于GIS系统平台的电网拓扑生成研究[D].四川:四川大学图书馆，2004.

[7] Yan chen,Chun Minghong. Ant colony algorithm based on the optimal path selection[J]. 2007:1-2.

[8] Newman M. The Structure and Function of Complex Networks[J]. SIAM Review, 2003:1-2.

[9] Albert R, Barabasi A.Statistical mechanics of complex networks [EB/OL] .http://prola.aps.org/pdf/RMP/v74/i1/p47_1.

[10] Whitney D E, Alderson D. Are technological and social networks really different[J]. work to be published, 2003:1-2.

[11] 盛义发, 洪镇南.MATLAB在电力系统仿真中的应用[J].电网技术，2004, 30(11)，197-199.

[12] 都伟杰, 张俊芳, 刘 鹏,等.基于MATLAB的电力系统暂态稳定性仿真研究[J]. 电网技术，2009， 26(01):23-26.

[13] 何宏涛.电力系统动态特性分析的一种新方法[J].电网技术，2010，17(02):8-166.