基于粒子群优化核独立分量的特征降维算法及其应用研究
2013-11-12贾云献王卫国张英波赵劲松
孙 磊,贾云献,王卫国,张英波,赵劲松,3
(1.军械工程学院装备指挥与管理系, 河北石家庄 050003; 2.军械工程学院科研部, 河北石家庄 050003;3.军事交通学院装备保障系, 天津 300161)
为了更好地掌握装备的运行状态,在对装备实施状态监测时往往采集多种状态信息[1]。例如:对于油液光谱分析采集的元素种类多达20几种,这些状态信息间存在一定的相关性,若把这些状态信息直接用于装备的剩余寿命预测将导致计算量急剧增大或难以计算,而且由于引入了与装备状态相关度较小的状态信息而导致结果存在偏差。因此,如何从大量状态信息中提取影响装备寿命的主要特征信息,使得这些特征信息间既充分反映原来的状态信息的作用又彼此相互无关,就显得十分重要,为下一步的故障诊断与预测提供有效特征值[2-3]。
独立分量分析(independent component analysis,ICA)是近年来在信号分析与处理中发展形成的一种数据处理方法[4]。ICA作为一种有效的盲源分离技术仍是信号处理领域的热点,但目前的算法在处理非线性变化的信号时还有一定的局限,而基于非线性函数空间的ICA方法——核独立分量分析(kernel independent component analysis,KICA)[5]则可以解决这一问题。KICA方法具有更好的灵活性和鲁棒性,不仅能够实现高维非线性数据的降维,更重要的是,基于信号的高阶研究信号间的独立关系使经过变换所得到的各个分量之间不仅正交,而且相互独立,避免了数据的非线性对预测模型的影响[6-7]。
由于KICA算法精度受到核函数类型及其参数的影响,因此选择合适的核参数至关重要。目前核参数的选择方法仍是主要靠大量的试验人为确定或采用交叉检验的办法,不但费时费力效率低,而且这样确定的核函数参数不一定是最优的。因此,对KICA核函数参数的优化方法进行研究,对改善其特征降维结果具有重要的意义。粒子群优化算法(particle swarm optimization,PSO)是一种全局并行的寻优方法,近年来已在函数优化、自动控制、机器学习、人工生命等领域都得到了广泛的应用[8-9]。笔者针对KICA技术在核函数参数选择上的盲目性,首先利用Fisher判别函数的思想建立核函数的参数优化的适应度,进而基于PSO算法求出核函数参数优化模型的全局最优解,改善KICA的性能。最后通过案例验证了方法的可行性与有效性。
1 独立分量分析
假设S=[s1,s2,…,sn]T为n个相互独立的源信号,X=[x1,x2,…,xn]T为m个观测信号,其满足以下关系[10]:
X=AS。
式中:A为m×n阶矩阵,该式表示了观察所得的状态变量是如何由独立分量构成的。目的是通过观测数据x估计未知独立源s和混合矩阵A,即求解一个解混矩阵W,使得
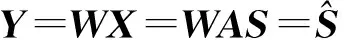
的各分量相互独立,并把Y作为S的估计。独立分量分析中所有的出发点都是一个基本假定:即认为这些独立分量si互相统计独立,且不服从高斯分布。若记Y=WTX,则可以通过最大化WTX的非高斯性来求W,从而求得独立分量Y。
2 核独立分量分析
2.1 Mercer核
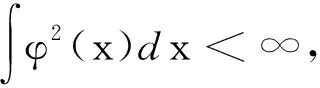
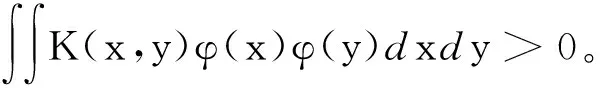
事实上任何一个函数只要满足Mercer条件,就可以用作Mercer核,同时可以分解成特征空间的点积形式。假设输入空间的样本xk∈RN,k=1,2,…,l,被某种非线性映射φ映射到某一特征空间R,得到φ(x1),φ(x2),…,φ(xl)。那么输入空间的内积运算,在特征空间就可以用Mercer核表示为K(xi,xj)=φ(xi)·φ(xj)。
2.2 KICA算法步骤
输入:数据矢量x1,x2,…,xn和核函数K(x,z)。
1)对输入数据矢量x1,x2,…,xn进行预白化处理,使输入的向量之间相互正交。
2)利用Cholesky分解求出原始独立数据z1,z2,…,zn的Gram矩阵K1,K2,…,Km,其中zi=Wxi,W为独立分量分析中的解混矩阵。
3)定义λH(K1,K2,…,Km)为下式的最大特征值:
(1)
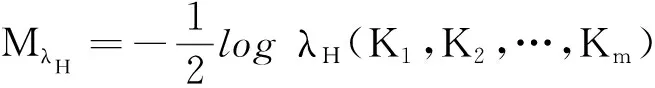
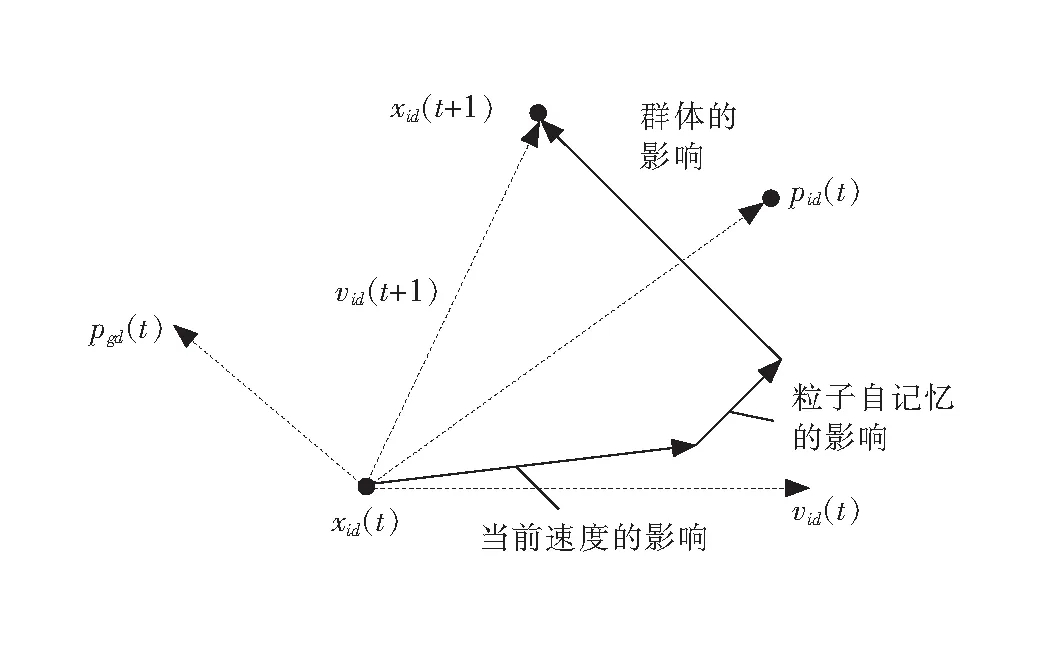
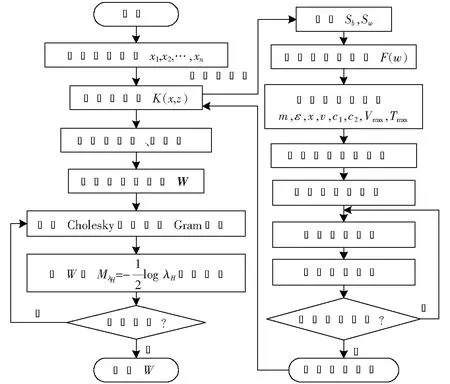
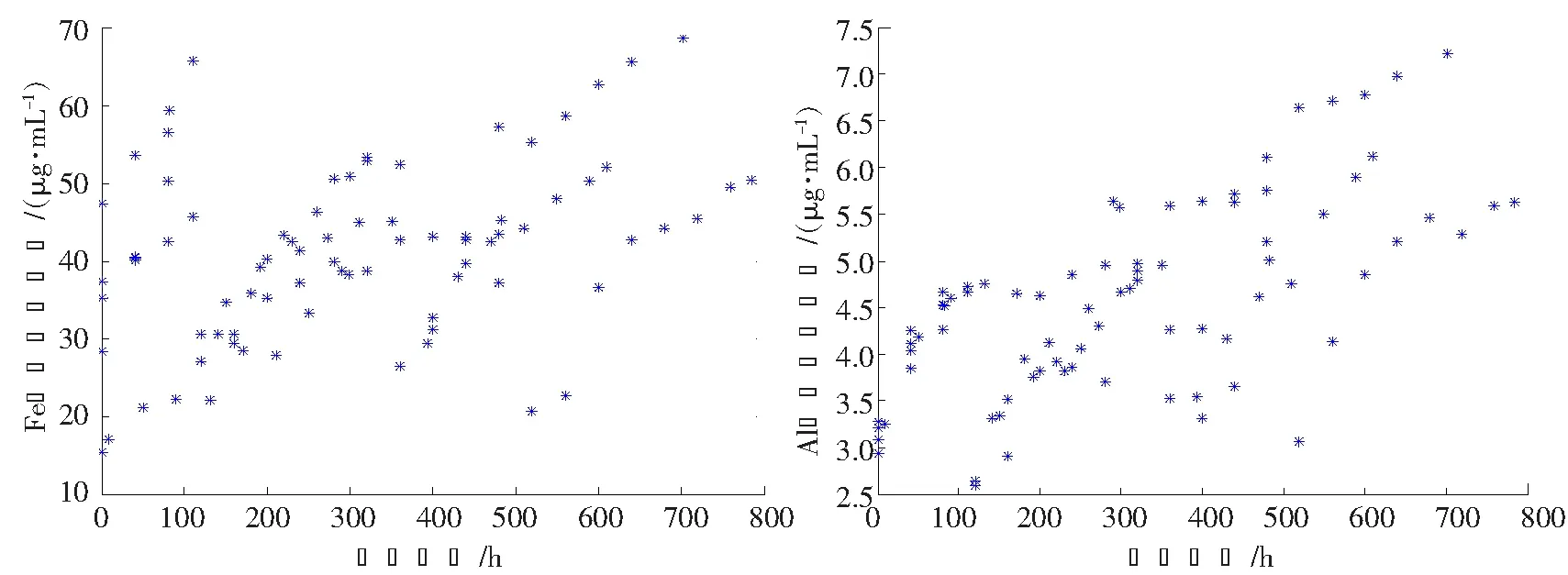
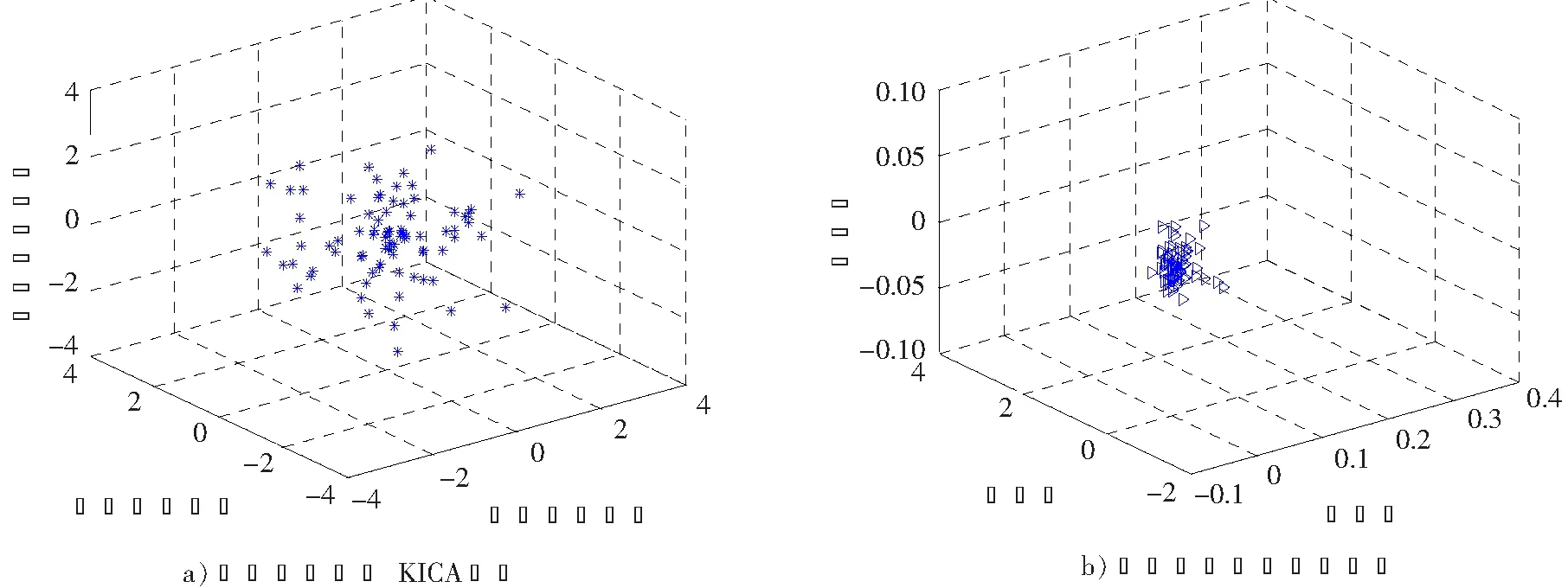
输出:W矩阵。上面的算法不断在步骤2)和4)之间重复运行,直到满足了收敛性的条件便可以得到解混矩阵W,W为m×n阶(m 图1 粒子位置更新示意图Fig.1 Scheme of particle position updating PSO算法将每个优化问题的潜在解看作是搜索空间的粒子,每个粒子都有一个被优化函数决定的适应值和一个决定其运动方向和距离的速度向量,然后粒子群就追随当前的最优粒子在解空间进行搜索[11]。PSO初始化为一群随机粒子,通过不断迭代搜索最优解。在每一次迭代中,粒子通过跟踪2个极值来更新自己,一个就是粒子本身到当前时刻为止找到的最优解,称为个体最优值;另一个就是整个种群到当前时刻找到的最优解,称为全局最优值,粒子位置更新过程如图1所示。 图中:xid(t)为第i个粒子的当前位置;vid(t)为第i个粒子的当前速度,vid∈[-Vmax,Vmax],Vmax是最大限制速度,非负;pid(t)为第i个粒子迄今为止搜索到的最优位置;pgd(t)为整个粒子群搜索到的最优位置。 假设在一个D维的目标搜索空间中,有m个粒子组成一个群体,其中第i个粒子的位置表示为向量xi=(xi1,xi2,…,xiD),i=1,2,…,m,其速度也是一个D维的向量,记为vi=(vi1,vi2,…,viD)。第i个粒子迄今为止搜索到的最优位置为pi=(pi1,pi2,…,piD),整个粒子群搜索到的最优位置为pg=(pg1,pg2,…,pgD),粒子更新公式如下[12]: vid(t+1)=vid(t)+c1r1(pid-xid(t))+c2r2(pgd-xid(t)); (2) xid(t+1)=xid(t)+vid(t+1)。 (3) 将式(2)称为基本粒子群优化算法。其中,当vid>Vmax时,取vid=Vmax;当vid<-Vmax时,取vid=-Vmax;i=1,2,…,m;d=1,2,…,D;加速常数c1和c2为非负常数;r1和r2服从[0,1]上的均匀分布随机数。 大量数值实验表明,核参数的取值对基于核函数的特征降维算法性能具有很大的影响。例如:高斯径向基核函数σ过大,样本“势力范围”也会过大,以致一些毫无关系的训练样本会干扰对新测试样本作出正确判断;σ过小,则会导致核学习只有记忆功能而无法对新样本进行判断[13]。所以选择合适的函数宽度需要在两者之间进行权衡。 根据前面的分析,KICA的主要思想是使得各分量的数据点散布于最大统计相关方向,强调的是分解出来的各分量之间的相互独立性。而Fisher线性判别分析(fisher linear discriminant analysis,FDA或LDA)的基本思想是选择使得Fisher准则函数达到极值的向量作为最优投影方向,把原始数据沿该方向进行投影得到一条直线,使投影后不同类别的数据尽可能分开,相同类别的数据则尽可能的聚集,即投影后模式样本的类间散布最大而类内散布最小。因此,基于KICA和FDA基本思想之间的相通性,可以借鉴FDA的思想来探索KICA中核参数优化方法。 1)建立核参数优化适应度函数 设X1,X2,…,XD是特征空间D个样本类,特征样本X为n维实向量,即X∈Rn,经过非线性映射Φ后对应样本向量为Φ(X)∈H。则样本类Xi在特征空间的均值向量为 (4) 式中,ni为第i个样本类的样本数。 定义样本的类间散度Sb为 (5) 定义样本的类内散度Sw为 (6) 式中,Φ(xij)表示特征空间H中第i类第j个样本。对于高斯径向基核函数,由于k(xij,xij)的值等于1,所以对高斯径向基函数式(6)可以简化为 (7) 那么,根据Fisher极小鉴别准则,在此建立适应度函数为 (8) 实验表明,对于完全非线性可分问题,Fisher鉴别函数F(w)的极小值点w*存在[14]。对于高斯径向基核函数把w*作为参数σ的值可以取得较好的效果;而对于多项式核函数则把w*作为多项式的阶次d的取值。对于线性可分或几乎线性可分问题,随着w由小变大,F(w)值急剧下降,然后趋于平稳,此时可以取F(w)开始趋于平稳时的w作为w*。 2)KICA算法中核参数的粒子群优化过程 在实现核参数优化过程中,对于适应度函数式(8),需要求Fisher鉴别函数F(w)的极值点。F(w)有可能是多峰值函数,存在多个极值点。为了得到全局最优值,在此结合PSO算法对参数w进行优化,建立PSO-KICA算法流程,如图2所示。具体步骤如下。 输入:数据样本x1,x2,…,xn,选择核函数K(x,z)。 图2 PSO-KICA算法流程Fig.2 Flow chart of PSO-KICA 1)计算样本的类间散度Sb和类内散度Sw; 2)构建Fisher鉴别函数F(w)作为粒子群优化的适应度函数; 3)给定核参数w的取值范围(wmin,wmax)、种群规模m、加速常数c1和c2、最大进化代数Tmax、最大限制速度Vmax、惯性权重ω和计算精度ε。 4)随机产生初始群体,计算个体适应度值Fp和种群整体适应度值Fg; 5)对粒子的位置和速度进行更新; 6)判断迭代次数t是否达到最大进化代数Tmax或评价值小于给定精度ε。如果达到最大进化代数Tmax或评价值小于给定精度ε,得到最优核参数w; 7)利用优化的核函数实现KICA算法。 输出:根据z=Wx分离出相互独立的信号。 由于自行火炮发动机工作条件复杂多变、工作环境相对恶劣,对其进行状态监测往往采用油液分析方法提取润滑油中金属元素的成分和浓度。然而,油液数据大多具有高维、非线性特点,不利于进一步的分析处理,人们往往采用降维的手段对其进行分析处理。 为验证上述所建立的基于粒子群优化算法的核独立分量分析技术的可行性和有效性,采用油液光谱分析的监测方式采集某型发动机润滑油中各元素的浓度为状态信息[15]。笔者重点收集了该发动机润滑油中铁、铝、铅、硼、钡、铬、镁、硅等8种元素浓度值。图3是原始的油液光谱分析数据散点图(由于篇幅所限仅给出Fe元素和Al元素的浓度散点图)。 图3 Fe元素和Al元素浓度散点图Fig.3 Graphical of iron and aluminum oil concentration records 基于油液浓度数据,采用PSO算法对KICA中的高斯径向基核函数参数进行优化,确定KICA分析的最优核函数,参数收敛过程如图4所示。可见,当核函数参数进化到50代时,适应度函数已收敛到规定的精度要求并逐渐趋于稳定,且核函数宽度也逐渐收敛于1。即当高斯径向基核函数σ=1.07时,适应度函数F(w)取得最优值为3.428 6。 图4 基于PSO的高斯径向基核函数参数优化Fig.4 Parameter optimizion of gausion kernel function based on PSO 图5 油液浓度数据特征降维结果Fig.5 Feature dimension reducing result of oil concentration data 图6 原始油液梯度数据投影和梯度数据KICA投影Fig.6 Projective and KICA projective chart of oil concentration data 得到最优核函数之后,根据前述降维算法对发动机油液浓度数据进行降维分析与处理,得到了3个独立主成分,如图5所示。图6a)是油液浓度数据进行PSO-KICA算法降维后,前3个独立成分在空间的投影图,可见各个分量之间具有较好的独立性。而未经KICA分析处理的原始数据则存在较大的相关性,如图6b)所示。利用PSO-KICA算法对油液浓度数据进行处理的过程表明,该算法不仅避免了核函数参数选择过程的盲目性,而且实现了高维非线性数据的降维,得到了相互独立的特征分量。 针对KICA特征降维算法在核函数参数的选择上存在的问题,利用PSO算法实现了核函数参数的优化,建立了基于PSO-KICA的特征降维算法。通过对某自行火炮发动机油液浓度数据进行降维处理,达到了基于PSO-KICA降低特征向量的维数的目的,验证了该方法用于特征降维的可行性和有效性。 参考文献/References: [1] JARDINE A K S,LIN D,BANJEVIC D. A review on machinery diagnostics and prognostics implanting condition-based maintenance[J]. Mechanical System and Signal Processing, 2006, 20(1): 1 483-1 510. [2] ABRAHAM B,MEROLA G. Dimensionality reduction approach to multivariate prediction[J]. Computational Statistics and Data Analysis, 2005, 48(1):5 016. [3] 欧阳晓黎,张延生,杨 军. 复杂电子装备智能故障诊断方法[J]. 河北科技大学学报, 2004,25(2):42-49. OUYANG Xiaoli,ZHANG Yansheng,YANG Jun. The intelligent fault diagnosis methods for complex electronic equipments[J]. Journal of Hebei University of Science and Technology, 2004, 25(2):42-49. [4] COMON P. Independent component analysis-a new concept[J]. Signal Processing, 1994(36):287-314. [5] 胥永刚, 李 强, 王正英, 等. 基于独立分量分析的机械故障信息提取[J]. 天津大学学报, 2006, 39(9) :1 066-1 071. 一篇好的文章,里面的语法必须要使用规范。学生在英语写作当中必须要注意语法的使用,如果出现了语法错误,那么整个句子就达不到所要表达的意思,当然,所有的章节也会失去本身的含义。 XU Yonggang, LI Qiang, WANG Zhengying, et al. Fault information extraction of mechanical equipment based on independent component analysis[J]. Journal of Tianjin University, 2006, 39(9):1 066-1 071. [6] FAUVEL M,CHANUSSOT J,BENEDIKTSSON J A. Kernel principal component analysis for feature reduction in hyperspectral images analysis[A]. Proceedings of the 7th Nordic[C].[S.l.]: Signal Processing Symposium, 2006.238-241. [7] XU Anbang, JIN Xin, GUO Ping. KICA feature extraction in application to FNN based image registration[A]. 2006 International Joint Conference on Neural Networks[C].[S.l.]:[s.n.], 2006.3 602-3 608. [8] 高 峰,武 睿,刘南平.基于自适应蚊群算法的无线传感器网络能量优化[J]. 河北工业大学学报, 2010,39(16):4-7. GAO Feng,WU Rui,LIU Nanping.An approachto WSN energy optimization based on self-adaptive ant colony algorithm[J]. Journal of Hebei University of Technology, 2010,39(6):4-7. [9] 李正涛,赵环宇,马献果. 应用粒子群算法从已知数据中确定置信测度和似然测度[J]. 河北科技大学学报,2011, 32(2): 128-132. [10] BACH F R, JORDAN M I. Kernel independent component analysis[J]. Machine Learning Research, 2002(3): 1-48. [11] 何学文. 基于支持向量机的故障智能诊断理论与方法研究[D]. 长沙:中南大学, 2004. HE Xuewen. Research on Fault Intelligent Theory Based on SVM [D]. Changsha: Central South University, 2004. [12] KENNEDY J,EBERHART R. Particle swarm optimization[A]. Proc IEEE Int'l Conf on Neural Networks, IV. Piscataway[C]. NJ: IEEE Servive Center, 1995. 1 942-1 948. [13] 魏秀业. 基于粒子群优化的齿轮箱智能故障诊断研究[D]. 太原:中北大学,2009. WEI Xiuye. Study on Intelligent Fault Diagnosis of Gearbox Based on Particle Swarm Optimization [D]. Taiyuan:North University of China, 2009. [14] 褚蕾蕾, 陈绥阳, 周 梦,等. 计算智能的数学基础[M]. 北京: 科学出版社, 2002. CHU Leilei, CHEN Suiyang, ZHOU Meng,et al. Mathematics Foundation of Computation Intelligent[M]. Beijing: Science Press, 2002. [15] 陈 丽. 基于状态的维修模型及应用研究[D]. 石家庄:军械工程学院,2009. CHEN Li. Condition Based Maintenance Model and Application[D]. Shijiazhuang :Ordance Engeerning College, 2009.3 基于粒子群优化算法的核独立分量分析技术
3.1 基本PSO算法
3.2 基于PSO的核函数参数优化方法
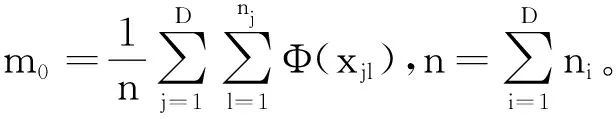
4 案例分析


5 结 语
