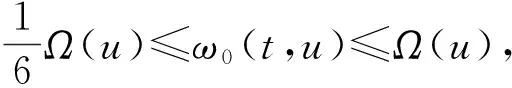具有变号非线性项的脉冲微分方程边值问题的正解
2013-11-12江卫华郭巍巍
江卫华, 张 强, 郭巍巍
(河北科技大学理学院,河北石家庄 050018)
脉冲微分方程在经济、生物、生态学等领域有着广泛的应用[1-3],考虑到其影响,很多学者常将微分方程边值问题推广到脉冲微分方程上去,通过运用锥拉伸与锥压缩不动点定理、Leray-Schauder不动点定理、不动点指数理论等方法,得到了脉冲微分方程边值问题解的存在性[4-21]。
在文献[4]中,AGARWAL等利用非线性的Leray-Schauder不动点定理和Krasnoselskii's不动点定理得到了二阶脉冲微分方程边值问题:
至少存在1个解和2个解的充分条件。
在文献[5]中,AGARWAL等又利用Legget-Williams不动点定理得出了脉冲微分方程边值问题
至少存在3个正解的充分条件。
在文献[6]中,李高山等运用锥拉伸与锥压缩不动点定理,得到了带有变号非线性项的二阶三点微分方程边值问题:
其中α,η∈(0,1),至少1个正解的充分条件。
对于具有变号非线性项一阶导带脉冲的微分方程边值问题还没有人研究,应用文献[28]中的方法,笔者考虑下面脉冲微分方程边值问题:
(1)
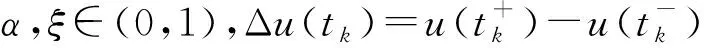
定义空间:PC[0,1]={u:[0,1]→R,u(0)=u(0+0),存在uj∈C[tj,tj+1],使得在(tj,tj+1]有u=uj,j=0,1,…m)}。范数为‖u‖=sup{|u(t)|:t∈[0,1]{t1,t2,…,tm}},其中t0=0,tm=1。
定义1u∈PC[0,1]是边值问题(1)的正解,当且仅当u>0且满足边值问题(1)。
在本文中,总是假设以下条件是成立的:
C1)f∈C([0,1]×R+,R),存在M>0,使得对于(t,u)∈[0,1]×R,有f(t,u)≥-M;
C2)Ik,Jk:R+→R是连续的,k=1,2,…,m;
C3)存在一个函数Ω:{u:u∈PC[0,1],u>0}→R+和一个正的常数c0∈(0,1)使得
c0Ω(u)≤ω0(t,u)≤Ω(u),
其中:
下面的定义及定理是本文的关键所在,具体见文献[28]。
定义2当且仅当φ:P→R+是连续的且对于所有的x,y∈P和t∈[0,1],有
φ(tx+(1-t)y)≥tφ(x)+(1-t)φ(y),
称映射φ是实Banach空间E中锥P上的一个非负、连续、凹函数。
定义3当且仅当Φ:P→R+是连续的且对于所有的x,y∈P和t∈[0,1],有
Φ(tx+(1-t)y)≤tΦ(x)+(1-t)Φ(y),
称映射Φ是实Banach空间E中锥P上的一个非负、连续、凸函数。
令φ和Θ是锥P上的非负、连续凸函数,Φ是锥P上的非负连续凹函数,Ψ是锥P上的非负连续函数,定义以下集合:
P(φ,d)={x∈P:φ(x) P(φ,Φ,b,d)={x∈P:b≤Φ(x),φ(x)≤d}, P(φ,Θ,Φ,b,c,d)={x∈P:b≤Φ(x),Θ(x)≤c,φ(x)≤d}, R(φ,Ψ,a,d)={x∈P:a≤Ψ(x),φ(x)≤d}, 其中a,b,c和d都是正数。 利用以下Avery-Peterson不动点定理来研究边值问题(1)。 S1)对于x∈P(φ,Θ,Φ,b,c,d),有{x∈P(φ,Θ,Φ,b,c,d):Φ(x)>b}≠φ和Φ(Tx)>b; S2)对于x∈P(φ,Φ,b,d)和Θ(Tx)>c,有Φ(Tx)>b; S3)对于x∈R(φ,Ψ,a,d)和Ψ(x)=a,有0∉R(φ,Ψ,a,d)和Ψ(Tx) 引理1u是边值问题(1)的解的充要条件是u满足积分方程 其中: k=1,2,…,m, (t,u)∈[0,1]×{u:u∈PC[0,1],u>0}且有c0Ω(u)≤ω01(t,u)≤Ω(u)。 引理2函数G(t,s)在[0,1]×[0,1]上是连续的且满足 ρ0g(s)≤G(t,s)≤g(s),t,s∈[0,1], 引理3微分方程边值问题: (2) (3) (4) 证明如果u是边值问题(1)的一个正解,由引理3可知u满足: (5) 显然当u≥My是算子T的一个不动点,那么u-My是边值问题(1)的一个正解。 引理5算子T:K→K是全连续的。 证明取u∈K,显然Tu∈PC[0,1]。 因为 故T:K→K。 故T(B)是有界的。 令t1,t2∈[0,1],t1 所以T(B)是等度连续。因此知算子T:K→K是全连续的。 则边值问题(1)至少存在2个正解。 下面证明条件S1)成立。 因此条件S1)满足。 以下证明条件S2)成立。 表明条件S2)满足。 接下来证明条件S3)成立。 显然,φ(0)=0 因此,条件S3)也满足。 由定理2知,算子T至少存在3个正解u1,u2,u3,满足:‖ui‖≤d,i=1,2,3,并且 如果u∈K且‖u‖≥a,由式(3)和定理2知u(t)≥ρ‖u‖≥ρa≥My(t)。显然,u2≥a,u1>b>a。所以可得到u1-My,u2-My是边值问题(1)的2个正解。 考虑下面边值问题: (6) 其中: 参考文献/References: [1] LAKSHMIKANTHAM V, BAINOV D D, SIMEONOV P S. Theory of Impulsive Differential Equations[M].Singapore: World Scientific, 1989. [2] SAMOILENKO A M, PERESTYUK N A. Impulsive Differential Equations[M]. River Edge: World Scientific, 1995. [3] BAINOV D D, SIMEONOV P S. Impulsive Differential Equations: Periodic Solutions and Applications[M]. Harlow: Longman Scientific and Technical, 1993. [4] AGARWAL R P, REGAN D O. Multiple nonnegative solutions for second order impulsive differential equations[J]. Appl Math Comput, 2000,114: 51-59. [5] AGARWAL R P, REGAN D O. A Multiplicity result for second order impulsive differential equations via the Leggett Williams fixed point theorem[J]. Appl Math Comput, 2005,161:433-439. [6] LI Gaoshang, LIU Xiping, JIA Mei. Positive solutions to a type of nonlinear three-point boundary value problem with sign changing nonlinearities[J]. Comput Math Appl, 2009,57:348-355. [7] GUO Dajun, LIU Xinzhi. Multiple positive solutions of boundary value problems for impulsive differential equations[J]. Nonlinear Anal, 1995,25: 327-337. [8] FRIGON M, REGAN D O. Boundary value problems for second order impulsive differential equations using set-valued maps[J]. Appl Anal, 1995,58:325-333. [9] ELIE P W, HENDERSON J. Positive solutions of boundary value problems for ordinary differential equations with impulsive[J]. Dynamics Contin Discrete Impulsive Syst, 1998,82(4): 285-294. [10] NIETO J J. Periodic boundary value problems for first-order impulsive ordinary differential equations[J]. Nonlinear Anal, 2002,51:1 223-1 232. [11] ZHAO Aimin, BAI Zhenguo. Existence of solutions to first-order impulsive periodic boundary value problems[J]. Nonlinear Anal, 2009,71:1 970-1 977. [12] LIANG Ruixi, SHEN Jianhua. Periodic boundary value problem for second-order impulsive functional differential equations[J]. Appl Math Comput, 2007, 193: 560-571. [13] LI Jianli, SHEN Jianhua. Periodic boundary value problems for impulsive integro-differential equations of mixed type[J]. Appl Math Comput, 2006, 183: 890-902. [14] HE Zhimin, YU Jianshe. Periodic boundary value problem for first-order impulsive functional differential equations[J]. J Comput Appl Math, 2002, 138(2):205-217. [15] JANKOWSKI T. Positive solutions to second order four-point boundary value problems for impulsive differential equations[J]. Appl Math Comput, 2008, 202:550-561. [16] JANKOWSKI T. Positive solutions of three-point boundary value problems for second order impulsive differential equations with advanced arguments[J]. Appl Math Comput, 2008, 197: 179-189. [17] ZHANG Xuemei, YANG Xiaozhong, GE Weigao. Positive solutions of th-order impulsive boundary value problems with integral boundary conditions in Banach spaces[J]. Nonlinear Anal, 2009, 71:5 930-5 945. [18] HAO Xinan, LIU Lishan, WU Yonghong. Positive solutions for second order impulsive differential equations with integral boundary conditions[J]. Commun Nonlinear Sci Numer Simul, 2011, 16(1): 101-111. [19] GUO Dajun. Multiple positive solutions of a boundary value problem fornth-order impulsive integro-differential equations in Banach spaces[J]. Nonlinear Anal, 2005, 63: 618-641. [20] HU Lili, LIU Lishan, WU Yonghong. Positive solutions of nonlinear singular two-point boundary value problems for second-order impulsive differential equations[J]. Appl Math Comput, 2008, 196: 550-562. [21] JANKOWSKI T.Positive solutions for second order impulsive differential equations involving stieltjes integral conditions[J]. Nonlinear Anal,2011,74:3 775-3 785.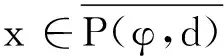
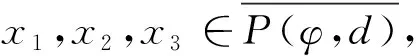
1 预备知识

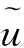
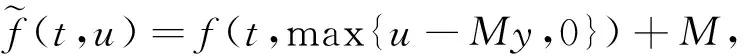

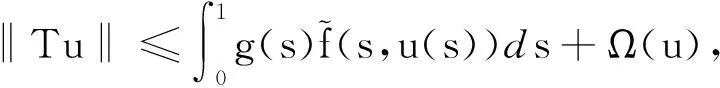


2 主要结果
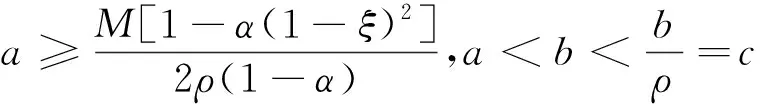
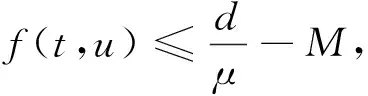



3 举例