基于稀疏沃尔什谱的BCH码检测识别方法

解 辉，宋 阳，王丰华，刘晓光

(1.国防科技大学电子科学与工程学院，湖南长沙 410073;2.解放军63893部队，河南洛阳 471003)

0 引言

随着现代通信系统中越来越多的采用信道编码技术实现系统快速稳定通信，信道编码的盲识别日益成为信息截获、信息对抗及通信协议分析等领域的热点问题［1～12］。

BCH码是能够纠正多个随机错误的二进制循环线性分组码，具有较强的纠错能力和严格的代数结构，同时具有构造方便、编码简单的优点［13］，已经广泛应用于现代数字通信系统中。对于BCH码的盲识别，目前主要有 Valembois 算法［10，11］、迭代译码算法［12］、基于码重分布［14］、基于欧几里得算法［15］和基于码根信息差熵和码根统计［16］的识别方法。Valembois［10］利用最大似然求解码字对偶码的方法，实现二进制线性分组码的盲识别，但该方法的不足之处在于计算量较大［17］。Cluzeau［12］利用 Gallager迭代算法实现了码字对偶码的快速求解，但同样要求码字具有较低的码重。文献［14］利用码重量分布估计码长，进而通过改进传统的矩阵化简方法获得生成矩阵，算法适应范围局限于低码率分组码，限制了算法的实际应用范围。算法［15］假定码长已知或码长未知而帧长度已知，采用欧几里得算法，虽然算法计算量小，但该方法误码适应能力较弱，实用性不强。文献［16］利用码根信息差熵函数识别BCH码的码长，进而利用码根统计获取生成多项式的整数根，通过遍历该域中的本原多项式以寻求满足BCH码生成多项式根性质的码根和本原多项式，从而实现BCH码的盲识别。算法需要遍历BCH码本原域，且求解码根计算量较大。

实际应用中，侦收的数据误码率往往较高，因此有必要进一步研究高误码率条件下的BCH码识别方法。利用沃尔什谱可以有效实现高误码环境下的卷积码和 Reed-Muller 码的盲识别［18，19］，但算法对存储空间和计算量都提出了很高的要求。针对BCH码的盲识别问题，提出了基于稀疏沃尔什谱的识别方法，通过BCH码校验矩阵的分布特点，只计算码字极少部分的沃尔什谱，极大减少了算法的计算量，同时利用沃尔什谱良好的误码适应特性，能够快速检测识别数据中的BCH编码，且保持较强的误码适应能力。

1 BCH码识别数学模型

(n，k)BCH码的编码过程可以表示为v=m·G［13］，其中m为k维二进制信息向量，v为n维二进制编码向量，G为生成矩阵

G的左边是一个k×k阶单位矩阵，右边是一个k×r阶矩阵，r=n－k，因此矩阵G的秩为k。若分别用Ik和P表示G的两个矩阵块，则生成矩阵G可表示成G=［IkP］。

且对于任何一个码字v都满足H·vT=0，H为校验矩阵

则矩阵H可以写成H=［PTIr］，不难看出，G与H可以互为转化。BCH码的盲识别就是通过编码向量v，通过H·vT=0求解H，进而获取编码矩阵G，并最终通过译码得到信息序列m。

2 基于沃尔什谱的BCH码识别方法

利用沃尔什谱可以求解H·vT=0方程组［18，19］，若方程组系数矩阵为满秩，则方程组只有1组解，但此时矩阵的秩为 k，方程组解的个数为2n－k，而校验矩阵为其中的n－k组解组成，其余解则为这n－k组解的线性组合。100组(15，11)码的沃尔什谱如图1所示。

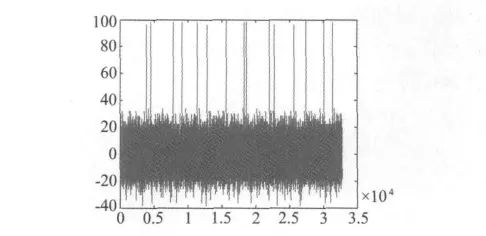
图1(15，11)BCH码的沃尔什谱

其中的峰值所在位置转化为二进制向量即为方程组的解，除去0解，共15组解，为

对H进行高斯约旦三角化，将其右边化为单位矩阵可得到校验矩阵H，为

由此可推出生成矩阵G，从而实现BCH码的盲识别。

但随着码长的增加，所需的存储空间和计算量呈指数增加，在实际中难以应用，因此提出了基于稀疏沃尔什谱的识别方法。

3 稀疏沃尔什谱的计算方法

考虑一个使m维二进制向量um满足um·B=0的解时，可以将um化为十进制数u，在2m×2m的Hadamard矩阵A中找出第u+1行，该行为1元素的位置p的二进制表示的向量p就是方程的解。上述求解过程可以用式(5)表示。

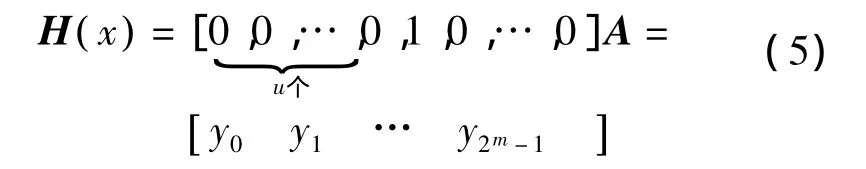
任意大小的一个Hadamard矩阵都可等分为4个区间，其中3个区间的值一致，而1个区间的值与其他3个区间的值相反。所以Hadamard矩阵中任意位置的值都可由1不断翻转获得。下面给出求解Hadamard矩阵中任意位置值的算法。

输入:Hadamard矩阵的行列值x，y;

输出:Hadamard矩阵x行、y列的值ω。

算法步骤:

(1)计算Hadamard矩阵维数m

(2)将x，y分别减1后转化为m维二进制向量xm，ym;

(3)初始 ω=1，i从1～m，如果

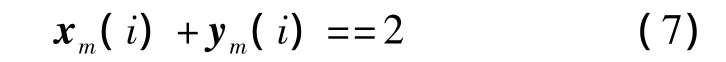
ω=－ω，否则，ω=ω。最后输出 ω就是 Hadamard矩阵x行、y列的值。

如计算Hadamard矩阵中12行、13列的值，其减1后的二进制向量分别为1 011和1 100，向量只有最高位相加为2，所以只将1翻转1次，最终12行、13列的值为－1。

4 基于稀疏沃尔什谱的BCH码识别方法

对于BCH码的盲识别，其实无需计算出整个码字的沃尔什谱，而只需要计算出峰值可能出现位置上的沃尔什谱，并根据计算的谱值大小来进行判定是否存在BCH编码。因此，BCH码的盲识别只需要先估计出编码长度，然后遍历该码长下的各种码率，并求解其校验矩阵所在位置的沃尔什谱即可，而不同码率BCH码的校验矩阵可预先进行存储。

对于BCH码的码长估计，首先给出文献［20］中的假设条件，即编码信息序列虽然未知，但其中0、1的概率分布存在一定的统计偏差，即Pr［xt=0］=1/2+ε，ε不为0。根据经典的ASCII编码，其典型值在0.05和0.1之间。文献［17］利用码字与对偶码乘积的分布概率，给出了一种Canteaut-Chabaud算法。通过对接收的码字序列进行不同长度的分组，如果分组长度恰为码字长度n，则分组后的码字矩阵与对偶码的乘积为以(M/2)［1－(1－2τ)w］为中心的二项分布，否则为以(M/2)为中心的二项分布。其中，M表示分组数量，w为对偶码字重量，τ为信道转移概率。在两种分布的峰值中间设定检测门限T，通过检测门限进行码字长度的判定。文献［17］利用Canteaut-Chabaud算法求解码重为w的对偶码，解决了码字长度的盲估计问题。

在文献［17］算法实现码字长度估计的基础上，利用稀疏沃尔什谱实现BCH码的码率及其他参数的估计。

基于稀疏沃尔什谱的BCH码识别方法可概括如下。

输入:接收码元序列;

输出:BCH码长n、信息长度k、生成矩阵G。

算法步骤:

(1)遍历码长n，对接收码元序列按长度n进行码字划分，得到码字矩阵V;

(2)利用Canteaut-Chabaud算法求解对偶码h，利用Vh与检测门限T的比较实现码字长度的快速估计;

(3)在正确码长n值内遍历其中的码率k/n，读取其码率下的校验矩阵H;

(4)求解矩阵V在校验矩阵H所在位置的稀疏沃尔什谱，并求和;

(5)将所有求解的沃尔什谱值进行差分后检测峰值，如存在峰值，则根据峰值所在位置对码长和码率进行判定，并将其校验矩阵H转化为生成矩阵G;如不存在峰值，则不存在BCH码，退出检测。

5 算法仿真及性能分析

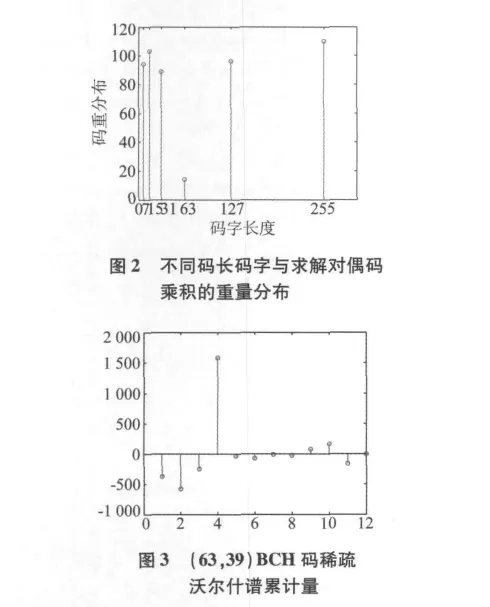
取200组误码率为1%的(63，39)BCH码进行仿真试验。将编码按各种码长进行码字划分，利用文献［17］方法估计码字长度，如图2所示，当分组长度为63时，得到码字与对偶码乘积的码重最小，由此可判定码长为63。遍历码长为63的所有码率，见表1;求解不同码率对应的稀疏沃尔什谱累积量，如图3所示。从图3中看出，在第4个谱值处出现了明显峰值，根据表1可以判定此码为(63，39)BCH码。

表1 码长为63的BCH码对应码率

针对不同码长，在不同误码率情况下对200组码字进行1 000次蒙特卡洛仿真试验，各种码长BCH码的误码率与正确识别概率的曲线图，如图4所示。

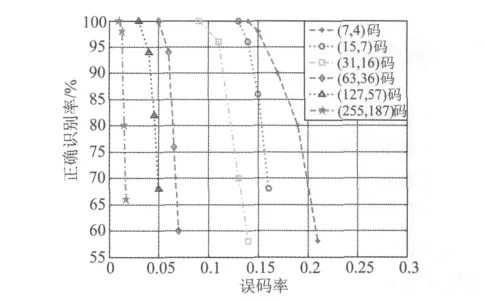
图4 不同码长BCH码的误码率与正确识别率曲线

从图4中可以看出，随着码长的增加算法的误码适应能力逐渐减弱，在相同误码率下，码长增加时，码块中出现误码的概率则越大;当误码增大时，算法中长码的适应能力则最先下降。(255，187)码在误码为1%时的检测概率可达100%，码长不超过31的短码误码适应能力都超过了10%。

分别取200组各种长度的BCH码，对文献［10，12，15，16］和本文提出的算法进行比较。各种算法的误码适应能力，如图5所示，图中的误码适应能力以正确识别率在90%以上为准，可以看出，迭代译码算法［12］与欧几里得算法［15］误码适应能力较弱，码根统计算法［16］与 Valembois算法［10］性能较好，本文提出的算法误码适应性能优于目前文献已有算法。

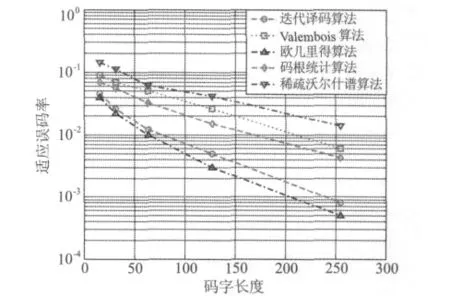
图5 不同算法的误码适应能力曲线

在计算量方面，假设BCH码长为n，信息长度为k，欧几里得算法的计算复杂度为O(n)，迭代译码算法与其计算复杂度相当。而码根统计算法的计算复杂度为O(n3)，Valembois算法在查找对偶码时计算量为O(nw/2)［17］，w为对偶码重量。本文算法的计算量主要体现在获取Hadamard矩阵的任意一点和谱值累加上，计算量为(1/2)n(n－k)，计算复杂度为O(n2)。因此，本文提出的算法计算量高于欧几里得算法与迭代译码算法，而小于码根统计算法和Valembois算法。

6 结语

针对较高误码条件下BCH码的盲识别问题，提出了一种基于稀疏沃尔什谱的BCH码检测识别算法。该算法有效利用了沃尔什谱良好的误码适应性，同时对沃尔什谱进行了稀疏求解，有效减少了算法的计算量。仿真结果表明，该算法的误码适应性能优于目前文献中已有算法，能够在较高误码率条件下实现对BCH码的盲检测与识别，且算法计算量小，易于工程实现。

［1］VINCK A J HAN，DOLEZAL PETR，KIM YOUNG-GIL.Convolutional Encoder State Estimation［J］.IEEE Transactions on Information Theory，1998，44(4):1 604-1 608.

［2］STEINBERG YOSSEF.Coding and Common Reconstruction［J］.IEEE Transactions on Information Theory，2009，55(11):4 995-5 010.

［3］COTE MAXIME，SENDRIER NICOLAS.Reconstruction of Convolutional Codes from Noisy Observation［C］//IEEE International Symposium on Information Theory，Seoul，Korea，2009:546-550.

［4］DINGEL JANIS，HAGENAUER JOACHIM.Parameter Estimation of a Convolutional Encoder from Noisy Observations［C］//IEEE International Symposium on Information Theory，France，2007:1 776-1 780.

［5］WANG FENG-HUA，HUANG ZHI-TAO，ZHOU YI-YU.A Method for Blind Recognition of Convolution Code Based on Euclidean Algorithm［C］//IEEE International Conference on Wireless Communications，Shanghai，2007:1 414-1 417.

［6］CLUZEAU MATHIEU，FINIASZ MATTHIEU，TILLICH JEAN-PIERRE.Methods for the Reconstruction of Parallel Turbo Codes［C］//IEEE International Conference on Information Theory，Austin，Texas，U.S.A，2010:2 008-2 012.

［7］CLUZEAU M，FINIASZ M.Reconstruction of Punctured Convolutional Codes［C］//Information Theory Workshop 2009:75-79.

［8］COTE MAXIME，SENDRIER NICOLAS.Reconstruction of a Turbo-Code Interleaver from Noisy Observation［C］//IEEE International Symposium on Information Theory Proceedings(ISIT)，Austin，Texas，U.S.A，2010:2 003-2 007.

［9］CHOQUEUSE VINCENT，YAO KOFFI.Blind Recognition of Linear Space Time Block Codes［C］//IEEE International Conference on Acoustics，Speech and Signal Processing(ICASSP)，2008:2 833-2 836.

［10］VALEMBOIS ANTOINE.Detection and Recognition of a Binary Linear Code［J］.Discrete Applied Mathematics，2001，111:199-218.

［11］CHABOT CHRISTOPHE.Recognition of a Code in a Noisy Environment［C］//IEEE International Conference on Information Theory，Nice，France，2007:2 211-2 215.

［12］CLUZEAU MATHIEU.Block Code Reconstruction Using Iterative Decoding Techniques［C］//IEEE International Conference on Information Theory(ISIT)，Seattle，USA，2006:2 269-2 273.

［13］LINT J H VAN.Introduction to Coding Theory［M］.Springer-Verlag Press，2003.

［14］陈金杰，杨俊安.基于码重信息熵低码率线性分组码的盲识别［J］.电路与系统学报，2012，17(1):41-46.

［15］WANG JIAFENG，YUE YANG，YAO JUN.A Method of Blind Recognition of Cyclic Code Generator Polynomial［C］.Wireless Communications Networking and Mobile Computing(WiCOM)，2010:23-25.

［16］杨晓静，闻年成.基于码根信息差熵和码根统计的BCH码识别方法［J］.探测与控制学报，2010，32(3):70-73.

［17］CLUZEAU MATHIEU，FINIASZ MATTHIEU.Recovering a Code's Length and Synchronization from a Noisy Intercepted Bitstream［C］//IEEE International Conference on Information Theory(ISIT)，Seoul，Korea，2009:2 737-2 741.

［18］刘健，王晓君，周希元.基于Walsh-Hadamard变换的卷积码盲识别［J］.电子与信息学报，2010，32(4):884-888.

［19］KANG I S，LEE H.Reconstruction Method for Reed-Muller Codes Using Fast Hadamard Transform［C］//13th International Conference on Advanced Communication Technology(ICACT)，2011:793-796.

［20］LIU XIAO-BEI，KOH SOO NGEE，WU XIN-WEN.Reconstructing a Linear Scrambler with Improved Detection Capability and in the Presence of Noise［J］.IEEE Transactions on Information Forensics and Security，2012，7(1):208-218.