小波包变换在风力发电机转子断条故障诊断中的应用
2013-11-09杨明莉刘三明王致杰丁国栋
杨明莉, 刘三明, 王致杰, 张 卫, 丁国栋
(上海电机学院 a. 电气学院, b. 数理教学部, 上海 200240)
小波包变换在风力发电机转子断条故障诊断中的应用
杨明莉a, 刘三明b, 王致杰a, 张 卫a, 丁国栋a
(上海电机学院 a. 电气学院, b. 数理教学部, 上海 200240)
将小波包变换应用于风力发电机转子故障诊断中,用Matlab小波分析将转子断条故障情况下定子侧的电流模拟信号进行多层小波分解,提取转子断条故障的故障特征,并与傅里叶分析结果对比,得到一种简易的故障诊断方法。结果表明,该方法能够准确提取故障特征,是一种优良的信号特征提取方法。
小波包; 转子断条; 故障诊断
电动机在风力发电机系统中占据重要位置。在生产制造过程中,由于遗留的安全隐患和运行中的疲劳损坏,以及受启动、过载运行中强大的热负荷电磁应力冲击的影响,使转子成为电动机故障的常发区域,其中,转子断条故障是较常见的故障之一。当电动机发生轻微断条故障时,征兆是不易被察觉的;此时,若电动机继续运行,转子就会因相邻导体内不断增加的电流引起的机械、热应力等而使断条故障扩大,导致电动机烧毁,甚至整机报废,使整个风电机组处于瘫痪状态。因此,非常有必要对转子断条故障进行研究,及时发现故障,消灭故障。
小波变换的概念是由Morlet在1974年最先提出;1986年Meyer等建立了构造小波基的方法及多尺度分析方法;比利时数学家Daubechies的《小波十讲(Ten Lectures on Wavelets)》则更加深入了对小波的认识[1-3]。小波分析是对信号时域和频域的局部变换,故能有效提取信号信息。转子在断条故障的初期,由于其故障特征中频率的分量相对于基频分量的值很小,加之,电动机在平稳运行时转差率的值也很小,故对电流信号进行傅里叶分析时,会因分辨率不足而无法有效识别故障特征。小波分析克服了传统的傅里叶分析的缺点,尤其是当信号为非连续的时变信号时,小波分析能够将信号的局部特征进行放大,且实现时域和频域的结合。本文将小波分析应用于转子故障诊断,提取转子断条故障的故障机理,得出一种行之有效的基于定子电流小波分析的转子断条故障诊断方法。
1 故障信号特征的小波包分解提取
1.1小波包算法
时域信号的小波变换可表示为
wF(a,b)=〈F,ψa,b〉=
(1)
式中,Wf(a,b)为小波变换后的信号;F(t)为原始信号;R为信号小波变换的范围区间;b为移动因子;a为尺度因子;ψ(t)为小波基函数。b与信号变化的时间有关,a与信号变化的幅度有关;通过两者的结合,能有效实现信号在特定时间段的放大,从而观察特定时刻的信号特征,或确定故障发生的准确时刻[4]。
对于给定信号F(x)的离散二进制小波变换可表示为
Cj,k=W(2j,2jk)=
(2)
式中,W(2j,2jk)为信号F(x)的离散小波变换,其中,j、k∈N;尺度因子为2j,平移因子为2jk。
当式(2)中的各尺度因子之间和各位移因子之间相互正交时,上述的变换即为正交小波变换。
小波包就是函数族。在正交小波变换对尺度空间进行分解的基础上,对小波空间进行进一步分解,使正交小波在变换中,频谱窗口随j的增大而变宽,且变得更细,从而找到最适于信号分析的时频窗口,即最优基。
本文先用Matlab小波分析工具箱对转子故障电流信号进行db小波包分解,得到信号的最优分解树,找到最能表现该信号特征的分解树节点;然后,用Matlab编程对信号进行db小波包分解,在最优节点处对信号进行小波包分解系数重构,发掘故障信号特征。
1.2故障信号特征提取方法
目前,电动机的故障诊断已发展为将信号、建模、知识相结合的智能诊断[5]。本文将电动机转子的正常工作电流和故障电流信号分别进行小波包分解,找出最能表现出信号特征的小波分解树的节点;然后,对该节点做相应的小波包分解系数重构,发现信号与非故障信号的异同点,提取故障特征[5]。诊断过程图如图1所示。
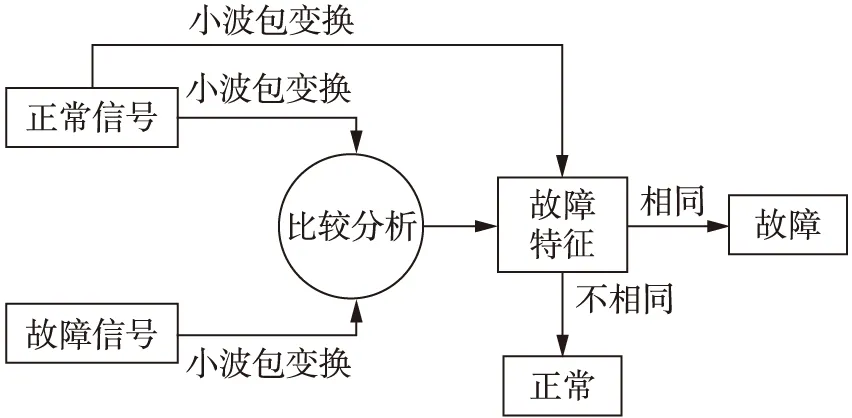
图1 故障信号特征提取流程Fig.1 Fault signal feature extraction
2 故障信号的建模与仿真
2.1故障信号建模
Jufer 用数学公式推导证明了电动机发生转子断条故障会对转子电流产生调制影响,即转子电流中会出现(1±2S)f的频率分量[6-8],其中,f为工频电源频率,S为电动机的转差率。根据转子发生断条故障时其定子电流的特点,构造其动态仿真模型,则此时定子侧电流为
i(t)=s(t)+x(t)=A1cos(2πfn/fs)+
A2cos[2π(1±2S)fn/fs]
(3)
式中,s(t)为电源频率信号;(x)t为转子断条故障特征频率信号;A1为工频电源电流信号的幅值;A2为断条故障时定子电流故障特征分量的幅值,通常,0lt;A2/A1lt;0.03,本文中A1=1,A2=0.02;f=50Hz;n为采样点数值,本文中n=1024;fs为采样频率,fs=500Hz;S=0.01。因此,转子正常及故障情况下的定子侧电流的动态仿真模型为
s1=sin (100πt)
(4)
s2=sin (100πt)+0.02sin (98πt)+0.02sin (102πt)
(5)
在电动机发生转子断条故障的初期,定子侧电流频率中的故障特征分量(1±2S)f相对于工频分量的值很小,加之电动机在稳定运行的情况下,S很小,则此时定子侧电流的特征频率(1±2S)f与f近似相等[9-13]。若直接对转子断条故障情况下的定子侧电流进行傅里叶分析,则会因分辨率不足而不易发掘故障特征,故本文采用小波包分析来发掘转子断条故障特征。
2.2仿真结果与分析
在Matlab中通过编程对转子正常及故障情况下的电流信号进行傅里叶变换,得到如图2、3所示的仿真结果。由图2、3可见,当转子无故障时,其定子侧电流信号的傅里叶分解时序图中没有叠加正弦信号的迹象,频域图中也未出现频率边频调制现象[14-18];而当转子发生断条故障时,其电流动态仿真模型的傅里叶分解图中会出现小正弦信号叠加现象,且频域图中在50Hz处出现轻微边频调制现象。
与图2相比较,图3只有少许不同,这是由于仿真是在S=0.01时进行的,S值越小,两者的差别越小,甚至肉眼无法发现[13-14];若在转子轻微断条故障的初期,两图的差别将无法在傅里叶分解图中体现。


图2 转子无故障电流信号的傅里叶分解图
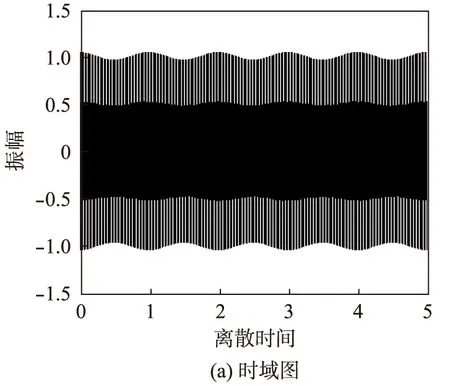
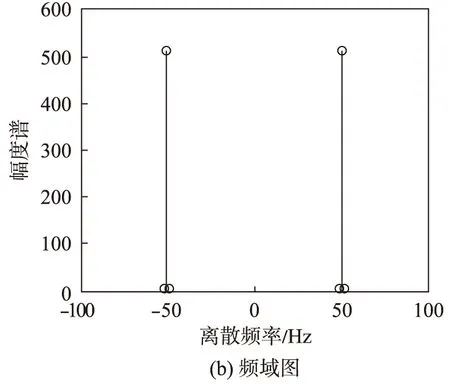
图3 转子断条故障时定子电流信号的傅里叶分解图
将信号s1和s2分别加载到Matlab小波分析工具箱中,对转子断条故障情况下的信号进行小波包分解,得到其最优小波包分解树和彩色节点系数图,如图4所示。将鼠标放置在彩色节点系数图颜色最深处,单击鼠标右键,则在左下方显示此处颜色代表的信号小波包分解节点。如将鼠标放在图4(b)中最红色处(见图中R处)单击右键,则下方显示节点数为(5,9),该处分辨率最高,故该节点最能体现被分解信号的细微特征。


图4 转子段条故障时定子电流信号的小波包分解图
找到转子断条故障信号的最优分解节点后,再编程分别对正常和转子断条故障情况下的定子侧的电流信号进行db5五层小波包分解,并在节点(5,9)处对被分解信号进行小波包重构,得到如图5所示的仿真结果。它是对图3(b)中较难识别的边频现象进行放大再现,可以确定转子断条故障的特征频率为50Hz,且证明转子断条故障会对定子侧电流产生调制影响。

图5 在节点(5,9)处的小波包分解系数重构图Fig.5 Composition of wavelet packet decomposition coefficient at node (5,9)
3 结 语
本文用电流模型对风力发电机转子断条故障进行模拟仿真,提取转子断条故障特征。为了克服在转子断条故障的初期因故障特征频率分量与基频相差很小、在傅里叶分解图中因分辨率不足而不易被察觉的缺点,提出用小波包分解重构的方法来发现转子断条故障,并在转子断条故障的初期有效地察觉了故障特征。同时,也证明了信号的小波包分解系数重构法是发现信号细微特征的有力工具。如果检测的原始信号为故障信号,则最终得到故障信号特征,该法即为故障特征检测方法;如果得到的信号特征为噪声信号,则用相应的滤波方法去除该细微信号,即得到信号去噪方法;如果利用此法检测原始信号特定频率的信号特征,该法即为信号特征提取方法。
[1] Goswami J C,Chan A K.小波分析理论、算法及其应用[M].许天周,黄春光,译.北京: 国防工业出版社,2007: 11-20.
[2] 葛哲学,沙 威.小波分析理论与MATLAB R2007实现[M].北京: 电子工业出版社,2007: 282-285.
[3] 何正嘉,訾艳阳,张西宁.现代信号处理技术及工程应用[M].西安: 西安交通大学出版社,2010: 6-10.
[4] Gritli Y,Rossi C,Zarri L, et al.Advanced diagnosis of broken bar fault in induction machines by using discrete wavelet transform under time-varying condition[C]∥2011 IEEE International Electric Machines amp; Drives Conference. Niagara Falls,ON:IEEE,2011: 424-429.
[5] Mariun N,Mehrjou M R,Marhaban M H,et al.An experimental study of induction motor current signature analysis techniques for incipient broken rotor bar detection[C]∥2011 International Conference Power Engineering,Energy and Electrical Drives.Malaga: IEEE,2011: 1-5.
[6] Kechida R,Menacer A.DWT wavelet transform for the rotor bars faults detection in induction motor[C]∥2011 2nd International Conference on Electric Power and Engergy Conversion Systems.Sharjah: IEEE,2011: 1-5.
[7] Bouchikhi E H E,Choqueuse V,Benbouzid M E H.Current frequency spectral subtraction and its contribution to induction machines’ bearings condition monitoring[J].IEEE Transactions on Energy Conversion,2013,28(1): 135-144.
[8] 魏云冰.小波变换在电机故障诊断与测试中的应用研究[D].杭州: 浙江大学,2002: 22-25.
[9] 姜小荧.基于小波分析的滚动轴承故障诊断方法的研究及应用[D].大连: 大连理工大学,2005: 18-23.
[10] Arabaci H,Bilgin O.Diagnosis of broken rotor bar faults by using frequency spectrum of stator current envelope[C]∥2012 XXth International Conferenceon Electrical Machines.Marseille: IEEE,2012: 1643-1646.
[11] 崔宝珍.基于小波分析的滚动轴承故障诊断方法研究与应用[D].太原: 中北大学,2005: 112-115.
[12] 龚海鹏.小波变换在转子故障诊断中若干问题的研究[D].上海: 上海交通大学,2008: 35-37.
[13] 张 楠,刘占生,姜兴谓.转子-轴承系统局部碰摩故障机理研究[J].轴承,2010(8): 29-34.
[14] Kaikaa M Y,Hadjami M,Khezzar A.Effects of the simultaneous presence of static eccentricity and broken rotor bars on the stator current of induction machine[J].IEEE Transactions on Industrial Electronics,2013,61(5): 2452-2463.
[15] 刘蕾蕾.基于小波分析的电机故障信号诊断研究[D].哈尔滨: 哈尔滨理工大学,2007: 32-33.
[16] 时建峰.基于时、频域-小波分析和神经网络方法的齿轮箱故障诊断研究[D].太原: 太原理工大学,2008: 48-51.
[17] Abitha M W,Rejini V.Induction motor fault diagnosis using labview[C]∥2013 International Conference on Circuits,Power and Computing Technologies.Nagercoll,India: IEEE,2013: 176-179.
[18] 杨江天,赵明元,张志强,等.基于定子电流小波包分析的牵引电机轴承故障诊断[J].铁道学报,2013,35(2): 32-37.
Application of Wavelet Packet Transform to Diagnosis of Broken Bar in Wind Turbine Rotor
YANGMinglia,LIUSanmingb,WANGZhijiea,ZHANGWeia,DINGGuodonga
(a. School of Electric Engineering, b. Department of Mathematics and Physics, Shanghai Dianji University, Shanghai 200240, China)
Wavelet packet transform is applied to wind turbine rotor fault diagnosis in this paper. The analog current signal on the stator side in the rotor under a broken bar condition is decomposed into multiple layers using wavelet analysis to extract features of the fault. Comparing with the Fourier analysis results, a simple method of fault diagnosis is obtained. The results show that the method can accurately extract the fault characteristics, giving a good signal feature extraction method.
wavelet packet; rotor broken bar; fault diagnosis
2095-0020(2013)05 -0272-05
TM 315.07
A
2013-05-05
国家青年自然科学基金项目资助(1120126);上海市自然科学基金项目资助(12ZR1411600)
杨明莉(1990-),女,硕士生,主要研究方向为大规模新能源电力设备安全策略,E-mail: 310177194@qq.com
