双因素方差分析在地球化学数据处理中的应用

李昱星

（长安大学地球科学与资源学院 陕西西安 710054）

在地球化学的数据处理与分析中经常需要知道矿产品味，规模，分布状况的是哪些因素影响，并且需要知道哪些因素影响效果显著，而哪些因素是可以被忽略的，这样可以提供下一步的找矿依据，以及对产的规模，分布有更加准确的预测。

本文选用如下实例描述如何利用双因素方差分析来处理地球化学数据。

某地区不同岩性的土壤L1,L2,L3按照不同深度D1,D2,D3取样化验，L、D的每一组合取5个样品，共45个个样品（如下表1），用方差分析研究不同岩性和不同深度取样对铜含量的影响。

1 建立数学模型

I在进行地球化学的研究中，可以知道在不同的岩性，不同的深度，不同的构造下金属Cu的含量可能是不同的，在这次模型的建立中选择了两个因素：岩性、深度，需要同时考虑岩性和深度对金属Cu的含量是否能造成影响，可以建立基本的模型。

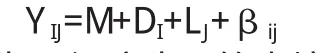
其中YIJ为在岩性为I，深度为J的土壤中取得的地球化学样中金属Cu的含量，M为样品中Cu含量的平均值，DI为由于岩性引起的Cu含量的异常，Lj为由于样品取样深度引起的Cu含量的异常。βij为由于随机因素导致的异常。

但是以上双因素的模型并不严谨，因为可能出现如下状况：比如深度是否能够体现出异常要看岩性具体是什么类型；或者岩性是否能体现出异常，要看具体的取样深度而定。这种状况被称为两个因素存在交互作用，此时需要在模型中加入交互项。

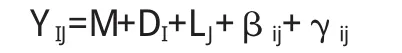
这里的γij表现的是岩性为j，深度为i时两者的交互作用。

在数学建模时未考虑每组合的多次取样，可以比较清楚的建立较为简单易懂的模型。

II对模型中效应的检验：

建立好模型后，要对岩性和深度这两个因素对Cu含量的作用进行检验，根据上面模型的公式，可以将总的样本离均差的和分解成几部分：SS总=SS岩性+SSD深度+SS误差，然后用每个离均差平方和除以自由度就可以得到均方，例如：MS岩性=SS岩性/DF岩性，最后将各效应的均方与误差的均方相比较就得到了F统计量，例如F岩性=MS岩性/MS误差。借助F分布，就可以知道岩性和深度对Cu的含量有多大的影响。

2 用spss进行双因素方差分析

Excel，spss和matlab都可以实现双因素方差分析，在实验中发现spss较为简单易用，下面演示spss如何进行处理。

首先要对给定的数据在EXCEL中进行处理，处理为如表2格式，按照岩性和深度两个因素进行排列

spss中不需要单独设置多次取样为变量,只需要用数字1,2…5区分不同次数的取样.

选择菜单:分析->一般线形模型->单变量(本例中只有一个因变量Cu)。首先要进行变量设置：在这里将Cu含量设置为待分析的因变量，将深度和岩性设置为固定因素接下来是进行选项设置和选择：

A：模型选项

模型选项中主要是使用模型的类别，默认是全因子，也可以自己设定。这里全因子包括了所有因素变量对Cu的含量的影响，因为本文中考虑的是岩性和深度的交互作用对Cu含量的影响，故选择主因子，否则可以在设定中选择主效应。

B：选项设置

在这个选项中首先要注意到的是要首先设置显著性水平，本例中为a=0.05，即置信区间为95%，其次要对数据进行方差齐性检验。数据符合正态分布和近似正态分布是做方差分析的基本条件，而在方差分析的F检验中，是以各个实验组内总体方差为齐性为前提的。本文数据经检验SIG值为0，方差奇性，分析具有统计学意义。最后选定的参数有描述统计，方差齐性检验，检验效能三项

3 结论分析

图表参数解释：S岩性=1022.896，S深度=0.1，S岩性*深度=0.396，S误差=4.236；DF为个因素自由度，其中岩性，深度为2，岩性*深度为4，误差为36，均方为个因素条件误差值昱其自由度的比值。F为各要素统计量。

SIG值为显著性检验值：

岩性的SIG值<0.05,所以在0.05的显著水平上认为其方差是显著的，即岩性不同的情况下土壤中Cu的含量变化很大，深度以及深度*岩性的SIG>0.05,所以在0.05的显著性水平上认为其方差无显著差异，故对Cu的含量多少没有影响。由于岩性对Cu含量的显著性影响，故在做地球化学数据处理的过程中需要对不同岩性的岩石选取不同的地球化学背景值。

[1]Georege S.koch，Jr Richard F.Link.1970，STATISTICAL ANALYSISOFGEOLOGICALDATA，john wiley&sons，inc

[2]杨永国.数学地质[M].徐州：中国矿业大学出版社，2010

[3]吴锡生.化探数据处理方法[M].北京：地质出版社，1993

[4]奥特、格朗内克著；张忠占等译.统计学方法与数据分析引论[M].北京：科学出版社，2003