风场估计算法及其在组合导航中的应用

高社生, 张极, 党进伟

(西北工业大学 自动化学院, 陕西 西安 710072)

风场估计算法及其在组合导航中的应用

高社生, 张极, 党进伟

(西北工业大学 自动化学院, 陕西 西安 710072)

风场的不稳定性和随机性会严重影响无人机、飞艇等飞行器的导航定位精度,而现有的采用线性定常模型描述风场的方法会引起较大的建模误差。为了提高对风场的估计精度,在建立风场模型时将系统噪声和量测噪声假设为随机游走噪声,在状态方程中引入时变系数,建立了一种新的一阶线性时变自回归风场模型。在风场估计中采用抗差自适应滤波算法,以控制观测异常的影响,利用估计出的风场信息对SINS/SAR/CNS组合导航系统的航迹进行修正。仿真结果表明,所建立的时变风场模型能更好地描述风场信息的变化,抗差自适应滤波算法能有效抵制观测异常,提高组合导航系统的解算精度。

组合导航; 风场估计; 抗差自适应滤波; 观测异常

0 引言

风场作为一种飞行环境,不可避免地会对无人机、飞艇等飞行器的飞行品质和导航精度造成影响[1]。如何建立较为准确的风场模型,并通过滤波计算获得高精度的风场估计值,然后利用该估计值进行航迹修正,是增强飞行器抗风场干扰能力、提高导航精度的一项关键技术。

由于风场的不稳定性和随机性较大,因此很难建立准确的数学模型。当模型存在误差或系统的状态突然改变时,采用传统的Kalman滤波算法容易造成较大的误差,甚至出现滤波发散。当前在风场估计中一般将风场模型设为线性定常模型,采用Sage-Husa自适应滤波算法估计风场[2],该算法在风场环境较为平稳时滤波效果较好,但当出现剧烈扰动导致观测异常时,滤波效果较差[3]。而影响风的因素较多,在长时间、大范围的风场测量过程中,风切变、暴风以及传感器和数据传输的暂时性失效都可能导致观测数据中包含较大野值或成片野值,出现观测异常[4],从而影响导航定位精度。

本文从模型修正出发,建立系数时变、噪声为随机游走的风场模型,采用抗差自适应滤波[5-6]算法对风场进行估计,并利用估计得到的风场信息对SINS/SAR/CNS组合导航系统进行航迹修正,从而有效提高组合导航系统的导航定位精度。

1 风场模型

由于风场的随机性较大,难以用确切的数学模型描述。工程上一般采用一阶马尔可夫过程来描述平均风[2],该模型简单且容易计算,但难以充分反映风场随时间不断变化的特点。此外,模型中的噪声假设为高斯白噪声,而实际中的噪声特性往往比较复杂,经常会出现有色噪声。

本文在研究风场线性定常模型的基础上,考虑风场随机性和噪声复杂性的特点,引入时变系数,建立一阶线性时变自回归风场模型如下:

(1)

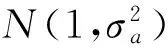
(2)

式中,wk+1和vk+1是零均值高斯白噪声,相应的协方差阵分别为Σwk+1和Σvk+1。

2 风场估计算法

2.1 有色噪声白化

在式(1)所描述的风场模型中,ηk和γk均为有色噪声,需要将其白化。

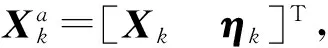
(3)

采用观测值差分法对观测噪声γk进行白化处理。

(4)

将扩维后的状态方程代入式(4)得:

(5)

Hk+1Γkwk+1+vk+1

(6)

则新的观测方程为:

(7)

式中,Lk为噪声白化后新的观测向量;Ak为新的观测阵;ek为新的观测噪声。有如下关系:

Lk=Zk+1-Zk

(8)

Ak=Hk+1Φk+1,k-Hk

(9)

ek=Hk+1Γkwk+1+vk+1

(10)

由于E[ek]=Hk+1ΓkE[wk+1]+E[vk+1]=0,故ek是零均值的白噪声。ek的协方差阵为:

(11)

2.2 系统噪声与观测噪声去相关

(12)

将状态方程改写为:

(13)

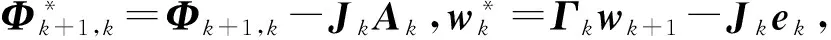
(14)

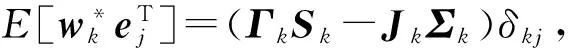
(15)

2.3 抗差自适应滤波算法

抗差自适应滤波的基本思想是:当观测值存在异常时,对观测值采用抗差估计原则;当动力模型存在异常误差时,将动力模型信息作为一个整体,用自适应因子调整动力模型信息对状态参数的整体贡献。选取k时刻的状态预测向量为:

(16)

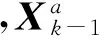
状态预测向量的协方差阵为:

(17)

状态预测向量和观测向量的误差方程分别为:

(18)

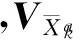
构造极值方程如下:

(19)

(20)

将误差方程式(18)带入式(20),得状态参数向量的抗差自适应滤波解为:

(21)

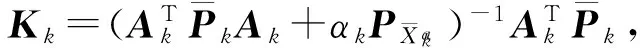
(22)

将式(22)代入式(21)可得:

(23)

状态向量的协方差阵为:

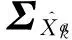
(24)

抗差自适应因子[5]取为:

(25)

式中,c0和c1为常数,c0可取1.0～1.5,c1可取3.0～8.5。

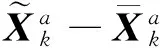
(26)

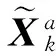
(27)

式中,等价权矩阵元素取为三段权函数[5],这里假设观测值独立。

(28)

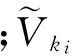
3 基于风场估计的组合导航滤波结构

风场估计的主要目的是进行航迹修正。将风场估计引入SINS/SAR/CNS组合导航系统,由SINS提供风场测量中所需的地速信息,并利用估计出的风场信息对捷联惯导输出的位置信息加以修正,以提高组合导航系统的定位精度。加入风场估计后的SINS/SAR/CNS组合导航滤波结构如图1所示。

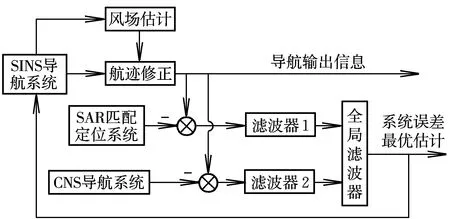
图1 加入风场估计的组合导航滤波结构Fig.1 Structure of integrated navigation filter with wind field estimation

(29)

式中,l为航迹修正步长,0≤l≤Δt。

4 仿真试验与分析

4.1 风场模拟

为了验证所建立的风场模型的合理性,比较Kalman滤波、Sage-Husa自适应滤波和抗差自适应滤波的估计效果,需要较真实地模拟出自然风。采用如下模型模拟风场[4]:

(30)

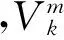
(31)

式中,σ为紊流强度;L为紊流尺度;h为采样步长。

4.2 仿真试验及结果分析

考虑到一阶线性时变自回归模型与线性定常模型的差异,通过仿真,比较Kalman滤波(KF)、Sage-Husa自适应滤波(ASF)及抗差自适应滤波(ARF)的估计精度和抗野值效果,判断本文采用的模型及算法用于风场估计的合理性及可行性。

风场模拟器的参数设置如下:

[ΣvmΣσLhvm(0)vt(0)]=

[0.01 1 1.75 100 20 10 0]

三种滤波算法的系统模型均采用本文建立的风场模型,系统噪声方差初值设置为Σw0=0.01,量测噪声方差初值设置为Σv0=2。

图2是三种滤波算法的风速估计结果。从图中可以看出,Sage-Husa自适应滤波和抗差自适应滤波均能抵制风场动态模型误差的影响,估计结果明显优于经典Kalman滤波。

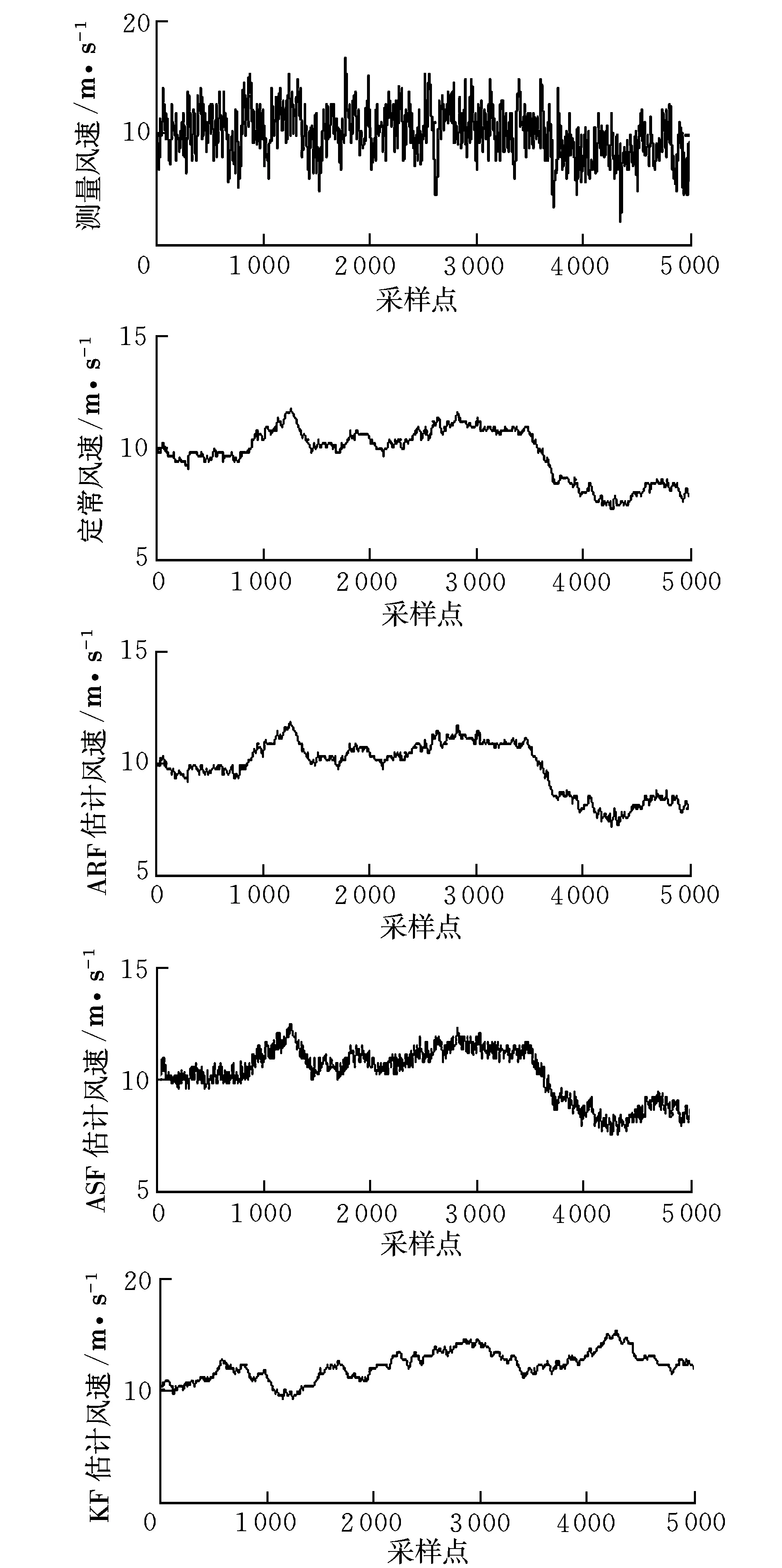
图2 三种滤波算法的风速估计值比较图Fig.2 Comparison of wind speed estimates by three different kinds of filtering algorithm

图3是引入连续野值时的风速估计结果,图4是对图3的局部放大。

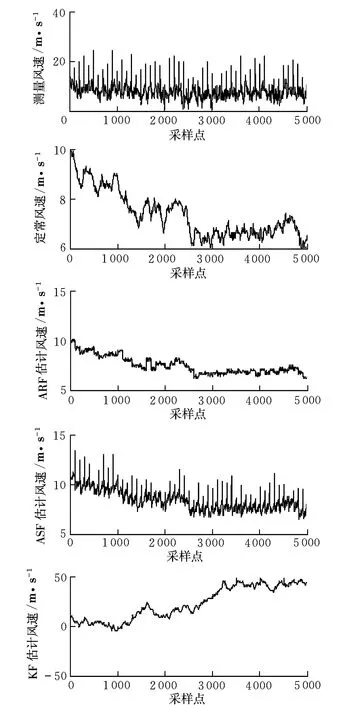
图3 加入野值后的风速估计值比较图Fig.3 Comparison of wind speed estimates joined in outliers

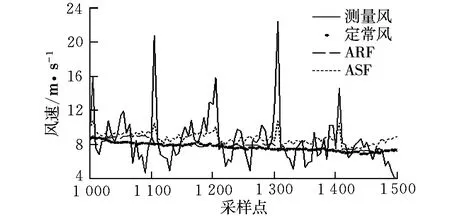
图4 加入野值后的风速估计值比较局部放大图Fig.4 Partial comparison of wind speed estimates joined in outliers

由图可见,由于大量野值的存在,Kalman滤波估计结果严重偏离状态真值,出现发散;Sage-Husa自适应滤波未采取任何措施抵制观测异常,因而对连续野值的处理效果不理想,在野值处估计结果出现跳变,滤波效果较差;而抗差自适应滤波能够实现真正意义上的“自适应”,不但灵活地抵制了动态模型噪声异常的影响,而且抵制了观测异常对状态参数估值的影响,较好地处理了野值,估计结果平稳且精度较高。

将风场估计应用于SINS/SAR/CNS组合导航系统中,组合导航系统的参数设置与文献[7]相同。图5给出了未加入风场估计与加入风场估计时的组合导航位置误差。从图中可以看出,未加入风场估计时的位置误差在10 m以内,而利用风场估计值对航迹进行修正后的位置误差减小到了5 m以内,组合导航系统的定位精度得到了明显提高。

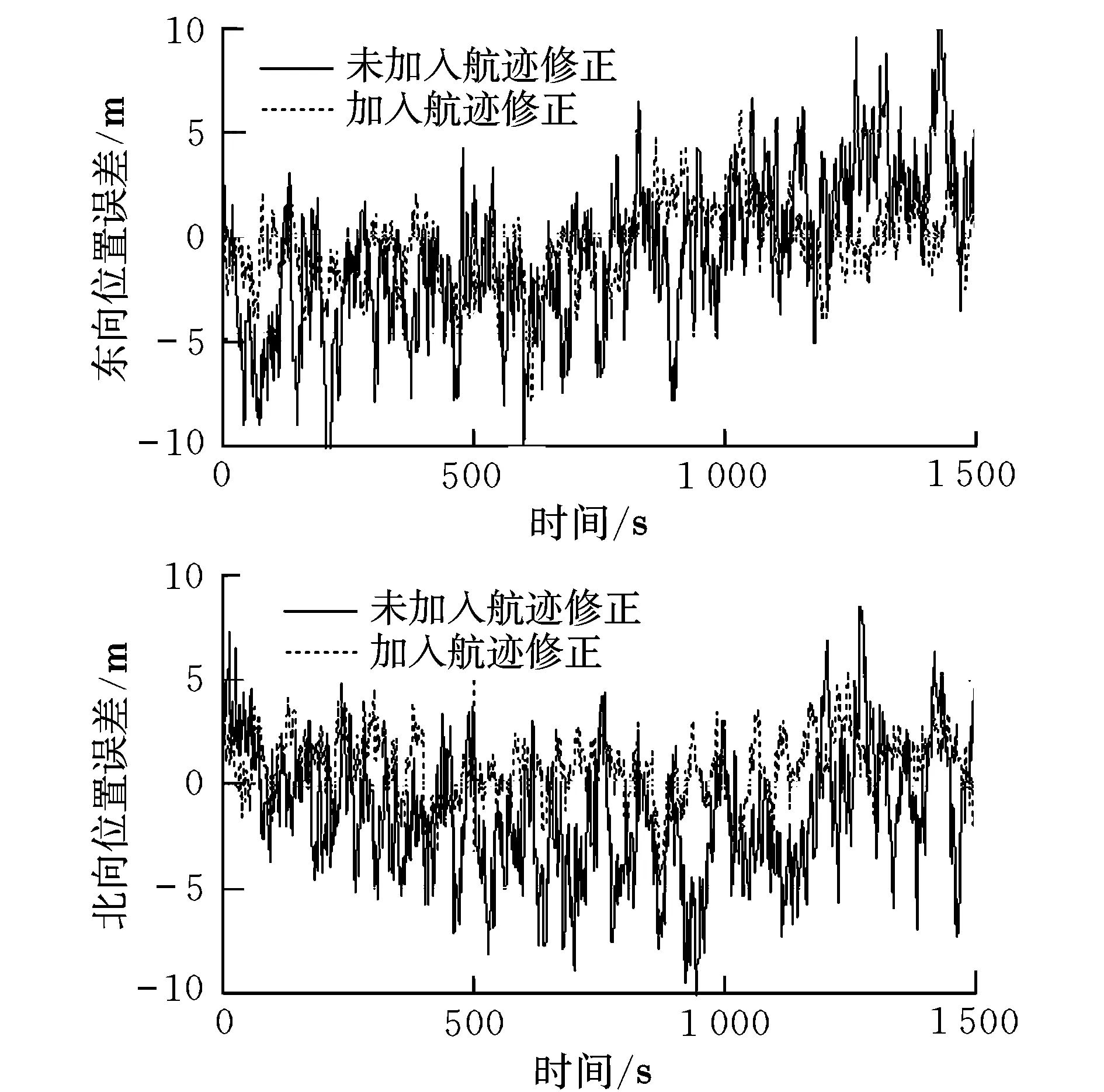
图5 组合导航位置误差曲线Fig.5 Position errors of the integrated navigation system

5 结束语

提高风场估计精度的关键是有效抵制观测异常和动态模型噪声异常的干扰。本文的研究结果表明,一阶线性时变自回归模型具有较大的灵活性和适应性,能更好地体现风场的变化,可作为线性定常模型的改进模型用于风场估计。针对此模型采用的抗差自适应滤波算法能有效抵制观测异常和动态模型噪声异常对状态参数估值的影响,与传统Kalman滤波、自适应滤波算法相比具有较强的抗野值能力,滤波结果稳定性好且精度较高。将获得的风估计值应用在组合导航系统中用以修正航迹,能够明显提高组合导航系统的定位精度。

[1] 屈耀红,凌琼,闫建国,等.无人机DR/GPS/RP导航中风场估计仿真[J].系统仿真学报,2009,21(7):1822-1825.

[2] 蔡崧,产竹旺.基于自适应滤波的风场测量仿真试验平台[J].计算机工程,2003,29(18):192-194.

[3] Yang Yuanxi,Xu Tianhe.An adaptive Kalman filter based on sage windowing weights and variance components[J].Journal of Navigation,2003,56(2):231-240.

[4] 达兴亚,周伟静,沈怀荣.基于辅助粒子滤波的风场估计方法研究[J].系统仿真学报,2008,20(22):6248-6251.

[5] Gao Shesheng,Zhong Yongmin,Li Wei.Robust adaptive filtering method for SINS/SAR integrated navigation system[J].Aerospa Science and Technology,2011,15(6):425-430.

[6] Gao Shesheng,Zhong Yongmin,Li Wei. Random weighting method for multisensor data fusion[J].IEEE Sensors Journal,2011,11(9):1955-1961.

[7] 高社生,宋飞彪,姜微微.抗差自适应模型预测滤波及其在组合导航中的应用[J].中国惯性技术学报,2011,19(6):701-705.

Windfieldestimationalgorithmanditsapplicationinintegratednavigation

GAO She-sheng, ZHANG Ji, DANG Jin-wei

(College of Automation, Northwestern Polytechnical University, Xi’an 710072, China)

The instability and randomness of wind field will seriously affect the navigation and positioning accuracy of unmanned aerial vehicles, airships and other aircraft. Describing the wind field by linear time-invariant model may introduce some modeling errors. In order to improve the estimation accuracy of the wind field, a new time-varying autoregressive model with the time-varying coefficient was established and both the system noise and the measurement noise of the model were regarded as random walk noises. The robust adaptive filtering algorithm was used to estimate the wind field to control the impact of measurement outliers. The estimates of wind field were used to correct track errors of SINS/CNS/SAR integrated navigation system. The results of simulation show that the new time-varying model can reflect the changes of the wind field better. The robust adaptive filtering algorithm has so strong ability of anti-interference that it can improve the calculating precision of the integrated navigation system.

integrated navigation; wind field estimation; robust adaptive filtering; measurement outliers

V249.3

A

1002-0853(2013)05-0467-05

2012-11-12;

2013-01-05; < class="emphasis_bold">网络出版时间

时间:2013-06-06 13:21

国家自然科学基金资助(61174193)；陕西省自然科学基金资助(NBYU0004)

高社生(1956-)，男，陕西周至人，教授，博士生导师，研究方向为导航、制导与控制。

(编辑：方春玲)