近空间飞行器再入段载荷特性分析

陈红永, 陈海波

(1.中国科学技术大学 近代力学系, 安徽 合肥 230027;2.中国科学院 材料力学行为和设计重点实验室, 安徽 合肥 230027)

近空间飞行器再入段载荷特性分析

陈红永1,2, 陈海波1,2

(1.中国科学技术大学 近代力学系, 安徽 合肥 230027;2.中国科学院 材料力学行为和设计重点实验室, 安徽 合肥 230027)

针对近空间飞行器再入段载荷问题,考虑地球曲率和自转的影响,建立飞行器六自由度动力学模型和载荷模型,进行飞行器载荷特性研究。分析了开环状态下飞行器的载荷构成,以及在大飞行包线内飞行器载荷的变化规律;考察了质量变化以及舵面控制状态下舵偏速度、最大舵偏角等因素对飞行器载荷特性的影响。研究结果表明,再入高超声速飞行器的过载分析必须考虑地球曲率和自转的影响,飞行器的过载对高度、速度和最大舵偏角敏感性强;采用重心过载在机体低速转动时可以表征飞行器全局过载,飞行器质量变化及相应的重心偏移对飞行器载荷有一定影响;不同舵偏模式及速度、角度对于整体载荷有较大影响。

近空间飞行器; 六自由度动力学模型; 载荷模型; 舵面控制

0 引言

飞行器载荷特性是弹道、结构设计的重要依据,对载人飞行器的舒适性[1-2]更有着重要的意义。近空间飞行器再入段是飞行器以高超声速无动力滑翔、通过机动动作调整姿态、利用大气阻力消耗能量减速下降的阶段,该段气动力非线性强、动压变化范围大[3],是飞行器载荷设计重点关注的一段。

进行载荷分析的基础是建立精确的飞行器气动力及动力学模型。Snell[4]建立了基于平面大地假设的飞行器六自由度动力学模型,设计了非线性动态逆控制器并进行了仿真。Keshmiri等[5]和Colgren等[6]建立了典型高超声速飞行器 (Generic Hypersonic Vehicle,GHV) 六自由度动力学模型;通过拟合实验和数值模拟数据得到了飞行器在不同阶段的气动力系数,对气动特性和动力学特性进行了分析;还考虑了气动力和推力系统的耦合,但刚体动力学模型仍采用平面大地假设。李菁菁等[3]研究了高超声速飞行器再入段控制系统的设计方法,但其动力学模型忽略了地球自转及飞行器质量的变化。Bolender等[7]考虑了离心力影响,建立了面向控制的吸气式高超声速飞行器(AHV)的非线性纵向动力学模型。鲍文等[8]建立了综合离心力/气动力的升力体高超声速飞行器刚体动力学纵向模型,进行了动力学特性分析,但忽略了六自由度之间的耦合作用。齐乃明等[9]基于GHV研究了高超声速飞行器的舵机对弹道、气动力对姿态角速度的耦合特性。但是,现有的高超声速飞行器模型多为面向控制而设计的纵向动力学模型,忽略了通道之间的耦合作用;而六自由度模型均采用平面大地假设建立,忽略了地球曲率和自转,在高超声速段误差变大,而且已有的资料中鲜有对飞行器载荷特性方面的分析。可见,对高超声速飞行器载荷分析,需要综合考虑地球曲率及自转影响,以及各通道之间的耦合及舵面控制等因素。

本文综合考察了近空间高超声速飞行器再入段各因素对载荷特性的影响,所得到的分析方法和载荷变化规律对该类飞行器设计具有重要的参考意义。

1 近空间飞行器动力学模型

本文选用某典型高超声速飞行器模型[10],仅考虑高速再入段,取Ma>5的气动力数据,描述该段飞行器完整气动力特性。

飞行器所受气动力为:

A=[DCL]T

(1)

式中,D=qSCD;C=qSCC;L=qSCL。

飞行器所受气动力矩为:

M=[MlMmMn]T

(2)

其中:

Ml=qbSCl

Mm=qbSCn+xcg(Dsinα-Lcosα)

Mn=qcSCm+xcgC

式中,xcg为飞行器质心与参考力矩中心之间的距离。

采用文献[11]的思路,考虑地球曲率和自转等非惯性因素,推导飞行器的质心动力学方程:

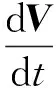
ωE×(ωE×r)

(3)

式中,ωr为坐标系之间的相对转动角速度;ωE为地球自转角速度;r为飞行器位置。式(3)右边第一项为气动力项,第三项为考虑地球曲率半径影响的地球引力项,第四项为Coriolis力项,第五项为地球自转产生的离心力项,后三项在平面大地假设下的运动方程中并不出现。将式(3)在航迹坐标系内展开,可得:

(4)

(5)

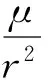
飞行器的转动方程可表示为:

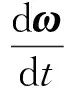
(6)

(7)

(8)

式中,ωx,ωy和ωz分别为机体绕三轴的转动角速度;Ix,Iy和Iz为飞行器的转动惯量。

2 飞行器载荷模型

按照飞行器过载定义,结合式(3)可得在航迹坐标系中飞行器的重心过载为:

ncg=[nxcgnycgnzcg]T

(9)

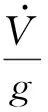
对于常规飞行器来说,由于飞行速度不高,空域范围小,故气动力项引起的过载占主导,其他项可以忽略不计。而文献[8]指出,对于高超声速飞行器,离心力等惯性力对升力的影响已经很大,故在载荷分析中,需要保留这些项。

另一方面,由于近空间飞行器尺寸较大,故需要分析除重心之外的其他位置的过载情况。定义机体上任意一点相对于飞行器重心的位置为P=[xpypzp]T,则可推出刚体飞行器上P点的过载为:

(10)

其中:

式中,右边第一项为重心过载,是航迹坐标系转化到机体坐标系的量,它包括了平面大地假设下的气动力项,以及考虑地球曲率和自转的惯性力项;第二项为机体转动产生的载荷,由离心力产生。将式(10)展开可得飞行器载荷模型为:

(11)

如果直接对该式进行偏微分求解,由于式(4)、式(5)和式(7)的复杂性,很难得到过载对于某一变量的敏感性表达式。故本文根据载荷模型,设置典型工况进行动态仿真,间接对载荷特性进行分析。

3 载荷分析

3.1 载荷构成分析

根据前面分析,可以将总过载分为气动力项、考虑地球曲率和自转等惯性力项、机体转动项三部分。由于近空间飞行器外形巨大,故首先考察飞行器不同部位由于机体转动产生的载荷分布。以Ma=10,H=30 000 m,α=2°,β=0.5°,φv=0°为典型初始状态。飞行器各典型位置由于机体转动引起的横向过载的变化如图1所示。根据式(10),相同姿态参数下飞行器各位置之间三向过载仅由位置坐标决定,故重心处作为转动中心,此项为0;头部因为远离重心,此项最大;其他各部位变化趋势相同。而总体来看,此项最大值(=0.08)明显小于同样工况下重心处总横向过载(=1.9),在载荷设计时一般可以忽略。故在以下分析中以重心处过载表征整体过载。

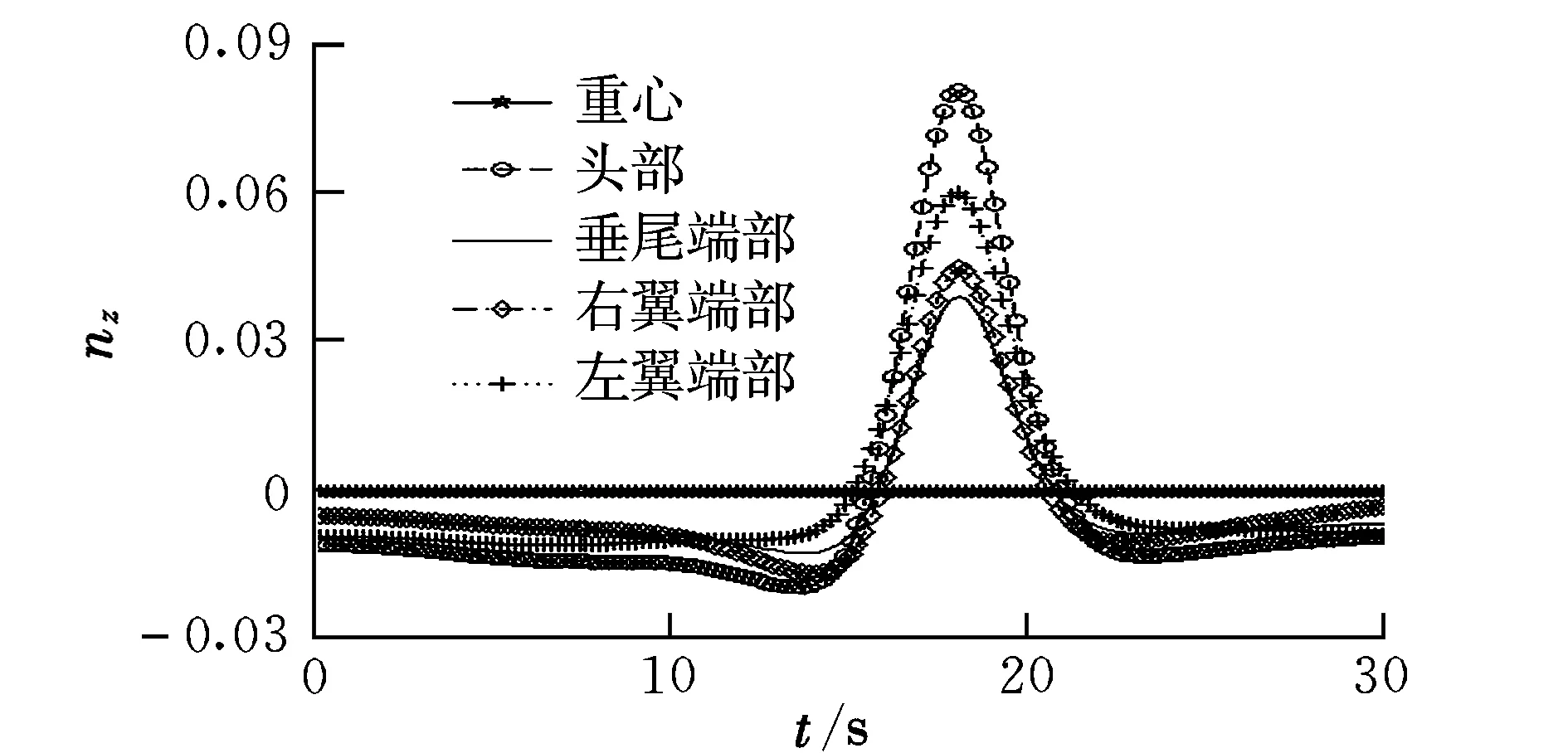
图1 飞行器转动引起各位置横向过载的变化Fig.1 nz change at different positions of vehicle caused by rotation

3.2 大飞行包线内的载荷特性

高超声速飞行器所跨空域广,动压变化范围大。本文首先考察Ma=5～20，H=20～50 km范围内,从典型初始状态起始至1 s仿真结束时刻飞行器重心的横向过载。图2给出了是否考虑地球曲率和自转时,Ma对重心横向过载的影响。

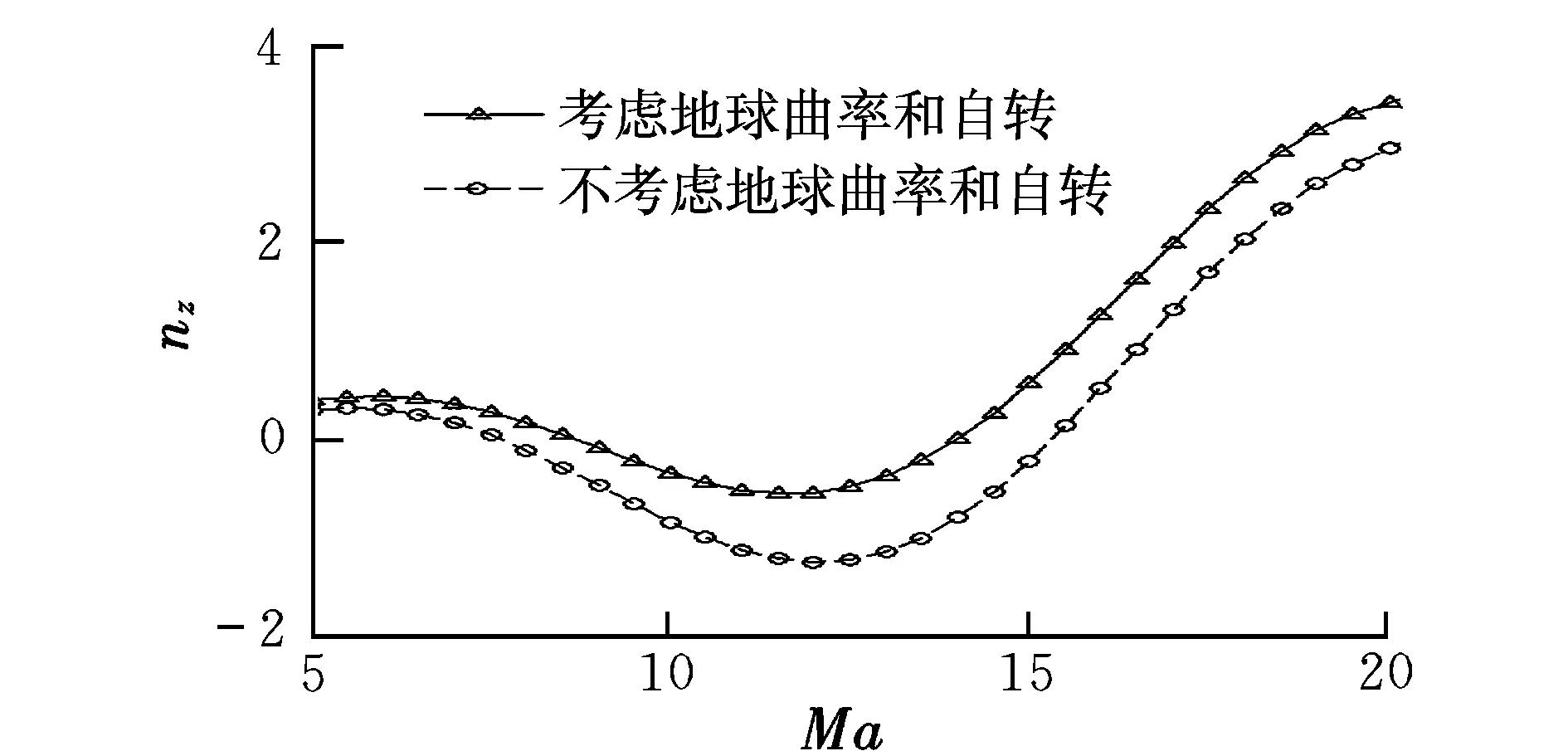
图2 Ma对重心横向过载的影响Fig.2 Effect of Ma on nz of center of mass

与文献[8]给出的结果类似,地球曲率和自转效应对过载的影响在不同Ma处有所变化,总体上来说是不可忽略的。传统分析方法采用平面大地假设,在Ma较高时因为忽略了圆形地球效应和离心力,显然会产生较大误差,故在高Ma载荷分析时需要综合考虑。

图3给出了是否考虑地球曲率和自转时,高度对重心横向过载的影响。模拟结果表明:考虑与不考虑地球曲率和自转因素所产生的横向过载差在30～50 km内基本一致,影响量基本稳定。

图3 高度对重心横向过载的影响Fig.3 Effect of height on nz of center of mass

3.3 质量变化对载荷的影响

在飞行过程中,由于燃料消耗程度不同,再入段飞行器质量不同,重心位置也随之改变[10],影响俯仰力矩,则过载模型中的气动力项发生变化,进而影响飞行器整体过载。在典型初始状态下，质量变化对重心过载变化率的影响如图4所示。

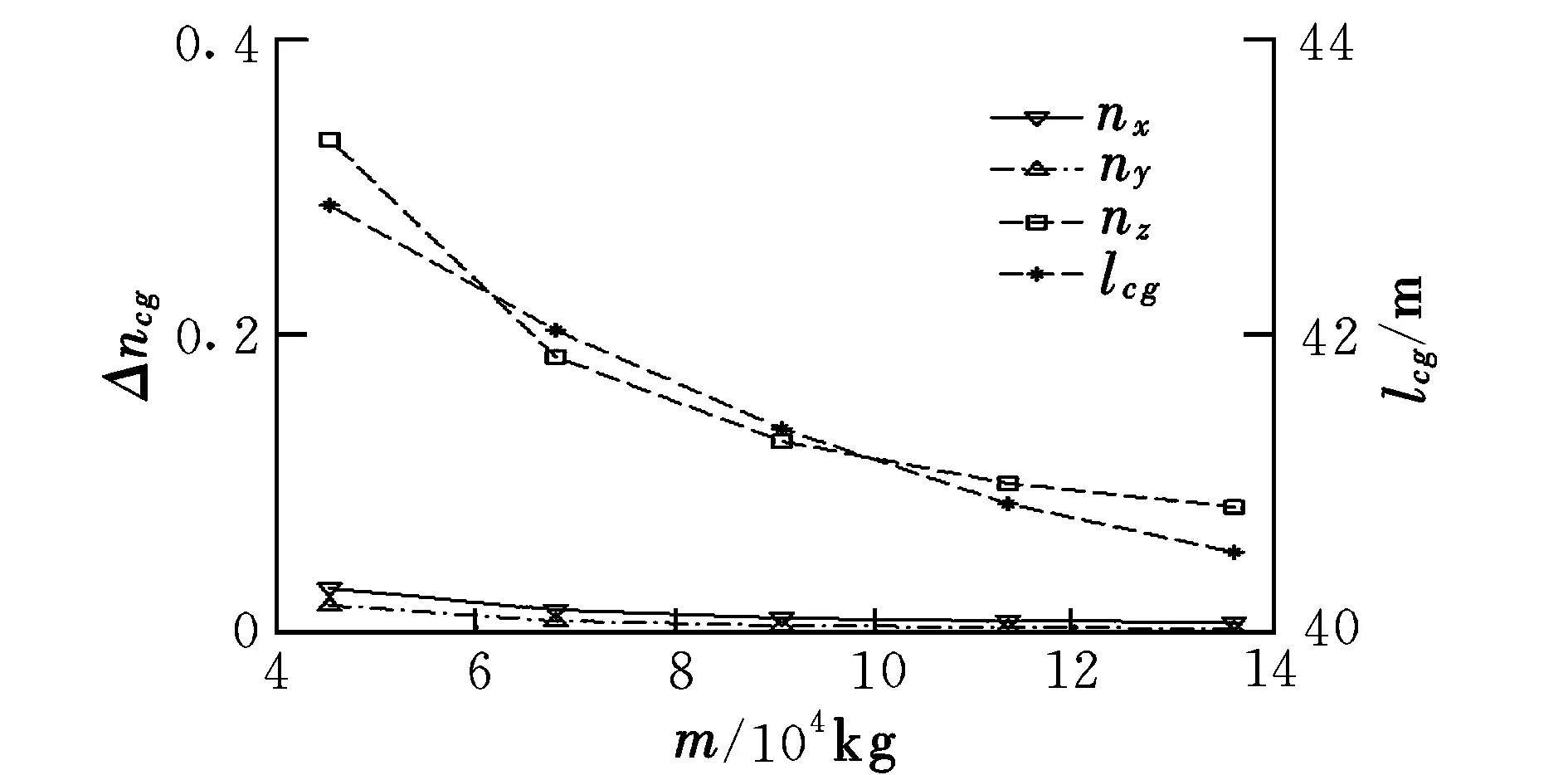
图4 质量变化对重心位置及重心过载变化率的影响Fig.4 Effect of mass change on location and load rate of center of mass

由图4的仿真结果可见,在质量从4×104kg变化到14×104kg的过程中,重心位置从42.8 m减小到40.5 m,产生了明显偏移,这时横向过载对质量的变化比另外两个方向要敏感得多,也大得多。可见在载荷设计中,需要以空载或接近空载状态作为主要分析工况,重点关注横向过载。

3.4 舵面控制与载荷的关系

不考虑反作用控制系统的作用,飞行器控制输入由左右升降舵δer和δel的调节来完成,并令δel=δer=δ。采用半正弦舵偏形式,最大舵偏角20°,通过改变舵偏时间控制舵偏速度,对三向过载进行仿真。三向过载与不同舵偏速度的关系如图5所示。

图5 不同舵偏速度下的三向过载对比Fig.5 Comparison of three-dimensional loads based on different δ duration time

由图5可以看出,舵偏越急,由气动力阶跃产生的过载也越大;横向过载最为敏感,纵向和侧向过载则变化不大。

最大舵偏角直接关系到舵面控制力,并引起过载变化。比较相同初始状态及舵偏形式(半正弦舵偏,舵偏时间2 s),不同最大舵偏角下由气动力阶跃产生的三向过载变化如图6所示。

图6 不同最大舵偏角度下的三向过载对比Fig.6 Comparison of three-dimensional loads based on different maximum δ angle

由图6可以看出,横向过载变化对最大舵偏角最为敏感,而纵向、侧向变化较小,横向过载变化在舵偏角为负最大时取得最大过载值。由此可见,载荷在舵偏角为负、俯仰力矩为正的情况下最敏感,在载荷设计时应重点关注。

4 结束语

本文通过建立考虑地球曲率和自转的高超声速飞行器再入段载荷模型,分析了各因素对载荷特性的影响。结果表明:载荷分析时基于平面大地假设的动力学模型在高超声速飞行时会产生较大误差,这时应采用考虑地球曲率和自转的模型;采用重心过载在机体低速转动时可以用来表征飞行器整体过载;再入飞行器的过载对高度、速度和最大舵偏角敏感性强,飞行器质量变化及相应的重心偏移对飞行器载荷有一定的影响;舵偏速度和最大舵偏角的设置对于载荷控制有着重要意义。

本文未考虑其它飞行阶段的有动力飞行及控制系统的作用,在后续分析中将进一步考虑这些因素对载荷特性的影响。

[1] 国辉宇,谈诚,刘炳坤,等.着陆冲击对人体影响及医学评价问题评述[J].航天医学与医学工程,2002,15(6):455-459.

[2] 伍骥,张凌,高雁旭,等.高性能战斗机飞行对飞行员脊柱影响研究[J].航空军医,2002,30(1):32-35.

[3] 李菁菁,任章,黎科峰,等.高超声速飞行器再入段的动力学建模与仿真[J].系统仿真学报,2009,21(2):534-537.

[4] Snell S A.Nonlinear dynamic-inversion flight control of super maneuverable aircraft[D].Twin Cities,Minnesota:University of Minnesota,1991.

[5] Keshmiri S,Mirmirani M,Colgren R.Six-DOF modeling and simulation of a generic hypersonic vehicle for conceptual design studies[R].AIAA-2004-4805,2004.

[6] Colgren R,Keshmiri S,Mirmirani M.Nolinear ten-degree-of-freedom dynamic model of a generic hypersonic vehicle [J].Journal of Aircraft,2009,46(3):800-813.

[7] Bolender M A,Doman D B.Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle [J].Journal of Spacecraft and Rockets,2007,44(2):374-387.

[8] 鲍文,姚赵辉.综合离心力/气动力的升力体高超声速飞行器纵向运动建模研究[J].宇航学报,2009,30(1):128-133.

[9] 齐乃明,周啓航,秦昌茂.高超声速飞行器六自由度建模及耦合特性分析[J].弹箭与制导学报,2012,32(1):49-52.

[10] Shaughnessy J D,Pinckney S Z,McMinn J D,et al.Hypersonic vehicle simulation model:winged-cone configuration [R].NASA-TM-102610,1990.

[11] 肖业伦.飞行器运动方程[M].北京:航空工业出版社,1984:36-61.

Loadanalysisofnear-spacevehicleinreentrystage

CHEN Hong-yong1,2, CHEN Hai-bo1,2

(1.Department of Modern Mechanics, USTC, Hefei 230027, China;2.Key Laboratory of Mechanical Behavior and Design of Materials, CAS, Hefei 230027, China)

Six DOF dynamic model and its related load model are established for the near-space reentry vehicle which integrate the rolling and curvature effects of the earth and the aerodynamic force of the vehicle. The composition of load and its variation in large flight envelope are studied under open-loop status. Influences of the mass variation as well as elevator control style, action rate and maximum action angle and their coupling characteristics to the load characteristics are investigated. The results show that, the rolling and curvature effects of the earth should not be ignored in the load analysis of near-space reentry vehicle. Load of the vehicle is sensitive to the altitude, the velocity and the maximum elevator angle. Load at the center of gravity could be used to represent the load of the entire vehicle while in the low rotational speed. Mass variation and the related variation of center of gravity have some influence to the load level of the vehicle. Different style, velocity and angle of elevators angular deformation and is important to total load.

near-space vehicle; six DOF dynamic model; load model; elevator control

V414

A

1002-0853(2013)05-0443-04

2013-01-28;

2013-05-14; < class="emphasis_bold">网络出版时间

时间:2013-08-21 16:14

陈红永(1986-)，男，陕西宝鸡人，博士研究生，研究方向为飞行器总体设计及结构分析；陈海波(1968-)，男，福建龙海人，教授，博士生导师，研究方向为计算力学、振动工程、飞行器结构力学。

(编辑：李怡)