波形钢腹板组合箱梁剪滞效应分析

辛立凤 甘前宇 张婉霞

(1.广西工学院鹿山学院土木建筑工程系，广西柳州 545616;2.柳州市建筑设计科学研究院，广西柳州 545006)

波形钢腹板是用波形钢板代替普通箱梁的混凝土腹板，是现代桥梁结构建设中采用体外预应力技术的一种新型钢—混凝土组合结构[1]。

剪力滞是指因箱梁混凝土翼缘板的剪切变形而引起的沿箱梁宽度方向弯曲正应力不均匀分布的现象。

本文利用能量变分法从理论上推导了波形钢腹板组合箱梁在均布载荷作用下的箱梁剪滞效应计算公式，并与有限元分析结果进行比较，验证了理论计算公式的正确性。

1 波形钢腹板组合箱梁剪滞效应的能量变分求解

1.1 基本假定

考虑到一般的表达形式，选取梯形箱梁截面作为研究对象，如图1所示，并引入广义位移函数u(x，y)和w(x)，则箱形梁翼缘板的竖向位移u(x，y)可假设为:

式中:w(x)——箱形梁的竖向挠度位移;

ui(x，y)——箱形梁混凝土翼缘板的竖向位移;

u(x)——箱形梁混凝土翼缘板的竖向位移剪切转角差;

Zd(e)——箱形梁上下混凝土翼缘板的形心到箱形梁中性轴的距离。

1.2 能量变分法基本的方程推导

由最小势能原理可知:

即:

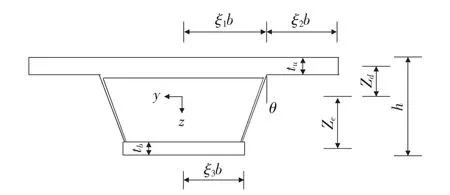
图1 箱梁截面尺寸示意图

a.箱梁弯曲时的载荷势能:

b.当箱梁在纯弯曲条件下的载荷势能:

a.箱梁腹板区域的应变势能[2]:

b.箱梁上翼缘混凝土板的应变能:

c.箱梁下翼缘混凝土板的应变能:

体系的总势能为:

将式(8)变分得到以下微分方程及相应的边界条件:

式(10)表示的是用能量变分法求得的剪滞效应的基本微分方程，式(11)表示的是基本微分方程在边界条件下及连续条件下的表达式。

1.3 能量变分法的基本方程求解

当一简支的箱梁上作用有均布载荷q时，则弯矩和剪力可以表示为:

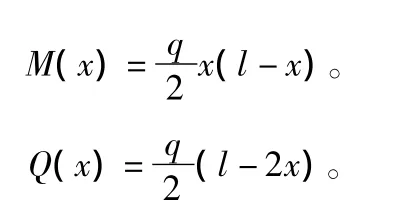
解为:

边界条件为:u'|x=0=0，u'|x=l=0，

附加弯矩为:

曲率为:

应力为:

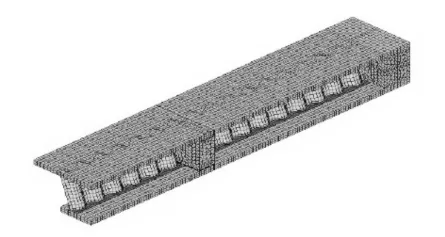
图2 箱形梁的有限元模型图

图3 波形钢腹板箱形梁的纵横断面的单元划分图

2 有限元模型的建立[4]

本文主要以日本新开桥的构造为例，建立单箱单室梯形截面的波形钢腹板简支组合箱梁。该箱梁的总长度为5 m，计算长度4.8 m，波形腹板箱梁的高度为0.36 m。波形钢腹板和钢盖板均用Q235钢，泊松比为0.3，波形钢板的弹性模量为210 GPa，实际测得波形钢板的厚度为0.002 35 m，钢盖板宽度为0.08 m，实际测得的钢盖板的厚度为0.002 73 m。采用ANSYS[5]有限元分析软件，用三维杆单元模拟，混凝土按三维实体单元来模拟。采用三维板壳单元来模拟波形钢腹板，选用三维杆单元来模拟体外索。该箱形梁的有限元模型如图2和图3所示。

3 分析验证

当作用在简支箱梁跨中的均布载荷为8.82 kN/m时，则得到相应于简支梁的顶、底板的应力值，见表1。

表1 箱梁跨中在均布载荷下的纵向应力比较

通过能量变分法计算的结果和有限元的分析结果比较得出:均布载荷作用下的波形钢腹板箱梁，其上、下混凝土翼缘板均会有明显的正剪力滞现象发生，但均布载荷作用下的剪力滞要比集中载荷作用下的剪力滞小。能量变分法和有限元法两者计算出的剪力滞大小和纵向应力相接近。

4 结语

1)波形钢腹板简支箱梁在均布载荷作用下推导出的箱梁顶板和底板的纵向应力及剪力滞微分方程理论计算式中，可以不考虑波形钢板的抗弯变形能的影响。2)通过有限元与能量变分法求解结果的对比，两种方法得出的纵向应力值是比较接近的，说明了本文研究所创立的波形钢板组合箱梁的有限元模型具有一定的可靠性。3)采用本文的能量变分法求解出的波形钢腹板简支组合箱梁的剪力滞理论计算式是偏于安全的。4)由于本文采用的空间有限元分析结果与能量变分法求出的结果相吻合，所以该方法可应用于实际的桥梁工程计算中。

[1] 刘 磊，钱冬生.波纹钢腹板预应力结合梁桥[J].国外公路，1999(2):24-35.

[2] 刘寒冰，刘文会.用变分法分析预应力钢—混凝土组合T梁的剪力滞效应[J].公路交通科技，2004，21(5):65-67.

[3] 彭 鲲.波形钢腹板组合箱梁的剪力滞理论与试验研究[D].长沙:湖南大学，2008.

[4] 潘 颖，邓 宇.基于ANSYS平台计算分析薄壁箱梁的剪力滞效应[J].四川建筑，2007，27(2):153-154.

[5] E.Reissner.Analysis of Shear Lag in Box Beams by the Principle of Minimum Potential Energy[J].Quarterly of Applied Mathematics，1946，14(10):257-269.