超磁致伸缩作动器的结构分析

李 琳 陈亮良 杨 勇

(北京航空航天大学 能源与动力工程学院，北京100191)

超磁致伸缩材料具有应变大、响应速度快、机电耦合系数高、输出力大等特点.近十几年来有关基于超磁致伸缩材料的作动器的研究成为智能结构的一个热点.超磁致伸缩作动器的工作原理是利用材料在交变磁场中可产生交变变形的特性，将材料棒置于一个可控的磁场中，实现对目标的驱动.至目前为止多数研究围绕材料特性以及与材料特性直接相关的输出特性展开，主要涉及材料的预压力特性［1-2］作动器输出的磁滞特性及其建模与控制［1，3-4］等.然而，有关超磁致伸缩作动器内部结构形式对输出特性影响的研究少之又少.而超磁致伸缩作动器的工作原理恰恰是需要通过具体的结构形式来实现.

超磁致伸缩作动器由激励磁场组件、偏置磁场组件、预压组件、超磁致伸缩材料芯棒、连接杆、调节螺母、外壳等部分组成.其中偏置磁场的作用是使作动器具有双向的力和位移输出能力.在这些组件中，直接对作动器的输出产生影响的是材料芯棒、激励磁场组件(涉及激励磁场的实现方式)，偏置磁场组件(涉及偏置磁场的实现方式)以及预压组件(涉及预压力实现方式).激励磁场一般是由通交变电流的线圈的感生磁场实现的，关于线圈的设计理论已经比较成熟了［4-7］;预压组件一般由碟簧实现.因此有可能对作动器的特性产生影响，并需要进一步研究的是偏置磁场组件.

偏置磁场的实现有两类基本形式:一是采用螺线管实现，采用通电螺线管提供偏置磁场的优点是设计简单，而且可以通过控制电流来实现磁场强度的精确控制，但是需要提供持续的恒定电流，因此作动器能耗高、发热量大［5-6］;另一种是采用永磁铁实现［8-10］，永磁铁偏置磁场的优点在于不需要提供恒定电流来保证偏置磁场强度，因此能耗低、发热量小，而且采用高磁能积的铷铁硼材料可以大幅减小作动器的体积;永磁铁的不足在于剩磁强度不可设计、机械加工困难.

除了偏置磁场的结构形式外，外壳材料也会对作动器内部的磁场产生不可忽视的影响.针对这一特点以及目前的研究现状，本文重点研究了永磁铁式偏置磁场的不同结构形式以及作动器外壳材料对作动器的输出性能及作动器轴向刚度的影响，为超磁致伸缩作动器的结构设计提供参考.

1 永磁铁形式及其偏置磁场

典型超磁致伸缩作动器的结构如图1所示.

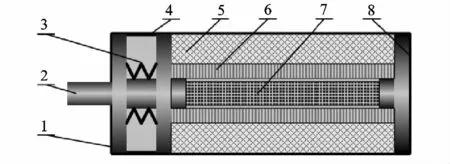
图1 超磁致伸缩作动器结构示意图

根据超磁致伸缩作动器的原理及作动器内部的空间限制，永磁铁的设计形式主要有以下3种［1，4］:内环套式，外环套式和分段式，如图 2 所示.

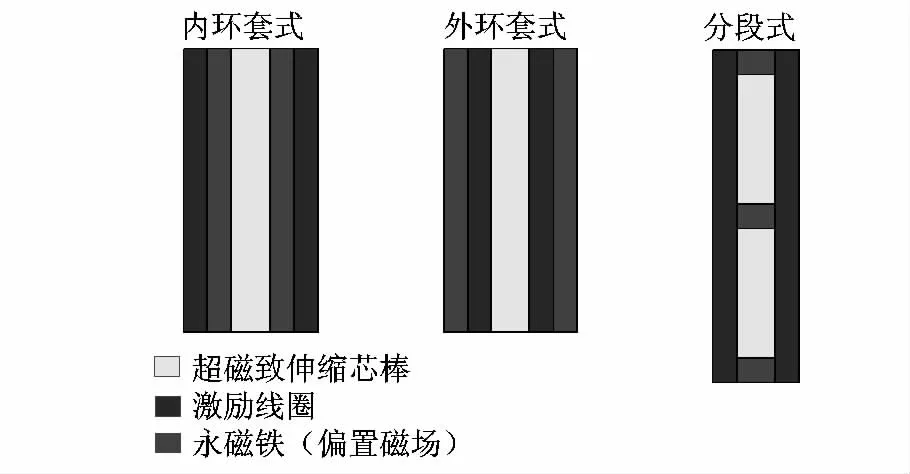
图2 偏置磁场的几种设计形式

不同形式下，永磁铁、磁轭、芯棒及外壳形成的磁回路不同，因此超磁致伸缩芯棒周围的偏置磁场也就不同.在下面的分析中考虑了2种不同的材料作为作动器外壳材料:大磁导率材料——钢，及小磁导率材料——铝.借助有限元软件ANSYS中的磁场分析功能，对作动器建立轴对称的有限元模型并计算，可得到内部结构形式不同的作动器中磁力线的分布及芯棒区域的磁场强度.

1)环套式永磁铁结构及其偏置磁场

环套式永磁铁分为内环套式和外环套式.内环套是指环形磁铁套在超磁致伸缩芯棒外、激励线圈内;外环套是指环形磁铁套在激励线圈外(超磁致伸缩芯棒位于激励线圈内).环形磁铁产生的磁场强度在永磁材料一定时主要由环形磁铁的径向厚度决定.磁场强度分布与作动器外壳相关.对应两种不同磁导率材料外壳，环套式永磁铁的磁力线分布如图3(内环套)和图4(外环套)所示.由图可知，采用大磁导率的钢制外壳时，外壳-磁轭-永磁铁形成闭合的磁回路，没有磁力线通过超磁致伸缩芯棒，这意味着芯棒处的磁场强度近似为零;采用小磁导率的铝制外壳时，虽然有磁力线通过超磁致伸缩芯棒区域，但作动器外部也有大量磁力线通过，这意味着作动器有漏磁现象.

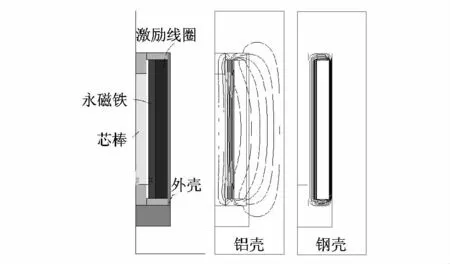
图3 内环套式结构示意图及磁力线分布

磁力线的分布表明，钢制外壳作动器不漏磁，但芯棒处的磁场强度很小;铝制外壳作动器中芯棒处的磁场强度可通过设计满足要求，但作动器漏磁现象严重，这使作动器周围形成较大的磁场，有可能会对作动器周围的仪器设备产生影响.

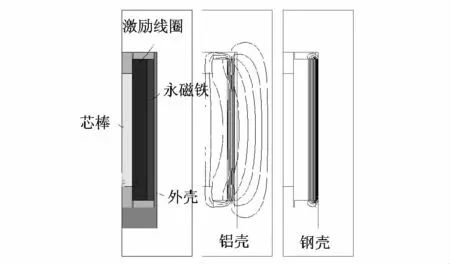
图4 外环套式结构示意图及磁力线分布

图5给出了铝制外壳作动器中采用内环套式永磁铁实现偏置磁场时芯棒中的磁场强度沿芯棒长度分布的曲线(外环套永磁铁的分布曲线与之类似).钢制外壳情况中，超磁致伸缩芯棒区域的磁场强度几乎为零，因此未在图中绘出.分析选取了3个不同位置(芯棒不同半径位置)对比分析.该分布表明，芯棒中不同半径位置偏置磁场沿芯棒长度方向分布相同(表明磁场强度沿芯棒径向均匀分布);沿芯棒长度方向的分布与理想均匀分布有差异，算例中环形磁铁长度为100 mm，磁场强度的最大值约为最小值的1.2倍左右(钢壳、铝壳情况相同).

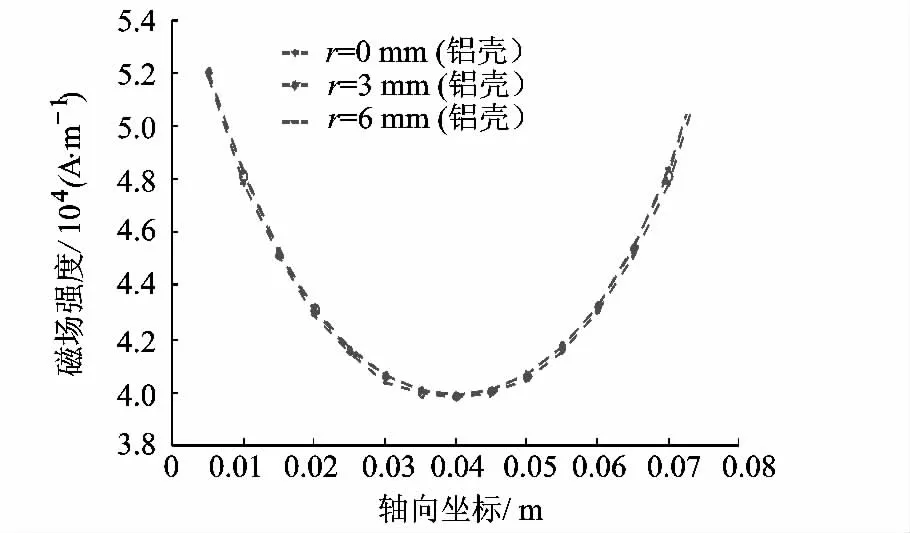
图5 内环套式永磁铁的磁场强度轴向分布(铝壳)

2)分段式永磁铁结构及其偏置磁场

分段式结构中永磁铁由数个圆片状磁铁组成，超磁致伸缩芯棒也被分为若干段;圆片状磁铁与芯棒相间叠置.分段式永磁铁产生的磁场强度在永磁材料一定时，主要取决于圆片的厚度.磁场分布与作动器外壳材料相关.图6给出2种不同外壳材料的分段式永磁铁结构的磁力线分布.从图中可见，不论外壳材料如何都有大量的磁通分布在芯棒区域;但是大磁导率外壳基本没有漏磁现象，而小磁导率外壳有明显的漏磁现象.

图7给出对应两种材料外壳情况芯棒(被分为两段)中磁场强度沿芯棒长度的分布曲线，每条曲线对应不同半径r处的分布.由图7可见，①采用分段式永磁结构时，小磁导率的铝制外壳作动器的芯棒区域磁场强度小于大磁导率的钢制外壳作动器的芯棒区域磁场强度.②不论外壳材料的磁导率如何，芯棒区域的磁场强度沿半径基本是均匀分布的;③芯棒区域的磁场强度沿芯棒长度方向的分布不均匀;对于两段40 mm的芯棒的情况，芯棒中最大磁场强度为最小磁场强度的2倍左右;不论外壳材料的磁导率如何，芯棒中磁场强度沿芯棒长度方向的分布具有相似的曲线形式.

图6 分段式结构示意图及磁通分布图

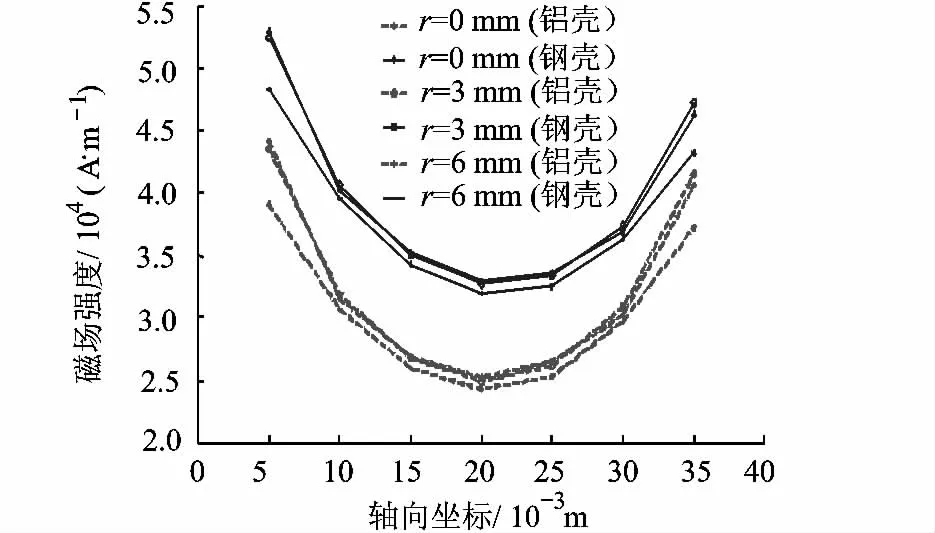
图7 分段式磁场强度的轴向分布

综上所述，采用分段式永磁铁偏置磁场时，用大磁导率材料的外壳能提高芯棒中的磁场强度而不改变磁场分布规律，并且没有漏磁现象.

2 永磁铁对作动器输出位移的影响

第1小节的分析表明，不论何种形式的永磁铁在芯棒周围产生的磁场强度都不为恒值，其沿径向的分布尚可近似认为均匀，沿芯棒长度的分布则为一条曲线，中间部分的磁场强度最小，两端的磁场强度最大;实际偏置磁场与理论偏置磁场(磁场强度为一恒值)的差异将对作动器的输出产生直接的影响.图8给出对应两种典型实际偏置磁场的定长芯棒的行程输出与对应理想偏置磁场的定长芯棒行程输出的比较(设激励磁场相同).两种典型实际偏置磁场的最小值分别大于和小于理想的偏置磁场(为一恒值)，它们都使芯棒的实际行程输出低于按均匀偏置磁场设计的芯棒行程输出，特别是当实际偏置磁场有低于理想的设计均值的部分，且这一区域大于1/2的芯棒长度时，行程输出曲线甚至还会出现倍频现象.

为了获得这一输出损失与偏置磁场结构设计的关系，下面分别分析作动器的正位移输出损失Δsup和负位移输出损失Δsdown(见图8).

图8 作动器输出曲线图(不同偏置磁场)

设计作动器时，为了使作动器在伸、缩方向具有对称的输出，通常将偏置磁场的强度Hp及激励磁场HA的幅值设计成最大驱动磁场强度Hmax的一半，则作动器中的磁场为

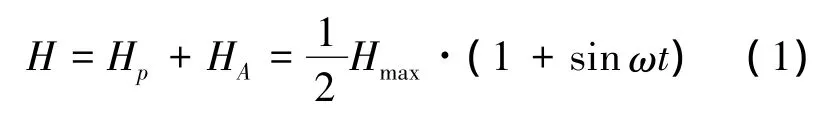
该磁场中、长度为l的芯棒能产生的伸缩量s可以由式(2)得到(λ为超磁致伸缩芯棒的应变):

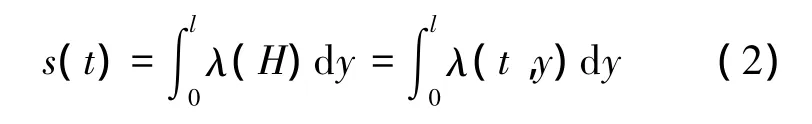
偏置磁场的另外一个作用是使材料芯棒在其特性曲线(λ-H)的线性段工作.因此，可以近似取

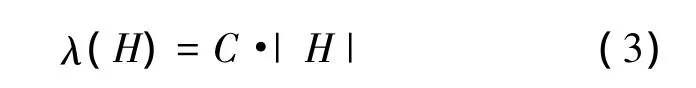
式中C为常系数.将式(1)代入式(3)可得

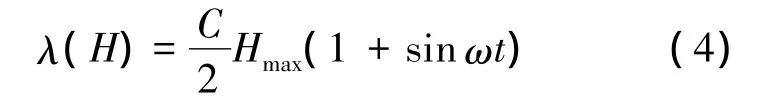
再将式(4)代入式(2)得

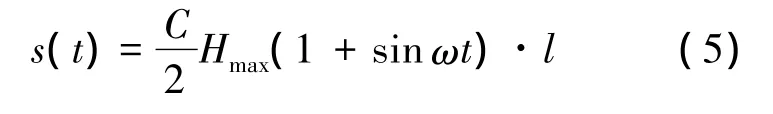
可知，芯棒的最大输出位移为λmaxl=CHmaxl.得到这一结论的前提是偏置磁场为理想的均匀磁场.当偏置磁场沿芯棒长度变化时，作动器的输出小于理想值.设y1与y2为实际偏置磁场沿芯棒轴向的分布曲线与理想的均匀分布直线的交点，［y1，y2］即偏置磁场强度低于理想值Hmax/2的区间;作动器的正位移输出损失Δsup和负位移输出损失Δsdown的表达式如下:

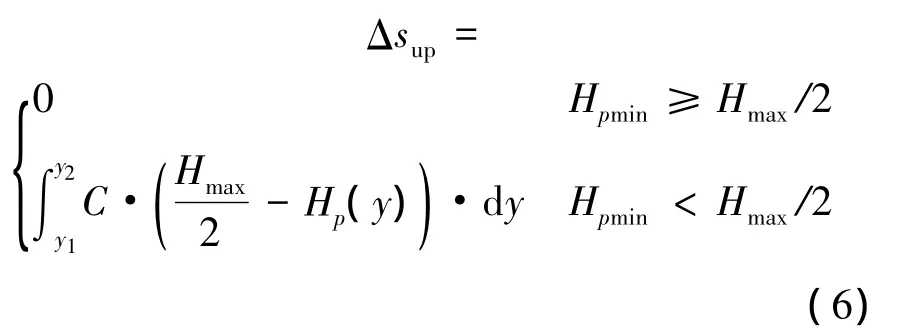
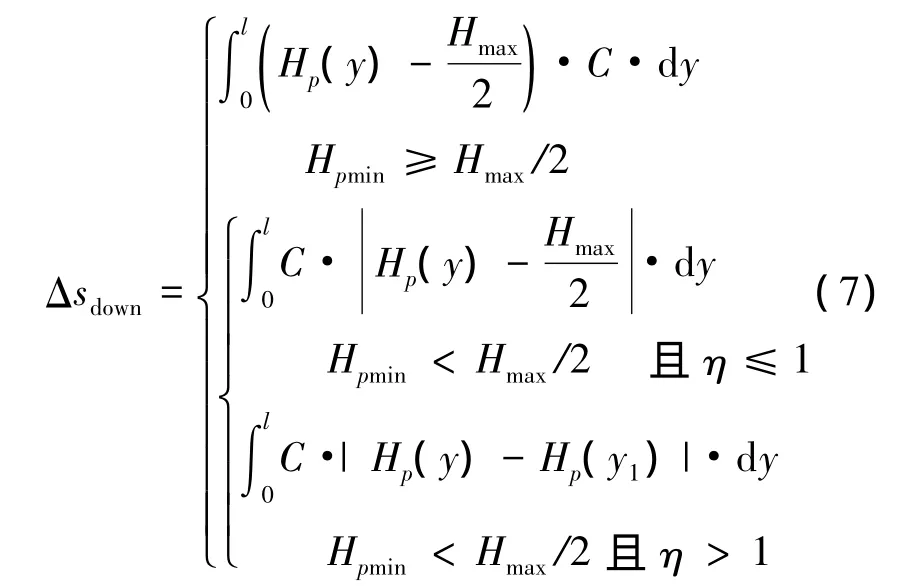
式中，η =(y2-y1)/0.5L.当区间［y1，y2］大于芯棒长度一半时，意味着大部分芯棒处的驱动磁场强度在交变时有可能为负，这是产生倍频现象的根本原因.总的行程损失为式(6)、式(7)之和:

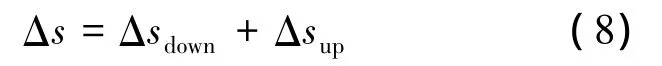
将实际偏置磁场的分布曲线用顶点(最小值Hpmin)位于芯棒中点的抛物线函数来近似时，即

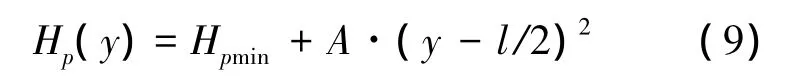
式中，A=4·(Hpmax-Hpmin)/l2;Hpmin≤Hmax/2.对应不同的Hpmin和Hpmax的偏置磁场分布曲线如图9所示，其中 1#，2#，3#曲线是 Hpmin＜Hmax/2 的情况(1#和 2#的 η＞1，3#的 η＜1);4#和 5#曲线是 Hpmin＞Hmax/2的情况.

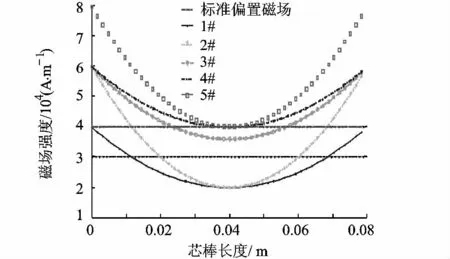
图9 沿芯棒长度方向呈抛物线分布的磁场强度

表1给出对应这几种偏置磁场分布的芯棒输出行程及其损失率.(芯棒长度为80 mm，最大磁致伸缩系数为1000 μm/m.)

表1 偏置磁场的分布对芯棒输出行程的影响

表1表明，实际偏置磁场的不均匀分布产生的行程损失是很可观的.偏置磁场分布的越均匀，行程输出的损失越小，如对应3#，4#分布的输出.从这一观点出发，偏置磁场的设计应采用磁场分布相对均匀的环套式永磁铁.然而，第1节的分析表明，环套式永磁铁会在作动器周围产生较大的磁场，需慎重采用.

采用分段式永磁铁时，鉴于分段式永磁铁产生的不均匀磁场特性，在设计偏置磁场时，必须考虑由此产生的行程输出损失，同时在可能的情况下增加分段数，可以改善磁场分布的不均匀度.此外，保证最小磁场强度(芯棒中段的磁场强度)接近或等于设计的理想磁场强度也可减小行程输出的损失.

3 永磁铁对作动器轴向刚度的影响

在智能结构系统的设计中，除了作动器的输出特性外，作动器自身的刚度也是一个必须高度关注的特性，它直接影响智能结构系统的动力学性能.超磁致伸缩作动器的刚度一般是指轴向(位移输出方向)的刚度.由超磁致伸缩作动器的内部结构可知，其轴向刚度主要取决于芯棒的刚度和碟簧的刚度.对于普通材料，等截面棒的轴向刚度为EA/L，E为材料的弹性模量，A为棒的横截面积，L为棒的长度.然而，对于超磁致伸缩材料，其弹性模量E与材料的应力环境σ和磁场环境H相关.因此超磁致伸缩作动器中实现偏置磁场的结构会从以下两方面影响作动器的刚度:

1)永磁铁的结构形式

图10为超磁致伸缩作动器的结构刚度分析模型，其轴向刚度为芯棒的轴向刚度Ka与预压碟簧的刚度Kd的并联刚度，即

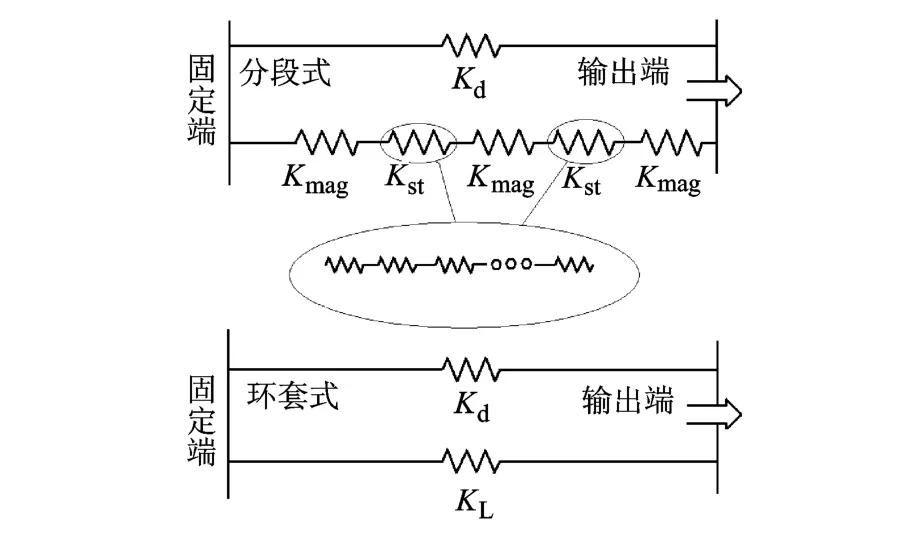
图10 超磁致伸缩作动器的结构刚度分析模型

环套式永磁铁，芯棒为一等截面圆柱体，在等应力和等磁场强度条件下，其轴向刚度为

分段式中材料芯棒被分为若干段，段与段之间用永磁圆片间隔;图10中给出的是芯棒分段数为2的示意.如此形成的驱动芯棒的轴向刚度为

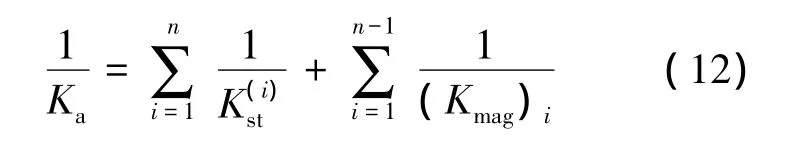
2)永磁铁为芯棒提供的磁场环境

超磁致伸缩材料的E与σ和H有关.郑晓静等［11］给出了超磁致伸缩材料应力应变及磁场之间的关系，如式(13)、式(14)所示.本节的分析中以此为基础，获得材料E与σ和H之间的关系:

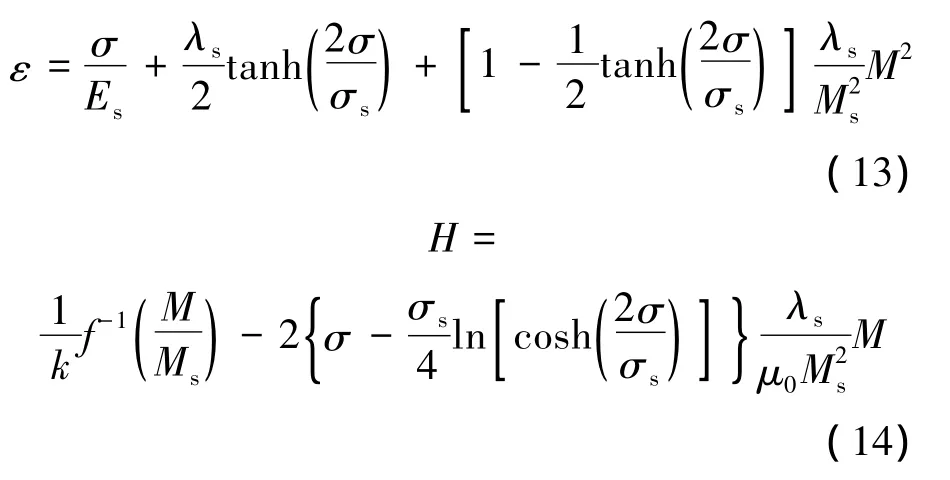
式中，He表示有效磁场强度.模型中的5个材料参数为:松弛因子k、饱和弹性模量Es、饱和应力σs、饱和磁致伸缩应变λs和饱和磁化强度Ms.基于上述方程，对于特定芯棒材料的参数，运用数值迭代方法可以计算出芯棒材料在不同磁场下的应力应变关系，再利用杨氏模量的定义，可得对应于给定参数的芯棒弹性模量E(σ，H).对应设计的预压力值，可得弹性模量随磁场强度的变化曲线E(H).在研究磁场强度的影响时，可将该曲线用一个拟合的多项式来近似，如图11所示.

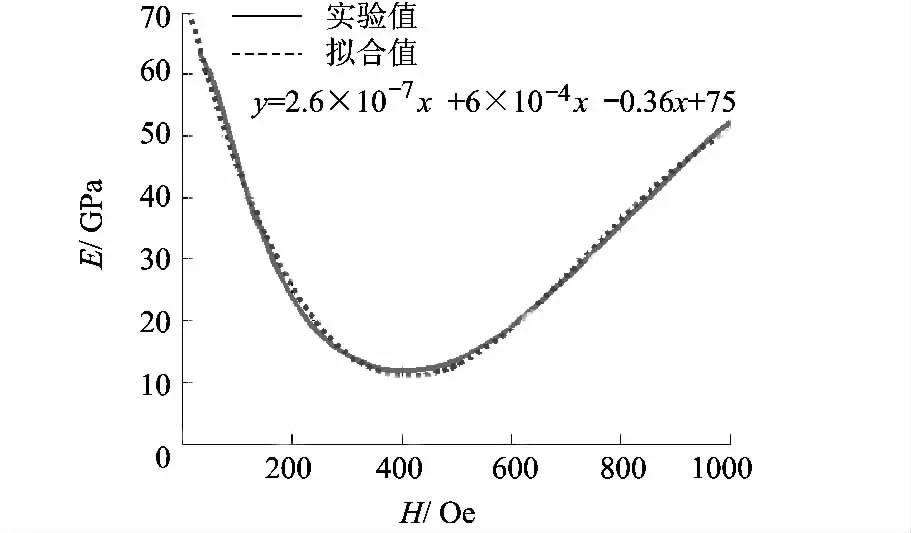
图11 10 MPa时E(H)曲线及其拟合方程

如前述，永磁铁所产生的磁场沿芯棒长度的分布为一曲线，这意味着每一段芯棒所处的磁场强度不同，因而芯棒的杨氏模量也不相同，从而影响了作动器的轴向刚度.根据图11，材料弹性模量有极小值;当理想均匀磁场位于极值点右侧时，增加磁场强度，材料的弹性模量随之增大，因此芯棒的刚度也会增大;反之则减小.

表2给出对应图9磁场分布、基于图11的E-H曲线计算的作动器刚度，理想的偏置磁场强度为Hmax/2=500 Oe(大于弹性模量极值对应的磁场强度;芯棒长度为80 mm，分段式中按两段考虑).计算中考虑了E随H的变化，该结果既反映了永磁铁结构形式对作动器刚度的影响，也反映了偏置磁场的分布对作动器刚度的影响.作动器轴向刚度变化通过δK=(K-Kideal)/Kideal来表示.结果表明，作动器的刚度与理想均匀偏置磁场设计的刚度有较大差异.偏置磁场的整体强度(以偏置磁场最小值为标志)增大，则作动器刚度增大.磁场分布均匀与否的影响是通过对应芯棒区域的磁场强度来体现的.以3#，4#和5#磁场分布(图9)为例，4#曲线的均匀度优于3#和5#，对应这3种磁场分布的作动器的刚度则是依次增大，原因是3#，4#，5#的磁场强度是依次增加的.

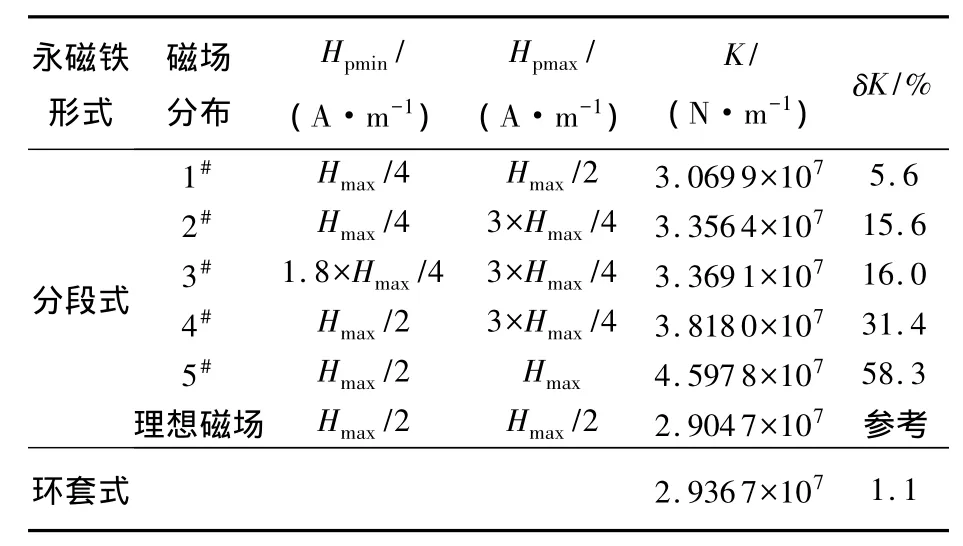
表2 不同偏置磁场对作动器轴向刚度的影响

4 结论

本文针对超磁致伸缩作动器结构设计中的关键问题——实现偏置磁场的结构形式展开研究，所得结论归纳如下:①由环套式永磁铁产生的磁场虽然比较均匀，但是存在严重漏磁现象，在实际应用中有可能产生意想不到的问题，因此不建议采用;②采用分段式永磁铁可避免漏磁现象;③分段式永磁铁产生的磁场与设计值(理想均匀磁场)有较大差异，对作动器的输出和刚度均具有不可忽视的影响，在设计中必须考虑;④分段式永磁铁产生的偏置磁场对作动器刚度的影响与偏置磁场强度的整体水平正相关或负相关，取决于设计预压力与设计偏置磁场强度(理想均匀)下材料弹性模量与其极值的关系.

References)

［1］贾振元，郭东明.超磁致伸缩材料微位移执行器原理与应用［M］.北京:科学出版社，2008 Jia Zhenyuan，Guo Dongming.Theory and application of giant magnetostrictive microdisplacement actuator［M］.Beijing:Science Press，2008(in Chinese)

［2］ Yoshio Y，Hiroshi E，Jun S.Application of giant magnetostrictive materials to positioning actuators［C］//IEEE/ASME International Conference on Advanced Intelligent Mechatronics.Atlanta，USA:［s.n.］，1999

［3］ Ma Y，Mao J.Modeling and control for giant magnetostrictive actuators with stress-dependent hysteresis［C］//International Conference on Automation and logistics.Qingdao，China:［s.n.］，2008

［4］ Grunwald A，Olabi A G.Design of a magnetostrictive(MS)actuator［J］.Sensors and Actuators A:Physical，2008，144(1):161-175

［5］夏春林，丁凡，路甬祥.超磁致伸缩材料驱动器实验研究［J］.电工技术学报，1999，14(4):14-17 Xia Chunlin，Ding Fan，Lu Yongxiang.Experimental study on giant magnetostrictive transducer［J］.Transactions of China Electrotechnical Society，1999，14(4):14-17(in Chinese)

［6］马志新，周志平.基于超磁致伸缩材料微位移驱动器的原理及实验研究［J］.现代机械，2009，2:19-21 Ma Zhixin，Zhou Zhiping.Design and experimental analysis of a micro displacement actuator based on giant magnetostrictive material［J］.Modern Machinery，2009，2:19-21(in Chinese)

［7］ Zhang H，Zhang T，Jiang C.Magnetostrictive actuators with large displacement and fast response［J］.Smart Materials and Structures，2012，21(5):055014-7

［8］张磊，束立红，何琳，等.磁致伸缩作动器的设计与性能分析［J］.海军工程大学学报，2006，18(4):75-79 Zhang Lei，Su Lihong，He Lin，et al.Design and characteristic analysis of giant magnetostrictive actuator［J］.Journal of Naval University of Engineering，2006，18(4):75-79(in Chinese)

［9］徐峰，张虎，蒋成保.超磁致伸缩材料作动器的研制及特性分析［J］.航空学报，2002，23(6):552-555 Xu Feng，Zhang Hu，Jiang Chengbao.Designing and perfromance research of giant magnetostrictive actuator［J］.Acta Aeronautica Et Astronautica Sinica，2002，23(6):552-555(in Chinese)

［10］ Karunanidhi S，Singaperumal M.Design analysis and simulation of magnetostrictive actuator and its application to high dynamic servo valve ［J］.Sensors and Actuators A:Physical，2010，157(2):185-197

［11］ Zheng X，Liu X.A nonlinear constitutive model for terfenol-D rods［J］.Journal of Applied Physics，2005，97(5):053901-8