双压电驱动微泵泵膜的ANSYS 仿真和结构优化分析

邓 凯，陈可娟

（华南理工大学 机械与汽车工程学院，广东 广州 510640）

1 引言

微泵是微机电系统（MEMS）中重要的执行器件[1]，在医学应用、电子元件冷却、环境监测等领域发挥着重要的作用[2]。微泵的驱动方式有很多，主要包括压电驱动、静电驱动、电磁驱动、热驱动、光驱动、气动力驱动和形状记忆合金驱动等。其中压电驱动具有能耗小、响应时间短、可靠性高、结构简单等特点而在微泵中得到广泛的应用[3-6]。压电驱动微泵是利用晶体的压电特性驱动泵膜振动来工作的[7]，因此泵膜的结构设计是压电驱动微泵设计的重点。在传统单压电层泵膜的基础上，提出了一种新型的双压电驱动泵膜结构。为了提高微泵的工作效率，对双压电泵膜进行了小挠度弯曲形变理论分析，同时运用ANSYS 有限元分析软件对泵膜进行模拟仿真，对仿真数据进行分析，得出泵膜参数对泵膜形变位移和一阶谐振频率的影响，并利用正交试验方法对泵膜结构进行了优化。

2 泵膜的结构和小挠度弯曲形变理论

2.1 泵膜结构

对于传统的压电驱动微泵，泵膜上层为压电陶瓷PZT 薄膜，下层为单晶Si薄膜，在PZT 薄膜的上下面各有一层金属薄膜电极。新型泵膜的结构，如图1 所示。半径为R0，泵膜上、下层为压电层，中间为基层，在压电层上下面各有一层金属薄膜电极，各层是粘结在一起的。薄膜电极层材料是Ag，厚度为H2，在分析泵膜力学特性时可以忽略电极厚度的影响；压电层材料是PZT-5A，厚度为H1；基层材料为Si，厚度为H0。

2.2 压电复合泵膜小挠度弯曲形变理论

在泵膜的上、下电极上施加一定幅值的电压，由于压电陶瓷材料的逆压电效应，会使整个泵膜产生弯曲变形。如果施加的电压是具有谐振频率的交变电压，泵膜会产生谐振。为了研究泵膜的弯曲变形，利用柱坐标来表示泵膜的结构尺度，rθ 平面位于泵膜的中性面上，Z 轴是对称轴，基层顶面、上压电层顶面在柱坐标中的坐标分别是Z1、Z2。

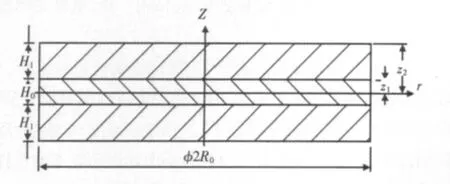
图1 柱坐标下的泵膜结构Fig.1 Pump Membrane Structure at Cylindrical Coordinates

由于新型泵膜在电压驱动下的弯曲变形是轴对称问题，所有的应力和应变分量都只是r的函数，不随θ 变化。根据薄板小挠度弯曲理论的假设则有：εz=0，γzr=0，γzθ=0。

在泵膜电极层上加载电压，泵膜压电层会有电场，由于假设εz=0，所以泵膜弯曲形变的物理方程为[8]：

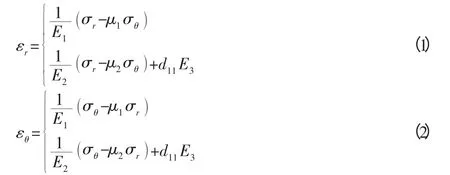
式中：E1、E2—泵膜基层Si、电极层PZT-5A的弹性模量；μ1、μ2—Si、PZT-5A的泊松比；E3—加在压电层上的电场强度；d11—压电层纵向压电效应的压电常数。

根据上述分析，建立泵膜弹性曲面的微分方程为[9]：

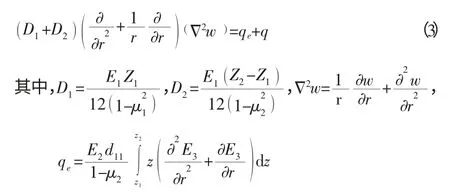
3 泵膜的有限元分析

3.1 有限元建模和网格划分

图2 泵膜网格划分图Fig.2 Grid Partition Figure of Pump Membrane

在ANSYS 平台上对双压电复合泵膜进行有限元仿真分析，主要模拟压电复合泵膜在不同驱动电压和不同结构参数下的弯曲变形和挠度分布情况。利用ANSYS 建立的有限元分析模型，如图2所示。在建模时电极层、压电层和基层之间采用Glue 命令粘合在一起，模型属于压电耦合分析，所以选用ANSYS/Multiphysics 模块。泵膜压电层材料是PZT-5A，选用的分析单元六面体耦合实体单元SOLID5；基层和电极层的材料分别是Ag 和Si，选用的分析单元是六面体实体单元SOLID45。模型网格划分时，采用扫掠网格划分，单元形状为六面体单元网格，将驱动电压作为施加载荷，边界条件是周边固支[10-11]。

3.2 泵膜的静态和模态分析

3.2.1 泵膜的静态分析

利用ANSYS 对压电泵膜进行电压激励静态分析，在一定电压驱动下，泵膜发生弯曲形变，由于泵膜周边固支，因此泵膜中心处形变位移最大，整个泵膜变形后成抛物曲面分布，如图3 所示。在驱动电压为50V，泵膜半径R0为10mm，电极层厚度H0为5μm，压电层厚度H1为50μm，基层厚度H2为10μm的条件下对泵膜进行静态分析。

图3 泵膜静压形变位移图Fig.3 Static Deformation Displacement of Pump Membrane

3.2.2 泵膜的模态分析

固有频率和振型是微泵泵膜设计中的重要参数，可通过模态分析获得。在泵膜半径R0为10mm，电极层厚度H0为5μm，压电层厚度H1为50μm，基层厚度H2为10μm的条件下对泵膜进行模态分析。在分析仿真中，提取了膜片的三阶谐振频率，仿真得出泵膜的一阶谐振频率为2254Hz，二阶和三阶谐振频率都为4693Hz。泵膜的一阶、二阶、三阶模态振型图，如图4 所示。由图4 可以看出，泵膜一阶模态振型的振动形式成抛物线振动，二阶和三阶模态振型的振动形式都被分成了两个小区域，而微泵泵膜的工作振型应该与一阶模态振型相似。因此，驱动电压的频率应该小于一阶谐振频率，才能保证微泵有效的工作。

图4 泵膜的模态振型图Fig.4 Modal Shape Figure of Pump Membrane

3.2.3 泵膜半径的影响

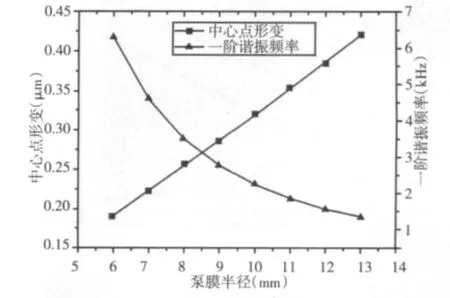
图5 半径对泵膜中心点形变和频率的影响Fig.5 Influence of Radius to Pump Membrane Deformation and Frequency

半径对泵膜中心点形变和频率的影响，如图5 所示。由图5可以看出，泵膜中心点形变位移与泵膜半径成正比例关系。泵膜半径增大，泵膜各点的形变位移也随之增大，泵腔可以产生的体积变化越大，微泵的输出效率就越高，但是泵膜半径受到微泵整体结构的限制，在满足微泵结构要求的前提下，可尽量取较大的泵膜半径。泵膜的一阶谐振频率则与半径成反比例关系，随着泵膜半径的增大，它的一阶谐振频率逐渐减小，为了保证微泵的高效工作，驱动电压的极值频率也要随之减小。因此在选择泵膜半径时除了考虑半径对泵膜形变位移的影响，还要综合考虑半径对一阶谐振频率的影响。

3.2.4 泵膜厚度的影响

压电体、硅基层和金属电极层厚度对膜片驱动都有影响作用。由于在实际应用中，膜片电极层很薄，在对膜片进行小挠度形变理论分析时可以忽略。为了提高仿真的精度，在应用ANSYS 软件对膜片进行仿真时，将电极层的影响也考虑在其中。模拟的结果，如图6 所示。由图6（a）可以看出，电极层厚度越小，微泵泵膜在电压驱动下的形变位移就越大，但是随着电极层厚度的减小，膜片的一阶谐振频率近似正比例关系下降。同理由图6（b）可以看出，压电层厚度对膜片驱动的影响与电极层类似；硅基层对膜片形变的影响很小，对膜片一阶谐振频率的影响与电极层相似，这与文献报道不同，说明双压电层泵膜与单压电层泵膜有着不同的性质。另外，减小电极层、压电层和基层厚度受到了加工工艺和泵膜强度要求的限制，因此在选择电极层、压电层和基层厚度时，应该综合考虑，合理减小泵膜厚度。

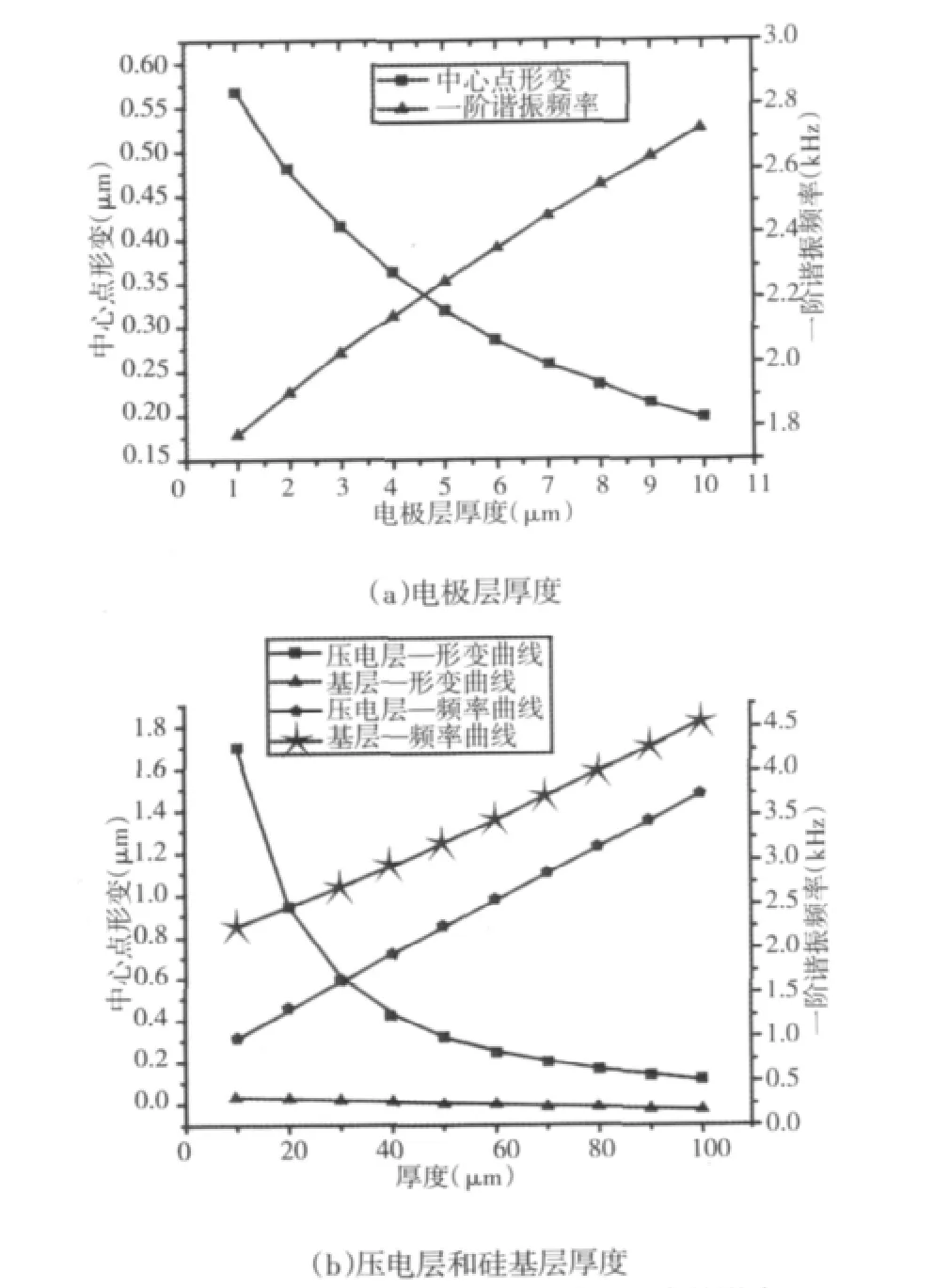
图6 厚度对压电泵膜中心点形变和频率的影响Fig.6 Influence of Layer Thickness to Pump Membrane Deformation and Frequency

4 结论

（1）对新型泵膜的静压驱动分析发现，驱动电压、泵膜半径、基层厚度、压电层厚度、电极层厚度都会影响泵膜中心点的形变位移，从而影响微泵的工作效率，其中压电层厚度对泵膜中心点形变影响最大，其次依次是驱动电压、泵膜半径、电极层厚度、基层厚度。

（2）泵膜的模态分析发现，为了保证微泵的正常工作，要使泵膜的振型保持一阶模态振型，因此驱动电压频率要小于泵膜的一阶谐振频率。泵膜半径、基层厚度、压电层厚度、电极层厚度都会影响泵膜的一阶谐振频率，从而影响驱动电压频率的选择，其中泵膜半径对泵膜一阶谐振频率影响最大，其次依次是压电层厚度、电极层厚度、基层厚度。

（3）为了提高微泵的工作效率，在设计泵膜参数时，既要考虑它们对泵膜形变的影响，要考虑它们对泵膜一阶谐振频率的影响，还要考虑泵膜的加工工艺条件、泵膜强度、微泵的整体结构等问题。

［1］赵安，种银保.基于MEMS的微泵研究现状与进展［J］.医疗卫生装备，2010，31（2）：46－49.（Zhao An，Zhong Yin－bao.Investigation progress review of micro－pump based on MEMS［J］.Chinese Medical Equipment Journal，2010，31（2）：46－49.）

［2］胡志翔，邹俊，谢海波.基于Mat lab的微型无阀泵系统仿真分析［J］.机床与液压，2003（3）：24－25.（Hu Zhi－xiang，Zou Jun，Xie Haibo，et.Flow simulation and analysis of the micro valve－less pump［J］.Machine Tool and Hydraulics，2003（3）：24－25.）

［3］OLSSON A，STEMME G，STEMME E.Diffuser－element design investigation for valve－less pumps［J］.Sensors and Actuators，1996（57）：137－143.

［4］OLSSON A，STEMME G，STEMME E.A valve－less planar fluid pump with two pump chambers［J］.Sensors and Actuators，1995，46－47：549－556.

［5］陈荣，王文.静电驱动柔性振膜型微泵的动力学分析［J］.工程热物理学报，2010，31（2）：197－200.（CHEN Rong，WANG Wen.Theoretical analysis on micro electrostatic diaphragm pump［J］.Journal of Engineering Thermo physics，2010，31（2）：197－200）

［6］朱玉田，许溱，陈茂林，等.基于光致弯曲材料的微泵设计研究［J］.功能材料，2011，42（11）：1943－1946.（Zhu Yu－tian，XU Qin，Chen Mao－lin，et.Design and research of micro－pump based on photo－induced bending material［J］.Functional Materials，2011，42（11）：1943－1946.）

［7］Junwu K，Zhigang Y，Taijiang P，et al.Design and test of a high performance piezoelectric micro－pump for drug delivery ［J］.Sens.Actuators A：Phys，2005，121（1）：156－161.

［8］王立文，高殿荣，杨林杰.压电驱动微泵泵膜振动有限元分析［J］.机械工程学报，2006，42（4）：230－234.（Wang Li－wen，Gao Dian－rong，Yang Lin－jie.Finite element analysis of the membrane oscillation of the piezoelectric micro－pump［J］.Chinese Journal of Mechanical Engineering，2006，42（4）：230－234.）

［9］刘鸿文主编.板壳理论［M］.杭州：浙江大学出版社，1987：118－125.（Liu Hong－wen.Shell Theory［M］.Hangzhou：Zhejiang University Press，1987，118－125.）

［10］刑静忠，王永岚，陈晓霞.ANSYS 分析实例与工程应用［M］.北京：机械工业出版社，2004：223－225.（Xing Jing－zhong，Wang Yong－gang，Chen Xiao－xia.ANSYS analysis examples and engineering application［M］.Beijing：Mechanical Industry Press，2004：223－225.）