重型车辆轮胎原地转向阻力矩研究

张小江，丁宏刚，朱亚夫，赵建国，陈建凯

（1.吉林大学 机械科学与工程学院，吉林 长春 130022；2.徐工集团 徐州重型机械有限公司，江苏 徐州 221004）

1 引言

轮胎转向阻力矩直接关系到车辆机械转向系统、液压助力转向系统的匹配设计，而轮胎在原地转向时所产生的阻力矩是最大的。因此有必要对轮胎原地转向阻力距进行分析。轮胎原地转向阻力矩大小主要由路面摩擦系数、轮胎气压、车轮转角和轮胎载荷等决定[1]，同时与车胎转速相关。轮胎在原地转向过程中，转向阻力矩比较复杂，轮胎原地转向时，轮胎在绕主销转动的过程中，轮胎与地面的运动边滚边滑。以原地转向时的阻力矩作为计算转矩能保证在不利条件下进行转向[2]。目前根据原地转向的试验结果总结出来的经验公式有3 个[3]：半经验公式、雷索夫推荐公式、塔布莱克推荐公式。另外参考文献[4－5]通过试验发现车辆原地静止转向时，其转向阻力矩和车轮转角具有一定的关系，但是参考文献前提供的轮胎转向阻力矩公式给出的只是轮胎最大的原地转向阻力矩，没有给出转向阻力矩和车轮转角的变化的一般规律，也没有给出转向阻力矩和车轮转速的关系。轮胎与地面的摩擦阻力矩一般为行驶转向时的（2～3）倍。为了得到重载轮胎原地转向阻力矩和车轮转角的变化情况，有必要对重载轮胎的原地转向阻力矩进行深入分析。文献[6]采用Lugre 模型对回转关节处的摩擦建立了如下模型：Mf=rFNμ（z，z˙，v），文献[7]将Lugre 模型用于电液位置伺服系统的摩擦力矩中。文献[8]利用Lugre 模型补偿了直流电机系统并给出了试验结果。

2 原地转向阻力距分析

轮胎在原地转向过程中，转向阻力矩比较复杂，轮胎原地转向时，轮胎在绕主销转动的过程中，轮胎与地面的运动边滚边滑，导致轮胎在原地转向过程中和地面作用产生的印迹近似为扇形。由于复杂的轮胎受力变形特性、轮胎和地面之间的协调大变形滑动接触以及复杂的地面土壤力学特性等方面的原因，使得车辆轮胎与地面的相互作用分析比较困难。由于轮胎和地面接触状况的复杂性，建立一个能够全面描述轮胎地面接触特性的模型是不太可能的，即便是建立起来，也会由于过于复杂而没有实际应用价值[9]。为了分析轮胎原地转向阻力矩，将机械系统中的LuGre 摩擦模型应用于轮胎与地面的摩擦分析中。LuGre 模型是Dahl 模型的扩展，同时采纳了鬃毛模型的思想，LuGre 模型是基于鬃毛的平均变形来建模。将LuGre 模型引入轮胎原地转向阻力矩中，为了考虑轮胎转动角速度和轮胎原地转向阻力矩的关系，模型中考虑了黏性摩擦项fωω，Stribeck 效应用g（ω）表示为：

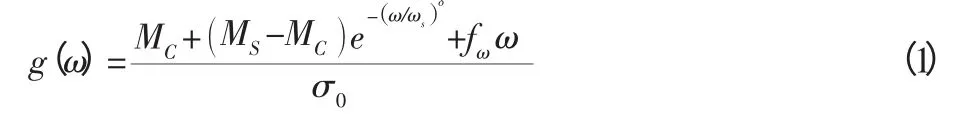
式中：MC—库仑摩擦力矩；MS—最大静摩擦力矩；ω—轮胎旋转角速度；σ0—鬃毛的刚度；σ1—微观阻尼系数；σ2—黏性摩擦系数；ωS—Stribeck 速度；ωS，δ—经验常数。

鬃毛的平均变形量用状态变量z 表示，建模为：

轮胎的原地转向阻力矩公式为：

由公式（1）、（2）和（3）可以看出，利用Lugre 模型得到的轮胎原地转向阻力矩特性由σ0、σ1、σ2、fw和ω 决定。σ0、σ1、σ2、fw和ω 一般需要通过试验的方法来确定。

3 轮胎垂直载荷对转向阻力矩的影响

根据原地转向的试验结果总结出来的半经验计算公式指出轮胎原地转向阻力矩和轮胎垂直载荷成的关系式为：

式中：Mr—原地转向阻力矩（N·mm）；Fz—转向轴负荷（N）；P—轮胎气压（MPa）；μ—轮胎与地面摩擦系数。

半经验公式说明了轮胎原地转向阻力矩和轮胎垂直载荷、轮胎气压和地面摩擦系数的关系，为了获得轮胎与地面摩擦产生的库仑摩擦力矩和最大摩擦力矩，假设此两者和轮胎垂直载荷、轮胎气压和地面摩擦系数也符合式（4）的关系，即：

式中：μC—库仑摩擦系数；μS—最大静摩擦力系数；

4 转向阻力矩的试验测试

为了验证轮胎模型的正确性，针对轮胎原地转向阻力矩进行专项测试研究，为轮胎模型提供试验数据。试验用到的仪器有：转角传感器、压力传感器、全隔离信号变送器、数据采集分析仪、笔记本电脑、数据线等。

试验主要针对单个轮胎测试，因此，将第一轴转向直拉杆和转向梯形横拉杆拆除，使车轮在转向油缸的作用力下独立转动。

轮胎转向阻力矩是通过转向油缸输出力及其力臂换算处理后得到的。转向油缸输出力通过测得油缸大小腔压力换算得到。根据车桥结构参数，算出转向油缸推力在不同的车轮转角情况下的力臂。

为了分析轮胎垂直载荷对轮胎原地转向阻力矩的影响，对某轮胎进行了不同载荷下的转向阻力矩试验，试验测得轮胎垂直载荷30000N、40000N、50000N、60000N、70000N 三种不同载荷下的轮胎原地转向阻力矩，如图1 所示。针对轮胎原地转向阻力矩进行专项测试研究，为轮胎模型提供试验数据。

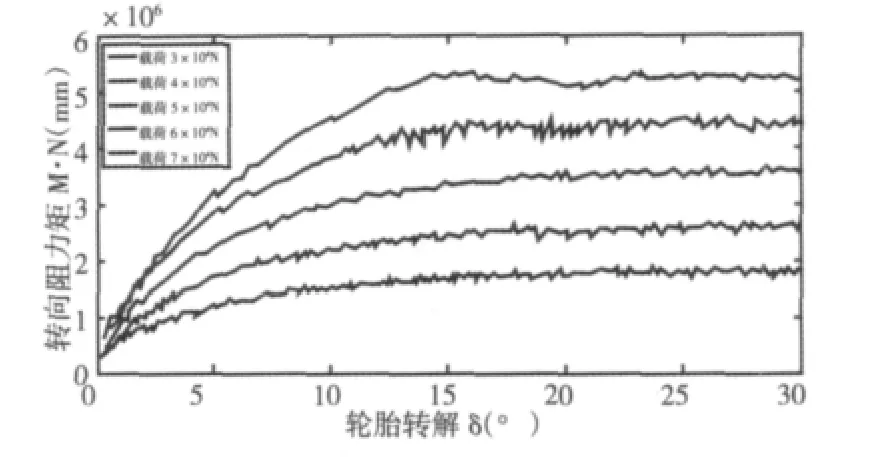
图1 不同垂直载荷下轮胎原地转向阻力矩试验数据Fig.1 Experimental Data of Static Steering Resisting Moment Curve under Different Vertical Load

5 计算结果和比较

选择轮胎载荷为50kN 进行仿真对比，该工况下轮胎转角的时间历程曲线，如图2 所示。仿真过程中，Lugre 模型主要参数，如表1 所示。

表1 主要技术参数Tab.1 Main Parameters

经过仿真后，仿真结果时间历程曲线和试验数据的对比曲线，如图3 所示。从仿真图像可以看出，Lugre 模型和试验数据时间历程曲线有比较好的跟随性。

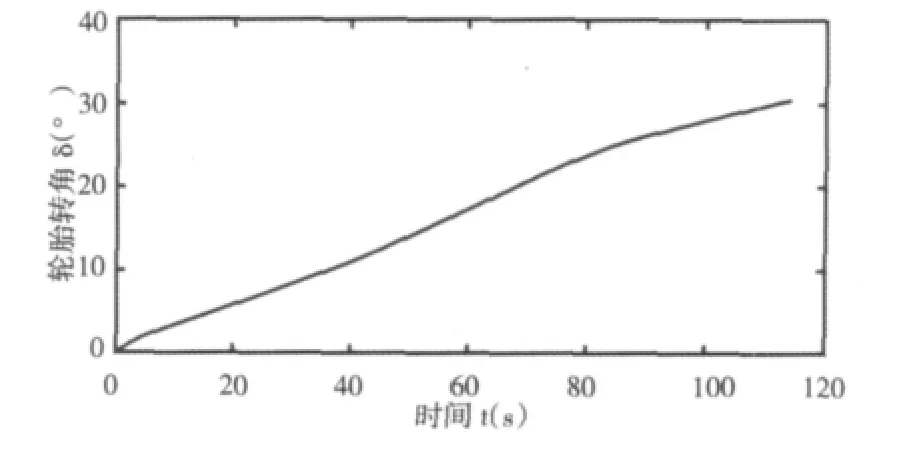
图2 轮胎转角时间历程曲线Fig.2 Time History Curve of Tire Steering Angle

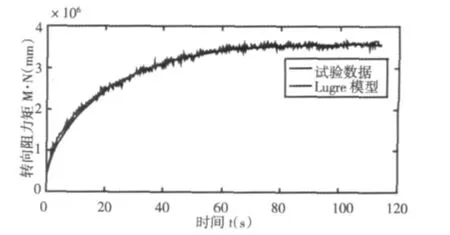
图3 Lugre 模型和试验数据对比Fig.3 Comparison between Lugre Model and Experimental Data

运用Lugre 模型对转向阻力矩进行仿真，其仿真结果，如图4 所示。

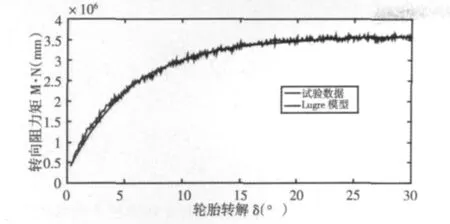
图4 轮胎原地转向阻力矩对比Fig.4 Comparison of Static Steering Resisting Momen

从图4 可以看出，Lugre 模型得到的转向阻力矩仿真数值和试验测试得到的结果是一致的。由此可以说明采用Lugre 模型来模拟轮胎原地转向工况更为合理，能反应出转向阻力矩和轮胎转动角速度的关系。但Lugre 模型物理意义理解困难，不容易被工程设计人员吸收，实际运用会存在一定的困难。

从仿真图像也可看出：原地转向阻力矩随着车轮的转角的变化表现出一定的非线性，随着轮胎转角的增加，原地转向阻力矩增加的速率逐渐变缓，最后趋于某一定值。传统经验公式只是表示出了原地转向阻力矩的最大值，没有表示出轮胎转角和原地转向阻力矩的关系，这和工程实际有出入。采用Lugre 模型很好的表示出了轮胎转角和原地转向阻力矩的关系式，并用试验得到了很好的验证，因而采用Lugre 模型来表达轮胎的原地转向阻力矩是可行的和可信的，同时为液压助力转向系统设计提供参考依据。

6 总结

对车轮原地转向过程中的转向阻力矩进行了试验研究，从试验结果可知：车轮原地转向阻力矩并非一个定值，而且随着车轮的增加而增加，最终趋于一定值；将Lugre 模型应用于车轮的原地转向过程中，其仿真结果都和试验数据较为一致。

［1］黄朝胜，李骏.轮胎特性对载重汽车性能的影响［J］.轮胎工业，2007，27（1）：3－10.（Huang Chao－sheng，Li Jun.Influence of tire characteristics on truck performance［J］.Tire Industry，2007，27（1）：3－10.）

［2］林慕益，张福生.车辆底盘构造与设计［M］.北京：冶金工业出版社，2006.（Lin Mu－yi，Zhang Fu－sheng.Vehicle Chassis Structure and Design［M］.Beijing：Metallurgical Industry Press，2006.）

［3］王彦会.多轴转向汽车转向特性研究［D］.长春：吉林大学，2005.（Wang Yan－hui.The steering characteristic reseach on a multi－steering axle’s vehicle［D］.Changchun：Jilin University，2005.）

［4］黄朝胜，吴碧磊，应国增.载货汽车转向系统分析［J］.汽车技术，2005（5）：19－23.（Huang Chao－sheng，Wu Bi－lei，Ying Guo－zeng.Analysis of truck steering system［J］.Automobile Technology，2005（5）：19－23.）

［5］黄朝胜.重型载货汽车底盘性能设计参数控制研究［D］.长春：吉林大学，2005.（Huang Chao－sheng.A study on design parameters control of performance of heavy duty truck chassis［D］.Changchun：JiLin University，2005.）

［6］Nitsche R，Gaul L.Smart friction driven systems［J］.Smart Mater Struct，2005（14）：231－236.

［7］吴盛林，刘春芳.基于Lugre 模型的电液伺服系统摩擦力矩动态补偿［J］.机床与液压，2003（2）：67－69.（Wu Sheng－lin，Liu Chun－fang.Friction dynamic compensation for electric－hydraulic servo systems based on lugre friction model［J］.Machine Tool＆Hydraulics，2002（2）：67－69.）

［8］C.Canudas de Wit，P.Lischinsky.Adaptive friction compensation with partially known dynamic friction model［J］.Int.J.Adaptivecontrol and Signal Processing，1997（11）：65－80.

［9］任茂文，张晓阳，王戬.车辆地面力学研究现状与展望［J］.机械制造与自动化，2007，（4）：1－6.（Ren Mao－wen，Zhang Xiao－yang，Wang Jian.A review of development and current study of vehicle－terramechanics［J］.Machine Building ＆Automation，2007（4）：1－6.）