对“平行四边形”教学的评析

哈尔滨市龙涤新世纪学校 赵守文

“1·3·3·4”教学模式是我校自2012年开展的一项课题实验，“平行四边形”是杨俊杰老师按照“1·3·3·4”教学模式所进行的教学设计和教学实录.为此作如下认识与反思.

一、全面把握新数学课程标准的内涵及其实质

新数学课程标准分总目标和学段目标。总目标分为知识技能、数学思考、问题解决和情感态度“四维目标”.在这一总目标下，学生要具备“四个基本”数学素养（基础知识、基本技能、基本思想、基本活动经验）；“两个能力”（发现和提出问题的能力、分析和解决问题的能力）；一个价值（了解数学价值、具有初步的创新意识和科学态度）.数学目标包括结果目标和过程目标.结果目标用“了解”“理解”“把握”“运用”等行为动词表述，过程性目标用“经历”“体验”“探索”等行为动词表述.

对平行四边形的知识目标、过程目标的把握，必须在备课准备上下功夫.重组加工教学内容，对教学素材的再创造.

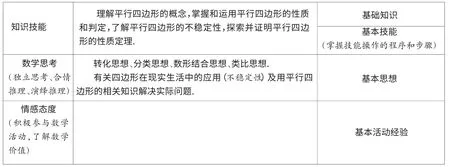
上面的图表具体体现了“平行四边形”这节课的“四维目标”和“四个素养”之间的统一关系，实现理解知识、掌握技能、感悟思想、积累经验的目标.

二、准确定位、构建整体教学内容

数学知识的教学，一定要注重知识的理解，体会数学间的关联，处理好局部知识与整体知识间的关系，注重知识的结构和体系.

从下面的“平行四边形拓展、延伸、关联结构图”不难看出这点.区域1是“平行四边形”这节课的知识结构，而区域1外的内容则是凸显了其与初中数学相关知识的关联.同时渗透了相应的数学思想，及处理数学问题的有关方法，形成了一个完整的知识系统.

平行四边形拓展、延伸、关联结构图

此结构图体现以知识技能为核心和载体，整体考虑知识间的关联，揭示相应的数学方法和数学思想，恰到好处的习题配备，找准知识点，连接知识链，构成知识网，构造整体知识结构，局部的知识结构与全局知识结构的有机结合.

三、科学设计互动开放的教学过程

教学不是教师单纯的知识介绍，也不是学生的单纯模仿、练习和记忆.而应让学生在互动的过程中，感悟知识的形成和运用.新知识学习要展现“知识背景——知识形成——内部关联”活动的过程；知识应用要体现“问题情境——建立模型——求解验证”的过程.概括起来应为：

确定合理教学目标——准确定位教学内容——创设启发性教学情境——精心设计探究问题——自主合作的探究过程——精辟的教师归纳概括.

在这里，着重点是问题设计，问题设计包括：

关于获取信息能力——设计阅读分析的问题；

关于探究能力——设计探索规律的问题；

关于解决问题能力——设计具有实际背景的问题；

关于创造能力——设计开放性问题.

在整体教学过程中要抓好：定位知识点——选择切入点——点拨引领点——训练层次点——落实检测点——师生亲和点——整合知识点.过程也要体现两种推理，相辅相成.

四、精彩彰显教学风格和特色

教学风格体现在多渠道和多元化的特点：

关于多渠道展示：

民主性教学环境；

整体性教学内容；

多渠道探究过程；

多样性教学手段；

层次性思维训练.

关于多元化特点：

全员与局部的统一；

预设与生成的统一；

合情推理与演绎性推理的统一；

知识技能与方法应用的统一；

教学内容与信息技术的统一.

1.全体与个体的统一.

新课程标准中基本理念开宗明义，数学教学要面向全体学生，适应学生个性发展，使得人人能获得良好的数学教育，不同的人在数学上得到不同的发展.这体现了数学教学要面向全体学生，更要面向个体需求.对学习有困难的学生，要及时关注与帮助，鼓励进步，增强学习信心；对学有余力的学生，要给他们足够的材料，配备相应的训练，提供思维的空间，发展其特长和能力.

2.“预设”与“生成”的统一.

教师的教学方案是教师对教学过程的预设，教学方案的形成依赖教师对教材的理解、钻研和再创造.根据学生情况选择贴切的教学素材和教学流程.

实施教学方案，是把“预设”转化为实际的教学活动，在这个转化过程中，师生互动往往会“生成”一些新的教学资源.如新情况、新问题、新思路、新方法、新结果，这些都是动态生成的.这些新资源要及时把握，因势利导，适时调整预案，收到好的效果，这是一笔宝贵的财富.

3.合情推理与演绎性推理的统一.

推理贯穿于数学教学始终，推理能力的形成需要一个长期渐进的过程.合理性推理：通过观察、画图、操作、展示、归纳、类比等活动，发现规律、猜想结论.

平移、旋转、对称、重叠、画图多媒体演示多种手段认知平行四边形的概念和性质.

演绎性推理：通过从合理性推理得到的启发，凭借经验和直观、归纳和类比，从已有的事实和确定的规律，按照逻辑推理方法，证明计算，推断结果.

通过严格推理，从理论上用多种方法证明平行四边形的性质定理：对边平行、对角相等、对角线互相平分.把证明作为探索活动的自然延续和必要发展.要充分理解证明基本方法的掌握和证明过程的体验.

4.知识技能与方法应用的统一.

数学过程体现数学知识的形成过程和反映数学知识的应用过程.

学习掌握知识技能是必要的，但最重要的是对知识技能的应用.应用到实际生活中去，应用到解决具体的数学问题中.综合运用数学知识解决简单的实际问题，增强应用意识，提高实践能力.数学应用尽可能贴近学生现实、生活现实和数学现实，使学生感受到数学的价值和趣味.

5.课程内容和信息技术的整合.

信息技术可以创设模拟多种与数学内容适应的情境，能为学生数学探究提供重要工具.其真正的价值在于实现原有教学手段难以达到甚至达不到的效果.实现模拟演示与学生能够操作的实践活动有机结合；演示与学生的直观想象、规律探究活动结合；实现课程内容与现代信息技术整合.提供丰富多彩的教学环境，提供有利的教学工具，提供探索复杂问题、多角度理解数学的机会，丰富学生的数学视野.