葡萄酒评分优化模型

吕孙忠

(温州大学数学与信息科学学院，浙江 温州 325035)

引言

葡萄酒因其特殊的营养价值和较好的保健效果，越来越受到广大消费者的欢迎。在此形势下，葡萄酒认证和质量评价得到关注，而它的质量鉴别主要靠感官分析和理化指标分析［1］的方法来确定。而感官分析常常通过聘请一批有资质的评酒员进行品评，每个评酒员在对葡萄酒进行品尝后对其分类指标打分，然后求和得到其总分，从而确定葡萄酒的质量。但由于评分受品酒员的主观个人的感受和思维影响，难以用精确的数字来描述，因此造成看起来十分精确的分数却不能精确地说明葡萄酒质量的优劣状态。分组评分法是目前主流的一种评分法之一，对于每组给出的评分，需要检验是否存在显著性差异，并且选择合适的评分组，作为葡萄酒最终得分的主要依据。但评分是精确到个位的，评酒员也说不清楚个位是如何得出的。如果让评酒员们给出一个定性的评价，如“优秀，良好，合格”，这比给出一个分值容易的多，也可以更加客观地表述葡萄酒的质量。

方差分析是英国统计学家R.A.Fisher于20世纪20年代提出的一种统计方法，有着非常广泛的应用，肯德尔和谐系数是检验测量结果信度的方法之一，逆序数可以解释评酒员的评价方向差异。本文利用方差分析去评定两组及两组以上的评分数据中是否存在显著性差异，并利用方差、肯德尔和谐系数和逆序数这三个指标来选择较为合理评分组，同时使用模糊综合评价将各位评酒员的评分转换为定量的分数，使成绩的评定更加客观、合理。

1 方差分析

当对样本进行方差分析检验时，样本应该满足三个基本假设，所有的样本均来自正态分布总体，这些总体具有相同的方差，且所有观测相互独立。所以，在进行方差分析前，需要对样本进行正态性检验和方差齐性检验。方差分析属于参数检验，常见的有单因素方差分析和多因素方差分析。但是，当原始数据不满足正态性和方差齐性假定时，参数检验可能会给出错误报告，此时应采用基础秩的非参数检验，如Kurskal-Wallis［2］非参数检验。

1.1 Kurskal－Wallis模型求解

非参数方差分析:检验的假设是:k个独立的样本来自于相同的总体，当假设成立，并且样本容量足够大时，检验统计量近似服从自由度为k的分布，即检验统计量H近似服从自由度k-1的χ2分布，即

其中，k为样本数，nj(j=1，2，…k)为第j个样本的样本容量，，Ri为第j个样本的秩和。对于给定的显著水平，当H的观测值大于或等于(k-1)时，拒绝原假设，表示k个独立样本来自于不同的总体，或者说k个处理间有显著差异，此时应进一步作多重比较，分析两个处理间有显著的差异。

1.2 逆序数

在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。如2431中，21，43，41，31是逆序，逆序数是4，为偶排列。逆序数在评价性问题中有着广泛的应用［3］，同时它也是检验测量结果信度的方法之一。将一组中每位评酒员所给的平均分按从高到低排序，则一类酒在该组所有评委所打的分从高到低的排名中的秩形成一个排列，计算该排列的逆序数，这个指标有效的分析了每位评酒员的评价方向的差异，逆序数越小，则评分越公平合理。

1.3 肯德尔和谐系数

肯德尔和谐系数［4］是检验测量结果信度的方法之一，根据它可以检验品酒员评分的可信度。

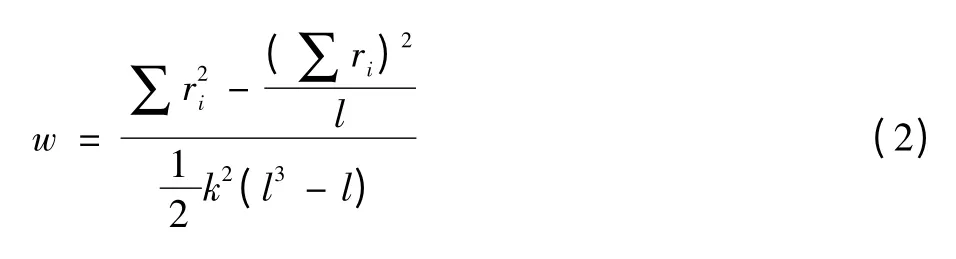
其中，w为肯德尔和谐系数，k为评酒员人数，l是葡萄酒样本数，ri是葡萄酒样品i的评分和。

2 模糊综合评价体系

2.1 层次分析法生成权向量

葡萄酒的感观评价中，可以由外观分析、香气分析和口感分析等n个因素共同决定，记做C1，C2，…，Cn，aij表示Ci和Cj对评分的影响之比，根据层次分析法［5］，可形成对比矩阵，aij的取值见表1。

表1 尺度aij的含义

当形成对比矩阵时，需要进行一致性检验，λ是n阶矩阵的特征根，一致性指标。RI的取值见表2。若一致性指标通过，则可以认为对比矩阵A是基本一致的，如果未通过检验，则需要重新构造对比矩阵。

表2 RI值

求矩阵A的特征分解向量，对特征向量进行归一化处理，则可到评价指标的权向量W=(w1，w2…wn)。

2.2 模糊矩阵

建立模糊综合评价体系［6-9］，将每个评价指标Ci的评定分数划分为m个等级，等级i对应分值ci(i=1，2，…m)，每个评委的分数按照最近邻法，划分等级，即一个评委对Ci的评分为x，重新赋值x，若，当i=j时成立，则x=cj。记对评价指标Ci给出等级ci(i=1，2，…m)的人数占总人数的比例为bij，其中1≤i≤n，1≤j≤m，得到模糊评价矩阵B:

把模糊评价矩阵B和层次分析法得到的权重向量W进行合成，得到模糊子向量D:

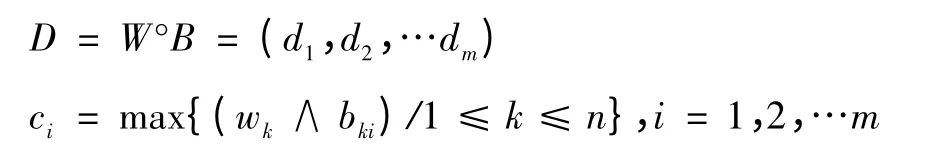
在对向量进行归一化处理，得到模糊评价子向量β=(β1，β2，…βm)，其中

总分S为模糊子向量和其对应级别分值的积。S=β·c=(β1·c1+β2·c2+…βm·cm)，则S为最终评价所得的分数。

3 应用实例

2012年全国大学生数学建模竞赛A题，以白葡萄酒的为例，本实验利用MATLAB［10］求解。首先，需要建立模型说明两组评酒员的数据是否存在差异。在得到两组评价结果存在显著性差异时，还需要进一步说明哪一组的分析结果更加可信。一种简单而直观的做法是考察对每组数据的偏离程度，但这种做法的数据利用率较低，而且大量信息容易被这一指标掩盖，所以，需要引进更加理性化的指标，在利用原始数据的基础之上，进行进一步分析。最后再利用较为合理的数据，得到葡萄酒的最终评分。

3.1 方差分析

由于品酒员的打分，常常带有一定的主观因素，而在他们的感觉评价中，有不同的准确度和精确度，因此，需要建立合适的模型，去分析两组分析结果是否存在显著性差异。调用lillietest函数对白葡萄酒得分数据进行正态分布检验，两组数据的p值为0.3297和0.3308都大于0.05，说明白酒的两组得分的在显著性水平0.05下接受原假设，两组的得分都服从正态分布，其概率分布如图1和图2所示。再对整体数据进行方差齐性检验，调用vartestn函数分别检验两组评委的打分，得到白葡萄酒的p值0.0123＜0.05，拒绝假设，则白葡萄酒两组得分不服从方差相同的正态分布。

图1 第一组白酒概率分布图

图2 第二组白酒概率分布图

通过数据分析，可以得知两组品酒员的数据不服从方差相同的正太分布，所以引入了非参数方差分析。调用kruskalwallis函数白葡萄酒的p=0.0438，小于0.05，所以有显著的差异。调用multcompare函数进行多重比较，得出白葡萄酒的矩阵为:

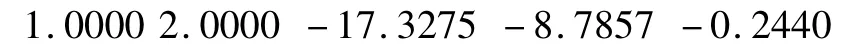
从矩阵可以看出每个矩阵第三和第五个区间不含0，说明两组存在显著差异，其交互式图形如图3所示，可以更加的清晰看出每种酒的评价存在显著差异。

图3 交互式图

3.2 逆序数和肯德尔和谐系数

样本方差反映了样品所得总分与最终结果的平均偏离程度，也反应了评酒员评价尺度的差异，先计算样本方差。再将一组中每位评酒员所给的平均分按从高到低排序，则一种样品酒在该组所有评委所打的分从高到低的排名中的秩形成一个排列，计算该排列的逆序数，同时，再根据k=10，l=28计算肯德尔和谐系数。当选样本数大于7时，检验统计量为χ2计量，χ2=k*(l-1)*wi，i=1，2。则χ2服从自由度为l的χ2分布，若χ2＞χ(l)α，则有100*(1-α)%的准确率可以断定10个品酒员的评分存在相关。各项指标的计算结果见表3。

根据表3，从方差角度和逆序数角度分析，第二组的偏离程度较小且评委们评价方向也较为一致，从肯德尔和谐系数来看，第二组存在相关的概率大于第一组。综合三个指标，则第二组品酒员的评价结果更为可信。

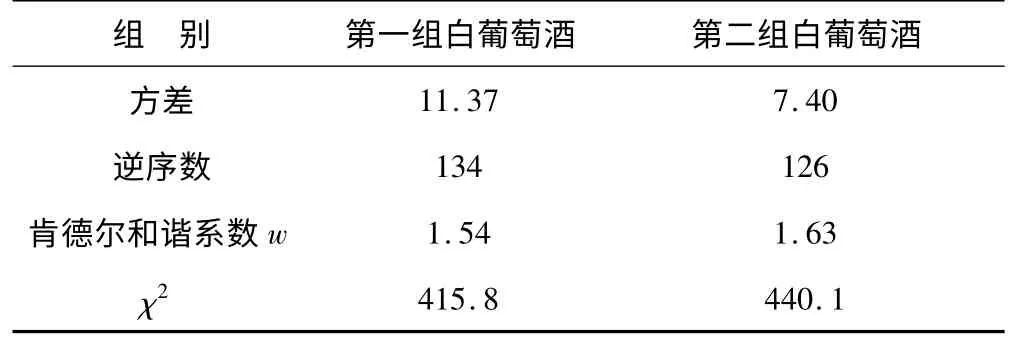
表3 两组标值

3.3 建立评价体系

在葡萄酒的评分过程中，应制定相应能够进行量化表述的一套客观标准(表4)。

表4 葡萄酒评价标准

对于其中的每一个指标Ci的评价级别和对应分值见表5。

表5 葡萄酒等级划分标准

根据专家经验给出对比矩阵:

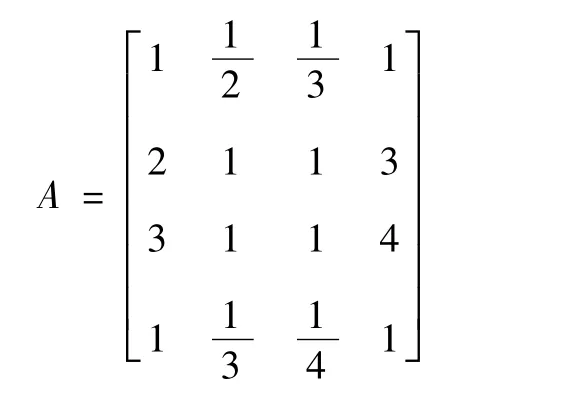
通过对矩阵A进行一致性检验，求得特征根λ为4.03，RI=0.9，一致性指标为CI=0.0103，RI=0.9，一致性指标=0.0115＜0.1，则一致性检测通过，并求得特征向量，并作归一化处理得到W=［0.139 0.341 0.404 0.116］。

3.4 评定成绩

以白葡萄酒样品为例，将品酒员所给的评分划分到对应的等级，而这5个等级对应的分值分别为95、85、75、65和50，共有十个品酒员对它打分，其中，

1≤i≤4，1≤j≤5，得到模糊评价矩阵为:

模糊子向量D:

做归一化处理，得到模糊子向量:

则样品1的最终得分为77.0329。

4 结束语

葡萄酒质量评价本身是一个不容易定量描述的问题，在评价中，品酒员受主观因素的影响较大，且打分过程中容易出现评价指标对不同葡萄酒权重不一致的不稳定情况。对于不同组品酒员之间，可以用方差分析，去解释是否存在显著性差异，同时，可以借助逆序数和肯德尔和谐系数去评定更加合理的一组。而直接处理品酒员们做出定量的分值并不合理，而定性的评价更为合理，所以需要借助于数学模型将定量的分值转化为定性的评价。最后，再依据对评价指标使用层次分析法得到权值与模糊矩阵进行运算，得到最终的分值。实验证明，本文所采用的方法可以将评委做出的定性描述转换为定量的分值，且最后计算得到的分值也更加科学合理，模型也存在两个不足。葡萄酒评价标准中可以再添加因素，但一致性检验不容易通过;同时，在得到一组数据更加合理的情况下，直接舍去了另一组数据，没有很全面的对数据进行利用。

［1］高媛媛，刘强国.基于LIBSVM的葡萄酒品质评判模型［J］.四川理工学院学报：自然科学版，2010，23(5)：530-532.

［2］王 星.非参数统计［M］.北京：清华大学出版社，2009.

［3］杨 萌，程铭东.排球赛积分方式的公平性评价分析［J］.山东体育学院学报，2011，27(4)：76-78.

［4］徐文彬.教育统计学［M］.南京：南京师范大学出版社，2007.

［5］Tong Y，Li Y J.The evaluation of enterprise informatization performance based on AHP J［C］.//Lan Hua.Proceeding of2007 International Conference on Management Science＆Engineering，Harbin Institute of Technology，Harbin，China，August20-22，2007：149-155.

［6］刘浩杰，赵长红，李存斌.基于AHP和模糊评价的研发人员绩效考核研究［J］.华北电力大学学报，2012，39(5)：105-108.

［7］张道文.汽车4S店销售服务顾客满意度评价模型［J］.西华大学学报：自然科学版，2011，30(6)：9-12.

［8］曹庆奎，阮俊虎，刘开第.基于隶属度转换算法的矿业投资决策模糊评价［J］.河北工程大学学报：自然科学版.2010，27(1)：92-95.

［9］谭长建.基于模糊综合评判法的桥梁监管评价体系研究［J］.四川理工学院学报：自然科学版.2012，25(3)：71-75.

［10］史 峰，王 辉，郁 磊，等.Matlab智能算法30个案例分析［M］.北京：北京航空航天大学出版社，2010.