基于QoS约束的网格任务调度算法
2013-11-04王浩,李飞
王 浩,李 飞
(成都信息工程学院网络工程学院,成都 610225)
引言
网格[1]环境下的任务调度问题是网格技术中的一个基本问题。由于网格环境中的资源所具有的异构性、动态性和分布性等特点,使得如何对任务进行调度以期满足各方面(系统用户、资源提供者、系统管理者等)的需求成为一个极具挑战性的问题。网格任务调度[2]的实质是将其环境中的m个需要调度的任务合理的分配到n个系统可用资源主机上去执行。由于现实环境中的网格系统规模一般都比较大,这样就决定了m和n都比较大,因此问题则转变成为一个NP难问题,即需要在有限时间内,在2n个资源集合中寻找出最优任务-资源匹配方案,然而这又是不可能实现的,因此,一般都采用启发式任务调度算法获取近似最优配对。
目前国内外所研究的调度算法一般分为在线模式(on-linemode)和批处理(batch mode)模式两类。在线模式在任务到达的第一时间执行映射。批处理模式则需将任务收集到一定数量(系统设定的一个参数数值),等待映射事件发生后才开始映射所收集的任务。
1 相关工作
本文主要研究的是批处理模式下的启发式任务调度算法,并且已假定各任务之间相互独立,各任务在不同的资源上运行的预测执行时间可知。目前,经典的批处理模式下的调度算法有:Max-min[3]算法、Minmin[3-6]算 法、GA[7-8]算 法、Sufferage[9-10]算 法 和SA[11](Simulated Annealing)等。Max-min算法是基于MCT(Minimum Completion Time,最小完成时间)的改进算法,算法选取最早完成时间最大的任务进行优先调度。GA算法与SA算法,其复杂度一般认为都比较高。对于QoS约束[12-14]下的任务调度算法,国内外已有不少研究成果,其都考虑了多QoS约束的问题,但是对于大量的QoS约束(来自于系统用户、资源提供者、系统管理者等方面的)并未进行细分讨论;并且考虑的QoS约束一般都比较少,其对新约束条件的扩展性也比较差。
Min-min算法也是基于MCT的改进算法,算法优先选择最早完成时间最小的任务进行调度,其以最快的速度减少任务调度队列中的待调度任务,以缩短任务的完成时间。但是Min-min算法同时也是一种贪心算法,仅追求任务完成时间最早的局部最优解,使得系统负载不均衡,导致时间跨度值变大。尤其当任务的执行时间差异较大的时候,产生的负面效应就越突出。任务的损失度值反映出任务在资源主机上的执行完成时间差异,反映了环境的异构性。Sufferage算法的时间跨度较小并且系统负载基本均衡,算法在减小任务调度跨度上的性能优于其它批处理算法,其表现出良好的综合性能;而对于具有QoS需求的任务的情况,基本欠缺考虑,并且任务本身也可能被多次进行分配。
在对多种异构环境下的启发式任务调度算法进行了研究、分析对比以后,结合Min-min算法和Sufferage算法的思想,提出了基于任务QoS约束和任务调度损失度的最小最早完成时间算法(QoSDimensions and Sufferage Min-min,QDSM)。本文将任务QoS约束与任务损失度引入Min-min算法中,在综合权衡任务最早完成时间、任务QoS约束与调度损失的基础上进行任务调度,使得算法更加适应于异构环境。仿真测试表明,QDSM算法具有较好的综合性能。
2 QDSM算法
2.1 参数定义
为了更好的说明QDSM算法,本文使用以下一般性定义:
定义1 集合T={t1,t2,…,tm}包含m个相互独立的任务。
定义2 集合H={h1,h2,…,hn}包含n个可用资源。
定义3 任务集合T所包含的m个任务在可用资源集合H所包含的n个主机上的预测执行时间(Expected Time to Compute,ETC)结果为m×n的矩阵:

元素eij表示待执行任务ti在可用主机资源hj上的预测执行时间。
定义4 m个待执行任务在n个可用资源上面的预测最小完成时间MCT结果为m×n的矩阵:
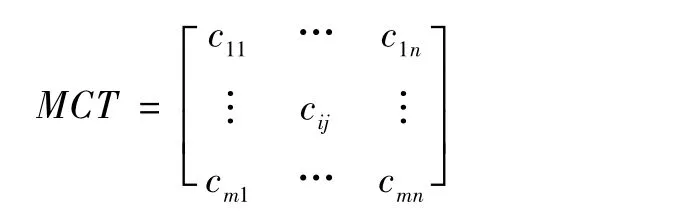
元素cij表示待执行任务ti在可用主机hj上的预测最小完成时间。
定义5 目前研究的用户QoS约束,考虑了4个维度:安全性、费用、成功率以及稳定性,映射为m×4的用户QoS约束(User QoSDimensions,UQD)矩阵:

定义6 集合V为待调度分配任务集合,其中,所有元素均属于T并且尚未被分配。
定义7 第i个任务ti的损失度(sufferage)为任务的最优最早完成时间与次优最早完成时间之差。即:

m个任务的suffer值构成了维度为m的向量S={s1,s2,…,sm}。
定义8 m×k维矩阵MT,用于储存每个任务在各个资源主机上的前k个最小执行时间,其中,元素mtij表示任务ti的最小完成时间,参数k为可调节参数,取值范围为[1,n]。
2.2 算法描述
根据前述参数定义,首先对UQD矩阵进行归一化处理,计算权重,选取权重最大者存入向量Q;分别选取待调度任务中的最小执行时间任务与suffer值最大的任务,分别进行标记;计算权衡系数α,根据权衡系数,选取相应的任务进行调度,同时更新MCT矩阵。
对于用户QoS约束矩阵UQD和预测执行时间矩阵ECT均已知,并已初始化;MCT矩阵和集合V均为空。算法的详细步骤如下:
(1)输入矩阵ECT和UQD。
(2)对矩阵MCT和集合V进行初始化,其中,MCT=ECT,V=T,对矩阵UQD进行归一化处理。
(3)在矩阵ECT中,查找每个任务的最小执行时间,并选取前k个元素存入矩阵MT。
(4)当V非空时,循环执行步骤(5)~步骤(9)。
(5)根据MCT矩阵,计算任务集合V的suffer值,并从中找出任务的最大suffer值,记为sa,其对应的任务ta∈V。
(6)在矩阵MT中,查找对应于任务集合V的最大执行时间任务,记为mtb,其对应的任务tb∈V,suffer值记为sb。
(7)对归一化后的UQD矩阵,计算任务的各维QoS约束在待调度任务中所占权重,选取所占权重最大者存入向量Q={mq1,mq2,…,mqm}。
(8)求解权衡系数α,

(9)如果(sa≥(α×sb))
将任务ta分配到资源主机ra上执行,并依据ta的执行时间更新MCT矩阵,从集合V中删除任务ta,否则,将任务tb分配到资源主机rb上执行,并依据tb的执行时间更新MCT矩阵,从集合V中删除任务tb。
3 性能分析
在多任务、多资源的网格模拟环境GridSim[15]中使用随机产生的ECT和UQD矩阵作为仿真输入,分别针对Min-min算法、Sufferage算法、SMM算法和QDSM算法进行任务调度仿真,采集模拟数据,分析每个算法的性能,针对性的验证了QDSM算法在最优跨度、资源平均利用率等方面的性能。其中,资源平均利用率按下式计算。

实验使用统计数据均值对算法性能进行分析,分成2组进行实验仿真验证。
3.1 时间跨度
图1为资源数为10时,在不同任务数下进行的仿真实验得到的makespan均值,资源数与任务数分别按10∶100,10∶200和10∶300进行匹配。

图1 makespan均值
分析图1数据可知,Sufferage算法、SMM算法和QDSM算法的makespan均值均少于Min-min算法。随着任务数量的增加,QDSM算法的性能略有下降,但与Min-min算法和SMM算法相比仍有较好的性能。
3.2 资源平均利用率
图2所示为,资源数为10时,在不同任务数下进行的仿真实验得到的资源平均利用率。
由图2分析可知,QDSM算法使得系统的资源平均利用率比SMM算法略有提升,较Min-min算法和Sufferage算法都表现出较好的性能。
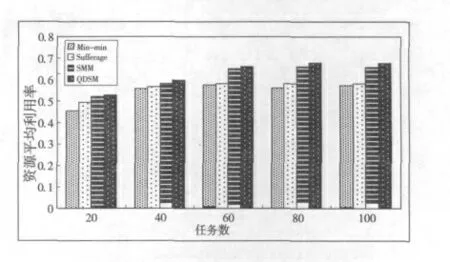
图2 资源平均利用率
4 结束语
本文在研究了多种启发式网格任务调度算法以后,提出了适合于异构环境的独立任务调度算法:基于任务QoS约束和任务调度损失度的最小最早完成时间算法(QoSDimensions and Sufferage Min-min,QDSM)。所提算法克服了Min-min算法的局限性,更适应于异构环境下的任务调度。然而,对于网格中资源的异常处理,需要分析异常产生的原因,根据原因有针对性的提出解决方案;对于任务约束的动态可扩展性,则需要对QoS约束、资源系统等各方面进行深入的分析与研究。
[1]都志辉,陈 渝,刘 鹏.网格计算[M].北京:清华大学出版社,2002.
[2]王相林,张善卿,王景丽.网格计算核心技术[M].北京:清华大学出版社,2006.
[3]Chauhan Sameer Singh,Joshi R C.A weighted mean time Min-Min Max-Min selective scheduling strategy for Independent Tasks on Grid[C].//Deepak Garg.Proceeding of IACC 2010,Patiala,India,February,19-20,2010:4-9.
[4]Braun T D,Siegel H J,Beck N.A comparison of eleven static heuristics for mapping a class of independent tasks onto heterogeneous distributed computing systems[J].Journal of Parallel and Distributed Computing,2001,61(6):810-837.
[5]周洋,蒋昌俊,方钰.异构环境下的独立任务调度算法的研究[J].计算机科学,2008,35(8):90-92.
[6]莫 赞,谢 娜,贾功祥,等.基于多QoS需求驱动的网格资源调度研究[J].计算机应用研究,2012,29(10):3904-3907.
[7]Braun T D,Siegel H J,Maciejewski A.Static mapping heuristics for tasks with dependencies,priorities,deadlines,and multiple versions in heterogeneous environments[C].Ibarra O H,Olariu S,Nakano K,et al.Proceedings of the 16thInt’l Parallel and Distributed Processing Symposium,F.L.,Florida,USA,April,15-19,2002:78-85.
[8]朱 海,王宇平.多目标约束的网格任务安全调度模型及算法研究[J].电子与信息学报,2010,32(4):988-992.
[9]He Xiaoshan,Sun Xianhe,von Laszewskig G.QoS Guided Min-min Heuristic for Grid Task Scheduling[J].The Journal of Computer Science and Technology,2003,18(4):442-451.
[10]李 炯,卢显良,董 仕.基于GridSim模拟器的网格资源调度算法研究[J].计算机科学,2008,35(8):95-97.
[11]薛胜军,徐钧磊,刑国稳.一种用于网格任务调度的退火进化算法[J].计算机应用研究,2011,28(11):4049-4052.
[12]Dogan A,Ozguner F.On QoS-based scheduling of a meta-task with multiple QoS demands in heterogeneous computing[C].Ibarra O H,Olariu S,Nakano K,et al.Proceedings of the 16thInt'l Parallel and Distributed Processing Symposium,F.L.,Florida,USA,April1,5-19,2002:50-55.
[13]Chauhan Sameer Singh,JoshiR C.QoSguided heuristic Algorithms for grid task scheduling[J].International Journal of Computer Applications,2010,2(9):24-31.
[14]Castillo C,Rouskas G N,Harfoush K.Online algorithms for advance resource reservations[J].Journal of Parallel and Distributed Computing,2011,71(7):963-973.
[15]Buyya R,MURSHED M.GridSim:a toolkit for the modeling and simulation of distributed resourcemanagement and scheduling for grid computing[J].Concurrency and Computation:Practice and Experience,2002,14(13):1175-1220.
