CH-γ方程的新的孤立尖波解

王丽芳

(镇江高等专科学校 数学教研室, 江苏 镇江 212003)

CH-γ方程的新的孤立尖波解

王丽芳

(镇江高等专科学校 数学教研室, 江苏 镇江 212003)

通过选取CH-γ方程中色散参数α和γ作为分支参数,基于平面动力系统的分支理论,利用相平面上特定的轨道,给出了该方程的一个新的孤立尖波解的解析表达式,证明了光滑孤立波和周期尖波解对孤立尖波解的收敛性质.

CH-γ方程; 孤立尖波解; 分支相图

0 引言

1993年,Camassa 和 Holm[1]考虑重力作用下,浅水层自由表面的水波运动,利用Hamilton原理导出了一类新型的浅水波模型

ut+2kux-uxxt+3uux=2uxuxx+uuxxx,

该方程简称为CH方程．他们发现该方程当k=0时有形如：

u(x,t)=cexp(-|x-ct|),

的孤立波解．这种形式的孤立波解因在波峰处一阶导数不连续,又被称为孤立尖波解．且他们预言当k≠0时不存在孤立尖波解．但Liu和Qian[2-3]基于动力系统分支方法,给出了该方程当k≠0时的孤立尖波解

Liu给出了该方程的另一个孤立尖波解

u(x,t)=(k+c)exp(-|x-ct)-k.

迄今为止,已有许多学者应用各种方法研究了CH方程及CH方程的一些广义形式[4-5]．最近,Dullin和Holm等[6-7]提出了如下广义CH方程

mt+c0ux+umx+2mux=-γuxxx,

其中m=u-α2uxx(α≠0),该方程又被称为CH-γ方程．显然此方程可重写为

ut+c0ux+3uux-α2(uxxt+uuxxx+2uxuxx)=-γuxxx

(1)

且当α2=1,c0=2k,γ=0时,方程(1)退化为CH方程．利用相平面分析方法,Guo和Liu[8]通过3种不同的途径获得了方程(1)的孤立尖波的解析表达式

u(x,t)=(c+γ/α2)exp(-|x-ct|/|α|),

和

u(x,t)=(c+γ/α2)[3exp(-|x-ct|/|α|)-2].

Tang和Yang[9],Zhang等[10]考虑积分常数的影响,进一步扩展了方程(1)的孤立尖波解．正如Guo和Liu[8]所说CH-γ方程比CH方程多两个参数,导致CH-γ方程包含的数字信息更复杂．

本文将通过选取方程(1)中的α和γ作为分岔参数,并考虑参数c0对行波解的影响,给出方程(1)一个新的孤立尖波解的表达式,并证明光滑孤立波和周期尖波解对孤立尖波解的收敛性质.

1 分支分析

令ξ=x-ct并将u(x,t)=u(ξ)代入方程(1),可得如下常微分方程

-cφ′+c0φ′+3φφ′-α2(φφ‴+2φ′φ″-cφ‴)=-γφ‴

(2)

对方程(2)关于ξ积分一次并忽略积分常数得

(3)

令y=φ′,可将(3)转化为

(4)

系统(4)存在奇直线

给分析带来不便,为此引入变换

dξ=(α2φ-cα2-γ)dτ,

在此变换下,系统(4)变为如下平面Hamilton系统

(5)

易于看出系统(4)和(5)具有相同的首次积分

H(φ,y)=(α2φ-cα2-γ)y2-φ3+(c-c0)φ2=h

(6)

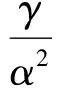
对于某一固定的h,式(6)确定了系统(5)的一族不变曲线;当h变动时,式(6)确定了系统(5)具有不同动力学性质的轨道族．令M(φe,ye)表示系统(5)的线性化系统在平衡点(φe,ye)处的系数矩阵,即

且在此平衡点处有

P(φe,ye)=trace(M(φe,ye))=0，

J(φe,ye)=det(M(φe,ye))=-(α2ye)2-(α2φe-cα2-γ)(3φe+c0-c),

由平面动力系统理论知,对于平衡点(φe,ye),若J(φe,ye)<0,则(φe,ye)是鞍点;若J(φe,ye)>0且P(φe,ye)=0,则(φe,ye)是中心;若J(φe,ye)>0且P2-4J>0,则(φe,ye)是结点;若J(φe,ye)=0且其Poincaré指标为0,则(φe,ye)是尖点．

基于上述事实作定性分析,得(α,γ)参数平面上的四条分支曲线:

注意当c>c0时,四条分支曲线满足不等式γ1(α)>γ2(α)>γ3(α)>γ4(α)．

基于以上讨论并利用向量场的分支理论,可得到如下描述系统(5)的平衡点的动力学行为的定理．

定理1 对于给定的c,c0(c>c0)及任意常数α,令

则有如下结论：

1) 当γ>γ1(α)时,系统(5)有四个平衡点(0,0),(φ1,0),(φ0,y±)．其中(0,0),(φ0,y±)是鞍点,(φ1,0)是被连接鞍点(0,0)的同宿轨道包围的中心;

2) 当γ=γ1(α)时,系统(5)有四个平衡点(0,0),(φ1,0),(φ0,y±)．其中(0,0),(φ0,y±)是鞍点,(φ1,0)是被连接鞍点(0,0),(φ0,y±)三条异宿轨道包围的中心;

3) 当γ2(α)<γ<γ1(α)时,系统(5)有四个平衡点(0,0),(φ1,0),(φ0,y±)．其中(0,0),(φ0,y±)是鞍点,(φ1,0)是被连接鞍点(φ0,y±)的轨道包围的中心;

4) 当γ=γ2(α)时,系统(5)有两个平衡点(0,0),(φ1,0)．其中(0,0)是鞍点,(φ1,0)是尖点;

5) 当γ3(α)<γ<γ2(α)时,系统(5)有两个平衡点(0,0),(φ1,0),且它们都是鞍点;

6) 当γ=γ3(α)时,系统(5)有两个平衡点(0,0),(φ1,0)．其中(0,0)是尖点,(φ1,0)是鞍点;

7) 当γ4(α)<γ<γ3(α)时,系统(5)有四个平衡点(0,0),(φ1,0),(φ0,y±)．其中(φ1,0),(φ0,y±)是鞍点,(0,0)是被连接鞍点(φ0,y±)的轨道包围的中心;

8) 当γ=γ4(α)时,系统(5)有四个平衡点(0,0),(φ1,0),(φ0,y±)．其中(φ1,0),(φ0,y±)是鞍点,(0,0)是被连接鞍点(φ1,0),(φ0,y±)三条异宿轨道包围的中心9) 当γ<γ4(α)时,系统(5)有四个平衡点(0,0),(φ1,0),(φ0,y±)．其中(φ1,0),(φ0,y±)是鞍点,(0,0)是被连接鞍点(φ1,0)的同宿轨道包围的中心．

系统(5)在不同区域的相图如图1所示．

(a)γ>γ1(α); (b)γ=γ1(α); (c)γ2(α)<γ<γ1(α); (d)γ=γ2(α);(e)γ3(α)<γ<γ2(α); (f)γ=γ3(c); (g)γ4(α)<γ<γ3(α); (h)γ=γ4(α)(i)γ<γ4(α).

2 CH-γ方程的新的孤立尖波解

本节通过相图中特定的轨道给出CH-γ方程一个新的孤立尖波解的解析表达式,表述为如下定理:

定理2 对于给定的c,c0(c>c0),则有

(7)

(8)

证明令Γ1表示图1(b)中经过(0,0),(φ0,y±)的三条直线轨道组成的三角形曲线,令Γ2表示图1(h)中经过(φ1,0),(φ0,y±)的三条直线轨道组成的三角形曲线．则Γ1可表示为

(9)

而Γ2可写为

(10)

将(9)和(10)代入系统(4)的第一个方程并分别沿Γ1和Γ2积分得

(11)

和

(12)

完成(11)和(12)中的积分,可得峰型孤立尖波与谷型孤立尖波的解析表达式(7)和(8)．

在系统(5)的相图中,三条异宿直线轨道组成的三角形对应方程(1)的孤立尖波解．在(7)中,当c0=0时,孤立尖波解与文[1]一致．(8)中的孤立尖波解从未在关于CH-γ方程的文献中出现过,是一个新的孤立尖波解的表达式．

3 其他行波解收敛到孤立尖波解的性质

本节首先给出光滑孤立波与周期尖波这两类行波解的解析表达式,并证明随参数γ的变化,这两类行波解将收敛到峰型或谷型孤立尖波解,表述为如下定理．

定理3 对于给定的c,c0(c>c0),则有

1) 对应于过鞍点(0,0)的同宿轨道,方程(1)有隐式峰型孤立波解

(13)

其中

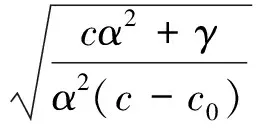
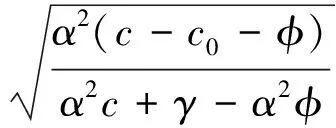
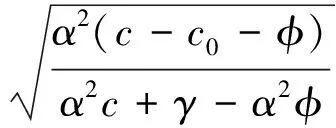
2) 当γ>γ1(α)且γ→γ1(α)时,隐式峰型孤立波解(13)收敛到峰型孤立尖波解(7)．

3) 对应于过鞍点(φ1,0)的同宿轨道,方程(1)有隐式谷型孤立波解

(14)

其中

4) 当γ<γ4(α)且γ→γ4(α)时,隐式谷型孤立波解(14)收敛到谷型孤立尖波解(8)．

证明如图1(a)与(i),由首次积分(6)知,过鞍点(0,0)和(φ1,0)的同宿轨道分别表示

(15)

和

(16)

将(15)和(16)代入系统(4)的第一个方程并分别沿相应的同宿轨道积分得

(17)

和

(18)

完成积分(17)和(18),即得隐式峰型孤立波解(13)和隐式谷型孤立波解(14)．

另外,我们有

和

因此,峰型孤立尖波解可由(7)当γ→γ1(α)时得到,而谷型孤立尖波解可由式(8)当γ→γ4(α)时得到．

4 结论

为了考查CH-γ方程(1)中色散参数对方程行波解的影响,我们选取该方程中色散参数α和γ作为分支参数,基于平面动力系统的分支理论,利用相平面上特定的轨道,给出该方程一个新的孤立尖波解的解析表达式,并严格证明了光滑孤立波和周期尖波解对孤立尖波解的收敛性质,从而丰富了对该方程的研究结果．

[1] Camassa R, Holm D D. An integrable sallow water equation with peaked solitons?[J]. Phys Rev Lett, 1993, 71(11):1661-1664.

[2] Liu Z R, Qian T F. Peakons of Camassa-Holm equation?[J]. Appl Math Modeling, 2002,26: 437-480.

[3] Liu Z R, Qian T F. Peakons and their bifureation in a generalized Camassa-Holm equation?[J]. Int J Birfurcation and Chaos, 2001,11(3):781-792.

[4] Liu Z R. Extension on the Peakons of Camassa-Holm equation?[J]. Yunnan University for Nationalities, 2004, 13(1): 3-9.

[5] Boyd J P. Peakons and Coshoidal waves: traveling wave solutions of the Camassa-Holm equation?[J]. Appl Math Comput,1997,81: 173-187.

[6] Dullin H R. An integrable shallow water equation with linear and nonlinear dispersion?[J]. Phys Rev Lett, 2001,87: 4501-4504.

[7] Dullin H R, Gottwald G A, Holm D D. On asymptotically equivalent shallow water wave equations?[J]. Physical D, 2004,190: 1-14.

[8] Liu Z R, Guo B L. Periodic blow-up solutions and their limit forms for the generilized Camassa-Holm equation?[J]. Progress in Nature Science, 2008,18: 259-266.

[9] Tang M Y, Yang C X. Extension on peaked wave solutions of CH-γequation?[J]. Chaos Solitons & Fractals, 2004,20: 815-825.

[10] Zhang L J, Chen L Q, Huo X W. Peakons and Periodic cusp wave solutions in a F Cooper H Shepard Solitons in the Camassa-Holm equation?[J]. Phys Lett A, 1994,194: 246-250.

NewSolitaryPeakonSolutionofCH-γEquation

WANG Li-fang

(Department of Mathematics, Zhenjiang College, Zhenjiang Jiangsu 212003, China)

By selecting the dispersion parameters αandγ in CH-γequation as the bifurcation parameter, based on the bifurcation theory of planar dynamical systems, using the particular track on the phase plane, gives the analytical expression of the new solitary peakon solution of CH-γequation, proves the properties of smooth solitary wave and periodic peakon solution converge to the solitary peakon solution

CH-γequation; solitary peakon solution; bifurcation phase portrait

2013-09-16

王丽芳(1968-)， 女， 江苏无锡人， 讲师， 硕士， 主要从事微分动力系统的研究.

O175.2

A

1671-6876(2013)04-0287-06

[责任编辑李春红]