Randomized Kaczmarz algorithm for CT reconstruction

ZHAO Ke(赵 可), PAN Jin-xiao(潘晋孝), KONG Hui-hua(孔慧华)

(School of Science, North University of China, Taiyuan 030051, China)

Randomized Kaczmarz algorithm for CT reconstruction

ZHAO Ke(赵 可), PAN Jin-xiao(潘晋孝), KONG Hui-hua(孔慧华)

(School of Science, North University of China, Taiyuan 030051, China)

The order of the projection in the algebraic reconstruction technique (ART) method has great influence on the rate of the convergence. Although many scholars have studied the order of the projection, few theoretical proofs are given. Thomas Strohmer and Roman Vershynin introduced a randomized version of the Kaczmarz method for consistent, and over-determined linear systems and proved whose rate does not depend on the number of equations in the systems in 2009. In this paper, we apply this method to computed tomography (CT) image reconstruction and compared images generated by the sequential Kaczmarz method and the randomized Kaczmarz method. Experiments demonstrates the feasibility of the randomized Kaczmarz algorithm in CT image reconstruction and its exponential curve convergence.

Kaczmarz method; iterative algorithm; randomized Kaczmarz method; computed tomography (CT); CT image reconstruction; exponent curve fitting

0 Introduction

Computed tomography (CT) is an imaging technique, related to radiation physics, mathematics, computer science, graphics, image science, mechanics and other multi-subject areas. CT is a revolutionary impact not only to diagnostic medicine, but also to the non-destructive testing, anti-summation materials organizational analysis and other industrial fields. There are many image reconstruction algorithms, here we mainly introduce the iterative method.

For CT, the object to be reconstructed is embedded in a regular discrete 2-D or 3-D pixel grid. The problems of image reconstruction from projections can then be represented by a system of linear equations[1]

where x=(x1,x2,…,xn)Tis the unknown image, the entries of the vector represent the unknown image intensity levels of beam attenuation in transmission tomography and so are naturally non-negative. y=(y1,y2,…,ym)Tis the measured projection data. The entries of the matrix A=(aij)m×nare the length of the intersection of the j-th pixel with the i-th ray, therefore aijis non-negative. Most of the pixels do not intersect with ray, so A is quite sparse.

The purpose of the reconstruction is to reconstruct the original image x from the observed data. A solution by direct method involving the matrix A might be infeasible because of the ill-posedness of the problem and huge data dimension in practice. One of the most popular solvers for such system is Kaczmars’s method, which is a form of alternating projection method. This method is also known under the name algebraic reconstruction technique (ART)[2]in CT.

The algorithm is written as

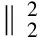
Iteratively, for each projection image ray, the grid is projected, the projection is compared with the corresponding ray value in the acquired projection image, and a correction term is computed and back-projected onto the grid[3]. Ideally, each back-projection updated the grid to correspond more closely to the acquired projection data. The iterative process is terminated when some errors of convergence-rate threshold are reached.

Because this algorithm applies only one ray to update the entire image at each step, the order in which the collected data can access during the reconstruction procedure has a large influence on the convergence rate of it.

Several observations[4-8]have been made on the improvements of the projection access systems，however these algorithms are quite appealing for applications, no guarantees of its rate of convergence have been known. Until recently, Strohmer and Vershynin proposed the first randomized Kaczmarz method with exponential expected rate of convergence[9]. In 2009, Censor and Herman pointed out that the reported success of the algorithm of Strohmer and Vershynin in their numerical simulation depends on the specific choices that are made in translating the underlying problem, whose geometrical nature is “ find a common point of a set of hyper-planes”, into a system of algebraic equations[10].

The aim of this paper is to apply the randomized Kaczmarz method to CT image reconstruction. This paper is organized as follows. A brief introduction of randomized Kaczmarz method and the algorithm applied in CT is given in section 1. Section 2 describes the basic setup of the comparison, including the phantom and simulation setup and the assessment of the reconstructed image accuracy, and presents quantitative results on image reconstruction accuracy. The conclusion is given in section 3.

1 Kaczmarz method

1.1 Randomized Kaczmarz method

The classical Kaczmarz method sweeps through the rows of the projection matrix A in a given order. The randomized Kaczmarz method is to set the probability proportional to the Euclidean norm of the row.

Let x0be arbitrary initial approximation to the solution of Eq.(1). The randomized Kaczmarz method is shown as

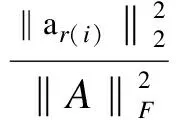
In 2009, Thomas Strohmer and Roman Vershynin proved the following exponential bound on the expected rate of convergence and the rate of convergence only depends on the scaled condition number for the randomized Kaczmarz method.

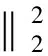
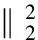
The inequality shows the exponentially convergence of the randomized Kaczmarz method.

1.2 Randomized Kaczmarz method for CT

Now, we apply the randomized Kaczmarz method to image reconstruction.

In the randomized Kaczmarz method assume that the linear system Ax=y is consistent or over-determined. However, in practice, especially for CT, the linear equation system may be underdetermined, or even if it is over-determined, the system may be inconsistent caused by the inherent noise in the acquired projection data.

Because of the sparsity of the projection matrix, the system of the equations is ill-conditioned problem. To solve the question, ATis deformated as

ATAx=ATy.

(5)

Obviously, Eqs.(1) and (5) have the same solution. The inequality Eq.(4) satisfies the condition of the randomized Kacamarz method. Here we let B=ATA.

Now, we prove Eq.(4) briefly[7].

First,

z=B-1Bz.

(6)

With the norm properties, we get

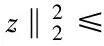
Then using the inner product, Eq.(7) can be written as

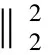
So Eq,(8) can be written as

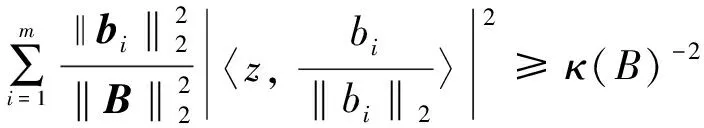
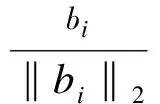
Then we get

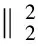
The two orthogonal vectors satisfy

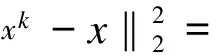
So

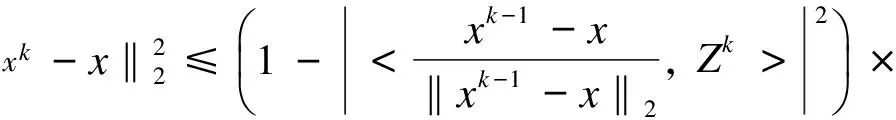
Here we take the expectation of both sides conditional on the choice of the random vectors Z1,…,Zk-1, namely.

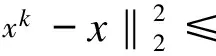
By Eq.(14) and the independence,

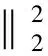
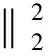
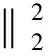
The proof is completed.

2 Simulation study

2.1 Phantom and simulation setup

Fig.1 Phantom of 2-D Shepp-Logan model

In our numerical study, the 2-D 64×64 pixels Shepp-Logan model is selected as the test model. The scanning range is 360°, and we choose 180 projection rays evenly. Pixel dynamic range is [0, 1]. The phantom is shown in Fig.1.

2.2 Assessment of image quality

In order to compare randomized Kaczmarz method with sequential Kaczmarz method, the following measure is calculated.

The mean square error is defined as[2]

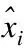
2.3 Results

We apply the Kaczmarz method and the randomized Kaczmarz method, respectively. We plot the mean square error (MSE) versus the number of iterations, and the results are shown in Fig.2.

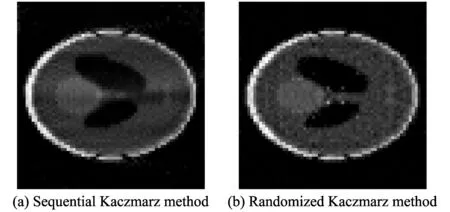
Fig.2 Reconstruction images after ten iterations

Fig.3 shows the reconstructed images after twenty iterations using the two iterative methods: sequential Kaczmarz method and randomized Kaczmarz method.

Fig.3 Reconstruction images after twenty iterations

Fig.4 and Fig.5 show the plots of the MSE as the function of the iteration number. Obviously, randemized Kaczmarz method shows a significantly faster convergence rate than sequential kaczmarz method. Otherwise, it can be seen that randomized Kaczmarz method converges in the exponentially curve form.

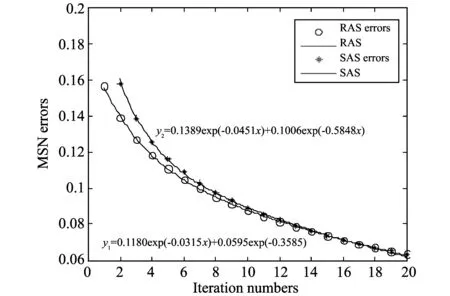
Fig.4 MSE as a function of iterations after twenty iteration

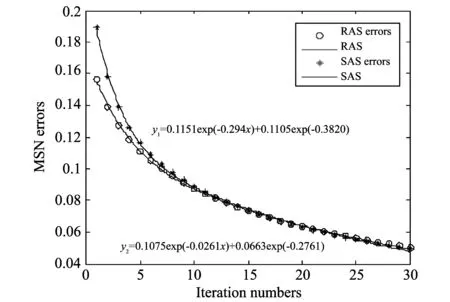
Fig.5 MSE as a function of iterations after thirty iterations

3 Conclusion

In this paper, randomized Kaczmarz method is introduced to improve the reconstruction speed and quality for parallel-beam CT. This algorithm has been evaluated using the simulation and the practical projection data for the parallel-beam x-ray CT. The results demonstrate that the proposed algorithm has the advantages of fast reconstruction speed and good quality. And it is also easy to implement.

[1] KONG Hui-hua. The accelerated iteration algorithm of image reconstruction. Taiyuan: North University of China, 2006.

[2] ZHUANG Tian-ge. CT principle and algorithm. First edition． Shanghai：Shanghai Jiao Tong University Press，1992: 2-93.

[3] Gordon R, Bender R, Herman G T. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and x-ray photography. Journal of Theoretical Biology, 1970, 29(3): 471-481.

[4] Herman G T. The fundamentals of computerized tomography. Academic Press, New York, USA, 1980, 101-122.

[5] Herman G T, Meyer L B. Algebraic reconstruction techniques can be made computationally efficient. IEEE Transactions on Medical Imaging, 1993, 12(3): 600-609.

[6] Byrne C L. Applied iterative methods. Wellesley, MA, USA, 2008: 209-277.

[7] Galántai A. On the rate of convergence of the alternating projection method in finite dimensional spaces. Journal of Mathematical Analysis and Applications. 2005, 310(1): 30-44.

[8] Bauschke H H, Deutsch F, Hundal H, et al. Accelerating the convergence of the method of alternating projections. Journal of the American Mathematical Society, 2003, 355(9): 3433-3461.

[9] Strohmer T, Vershynin R. A Randomized Kaczmarz algorithm with exponential convergence. Journal of Fourier Analysis and Applications, 2009, 15(2): 262-278.

[10] Censor Y, Herman G T, JIANG Ming. A note on the behavior of the Randomized Kaczmarz algorithm of Strohmer and Vershynin. Journal of Fourier Analysis and Applications, 2009, 15(4): 431-436.

date： 2012-09-25

National Natural Science Foundation of China (No.61171179，No.61171178)； Natural Science Foundation of Shanxi Province (No.2010011002-1，No.2010011002-2 and No.2012021011-2)

ZHAO Ke (ks2012@139.com)

CLD number： TN911.73 Document code： A

1674-8042(2013)01-0034-04

10.3969/j.issn.1674-8042.2013.01.008