Robust exponential stabilityanalysis of discrete-time switched Hopfield neural networks with time-varyingdelay
2013-11-01,
,
(School of Mathematics and System Science,Shenyang Normal University,Shenyang 110034,China)
0 Introduction
Switched systems are an important class of hybrid dynamical systems which are composed of a family of continuous-time or discrete-time subsystems and a rule that orchestrates the switching among them.Lots of valuable results in the stability analysis and stabilization for linear or nonlinear hybrid and switched systems were established;see[1-3]and the references cited therein.Recently,the switched Hopfield neural networks,whose individual subsystems are a set of Hopfield neural networks,have found applications in the field of combinatorial optimization,knowledge acquisition and pattern recognition[4-10].This motivated many researchers to study the stability issues of switched neural networks[11-15].In [14],the robust exponential stability analysis of discrete-time switched Hopfield neural networks with time delay is considered.However,the case of time-varying delay has not been available in the literature so far,which motivates us to carry out the present study.
1 Problem formulation and preliminaries
In this section,we will consider the model of discrete-time switched Hopfield neural networks with time-varying delay and uncertainty:

Whereσ(k)is a switching signal which takes its values in the finite setN={1,2,…,n}.u(k)=(u1(k),u2(k),…,un(k))T∈Rnis the state vector of the neurons,A=diag{a1,a2,…,an}are the state feedback coefficient matrix;B=(bij)n×nis the connection weight matrix.f(·)=(f(·),f(·),…,f(·))T∈Rnis the neuron activation function.The positive integerd(k)denotes the time-varying discrete delay satisfying

The initial condition associated with model(1)is given by
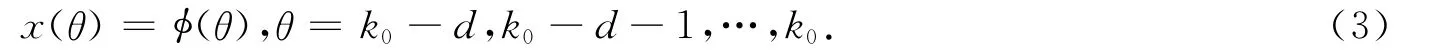
Throughout this paper,we have the following assumptions
1)Forj={1,2,…,n},the neuron activation functionsfj(·)are continuous and bounded.

3)The parameter uncertaintiesΔAi(k),ΔBi(k)are unknown but norm bounded,and satisfy

WhereFi(k)is an unknown real time-varying matrix and satisfies the following bound condition:

4)The switching sequence is defined asζ= {xk0;(i0,k0),(i1,k1),…,(im,km),…},whenk∈[k>m,km+1),theimth subsystem is activated and the states of system (1)do not jump when the switch occurs.
For our development,we need the following definitions and lemmas.
Definition 1[14]The discrete-time switched Hopfield neural network (1)is said to be robustly exponentially stable if its solution satisfies
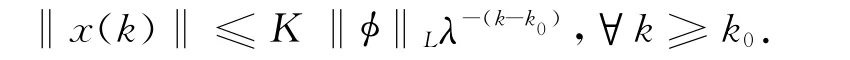
for any initial condition (k0,φ)∈R+×Cnand parameter uncertainty satisfying (5).‖φ‖L=supk0-d≤l≤k0‖φ(l)‖,K>0is the coefficient,andλ>1is the decay rate.
Definition 2[16]For anyk≥k0and any switching signalσ(s),k0≤s≤k,letNσdenote the switching numbers ofσ(s)during the interval[k0,k].If there existN0≥0andTa>0such thatNσ(k0,k)≤N0+(k-k0)/Ta,thenTaandN0are called the average dwell time and the chatter bound,respectively.
Without loss of generality,in this paper,we assumeN0=0for simplicity.
Lemma 1[3]For any constant matrixW=WT≥0,two positive integersrandr0satisfyingr≥r0≥1,the following inequality
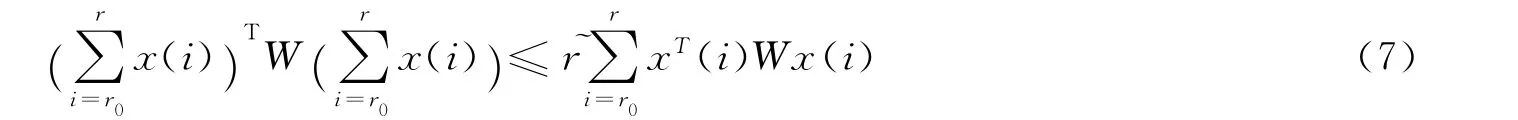
Lemma 2[17]LetA,D,MandWbe real matrices which have appropriate dimensions such thatW>0andFTF≤I.For any scalarε>0such thatW-εDDT>0,then we have the following inequality:(A+DFM)TW-1(A+DFM)≤AT(W-εDDT)-1A+ε-1MTM.(8)
2 Main results
In this section,the robust exponential stability criteria for the discrete-time switched Hopfield neural networks(1)will be presented using an average dwell time method.Firstly,consider the ithsubsystem ,that is,whenσ(k)=i,
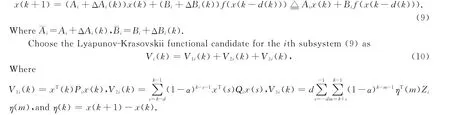
Now we give the following theorem,which plays an important role in the derivation of the robust exponential stability condition for system (1).
Theorem 1Under the assumptions(ⅰ)-(ⅳ),for given scalars 0<α<1,μ≥1,system (1)is robustly exponentially stable,if there exist diagonal matricesΛ=diag{λ1,λ2,…,λn}>0,and positive matricesPi>0,Qi>0,Zi>0,and scalarsε1i>0,ε2i>0,i∈N,such that the following inequalities hold:

Whicheidenotes the unit column vector having“1”element on itsith row and zeros elsewhere.Namely,
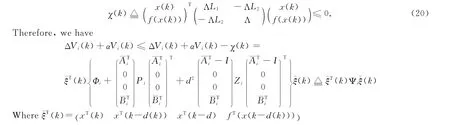
and

According to Definition 1,system (1)is robustly exponentially stable.This completes the proof of Theorem 1.
3 Illustrative examples
Example Consider the discrete-time switched Hopfield neural networks (1)with the following parameters:

E21=E22=E23=diag{0.03,0.04,-0.05},Fi(k)=diag{sin(k),sin(k),sin(k)},i=1,2,3,The activation functions are taken as

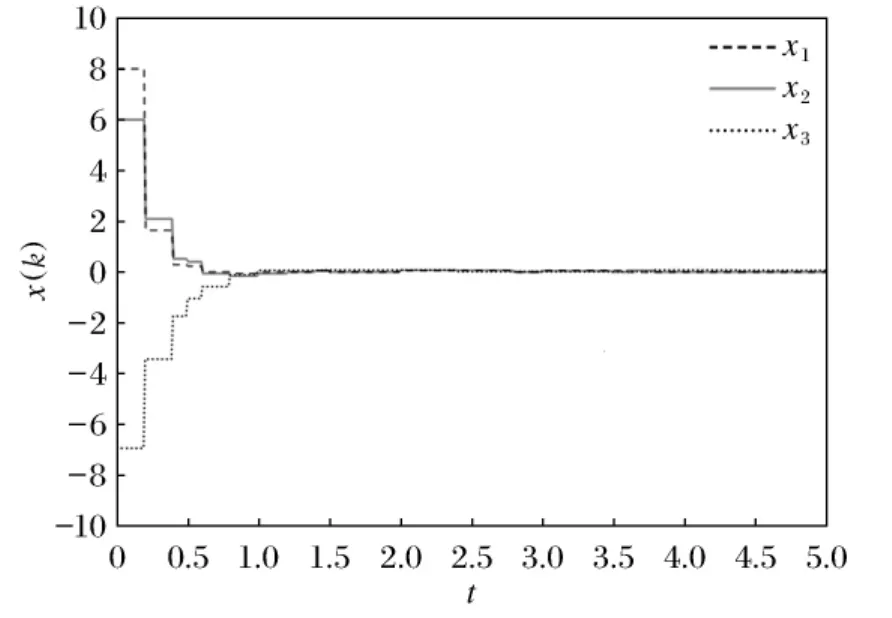
Fig.1 State of response of system (7)with(34)
Choosingα=0.4,μ=1.2,d=1.5,Solving the conditions(11),(12),(13),it is found that the linear matrix inequalities are feasible.We obtain that=0.3569,on the basis of(14),we have that=0.4is satisfied.
On the basis of (25),there are three subsystems in the switched system (1).In the simulation,let k0=0,d(k)=1.5*sin(k).Take the switching sequence as 321321321…….It can be seen from the switched sequence that Ta=0.5.
Choosing the initial value as φ(s)=[8 6 -7]T,we then obtain Fig.1,which depicts the trajectories of the system state.
4 Conclusions
This paper is concerned with the robust exponential stability problem for discrete-time switched Hopfield neural networks with time-varying delay and uncertainty.A numerical example is provided to demonstrate the potential and effectiveness of the results obtained.
[1]LIBERZON D,MORSE A S.Basic problems in stability and design of switched systems[J].IEEE Control Systems Magazine,1999,19(5):59-70.
[2]YE H,MICKEL N,HOU L.Stability theory for hybrid dynamical systems[J].IEEE Trans Autom Control,1998,43(4):461-474.
[3]李岩,刘玉忠.具有时变时滞不确定切换系统的鲁棒镇定[J].沈阳师范大学学报:自然科学版,2011,29(2):142-145.
[4]LI Hongyi,WANG Chuan,SHI Peng,et al.New passivity results for uncertain discrete-time stochastic neural networks with mixed time delays[J].Neurocomputing,2010,73(16/17/18),3291-3299.
[5]LIU Yurong,WANG Zidong,LIU Xiaohui.Asymptotic stability for neural networks with mixed time delays:the discrete-time case[J].Neural Netw,2009,22(1),67-74.
[6]WU Zhengguang,SHI Peng,SU Hongye.Delay-dependent exponential stability analysis for discrete-time switched neural networks with time-varying delay[J].Neurocomputing,2011,74(10):1626-1631.
[7]LIU Yurong,WANG Zidong,SERRANO A.Discrete-time recurrent neural networks with time-varying delays:Exponential stability analysis[J].Phys Lett A,2007,362(5/6):480-488.
[8]HUANG He,QU Yuzhong,LI Hanxiong.Robust stability analysis of switched Hopfield neural networks with time-varying delay under uncertainty[J].Phys Lett A,2005,345(4):345-354.
[9]ZONG Guangdeng,LIU Jia,ZHANG Yunxi.Delay-range-dependent exponential stability criteria and decay estimation for switched Hopfield neural networks of neural type[J].Nonlinear Analysis,2010,4(3):583-592.
[10]SUN Jian,LIU G P,CHEN Jie.Improved delay-range-dependent stability criteria for linear systems with time-varying delays[J].Automatica,2010,46(2):466-470.
[11]AHN C K.Switched exponential state estimation of neural networks based on passivity theory[J].Nonlinear Dyn,2012,67(1):573-586.
[12]LIAN Jie,ZHANG Kai.Exponential stability for switched Cohen-Grossberg neural networks with average dwell time[J].Nonlinear Dyn,2011,63(3):331-343.
[13]AHN C K.AnH∞approach to stability analysis of switched Hopfield neural networks with time-delay[J].Nonlinear Dyn,2010,60(4):703-711.
[14]HOU Linlin,ZONG Guangdeng,WU Yuqiang.Robust exponential stability analysis of discrete-time switched Hopfield neural networks with time delay[J].Nonlinear Analysis:Hybrid Systems,2011,5(3):525-534.
[15]ZHANG Dan,YU Li.Passivity analysis for discrete-time switched neural networks with various activation functions and mixed time delays[J].Nonlinear Dyn,2012,67(1):403-411.
[16]SONG Yong,FAN Jian,FEI Minrui,et al.RobustH∞control of discrete switched systems with time delay[J].Appl Math Comput,2008,205(1):159-169.
[17]XU Shengyuan,CHEN Tongwen.RobustH∞control for uncertain discrete-time stochastic bilinear systems with Markov switching[J].Internat J Robust Nonlinear Control,2005,15(5):201-217.
