捕食者具有传染病的捕食系统的全局稳定性

宋 燕，周 晶，张 宇

（渤海大学 数理学院，辽宁 锦州 121013）

0 引言与模型

传染病的存在是一种非常普遍的现象，对传染病传播规律的研究关系到国计民生。利用动力学方法建立传染病的数学模型，并通过数学模型对传染病进行定性与定量的分析和研究已取得了很多成果，这些成果主要集中在判定、预测疾病的发展趋势上，从而采取措施对疾病进行控制，参见文献［1－6］。然而，疾病可以在不同的种群之间传播，研究疾病在相互作用种群之间的传播规律，是种群生态学与传染病动力学的一种结合。文献［7］研究了疾病只在食饵中传播的生态－流行病模型，得到了疾病是否流行的阈值条件。文献［8－10］研究了捕食者有病的生态－流行病（SI）模型，研究了平衡点的稳定性。

文章研究捕食者和食饵均有密度制约，捕食者具有传染病，染病的捕食者不能捕食且染病捕食者染病之后可以恢复的生态－流行病（SIS）模型，模型如下：

其中S（t），I（t）表示t时刻捕食者种群易感者、染病者的数量，X（t）表示t时刻食饵的数量，r1为捕食系数，K1、K2分别为环境对食饵及捕食者的最大容量，r0为捕食者的内禀增长率，a0为食饵的内禀增长率，t1为转化系数，β为传染率系数，b1为染病者的恢复率系数，d1为染病者的死亡率（包括自然死亡率和因病死亡率），τ为时间变量，系统中各系数均为正数。

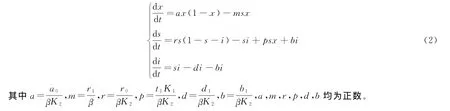
1 平衡点的存在性及解的有界性

定 理 1 系 统 （2）总 存 在 无 病 平 衡 点E0（0，0，0），E1（1，0，0），E2（0，1，0），E3时，系统（2）存在地方病平衡点当R0＞1时，系统（2）存在平衡点及地方病平衡点E5（x＊，s＊，i＊），其中：

为讨论解的有界性，引入引理1［11］。

引理1 在系统N′＝NF（N）中，如果函数F（N）满足条件：ⅰ）有唯一的正平衡点N＊，即存在N＊＞0，使F（N＊）＝0；ⅱ）当0＜N＜N＊时，有F（N）＞0；ⅲ）当N＞N＊时，有F（N）＜0，则平衡点N＊是全局稳定的。

定理2 系统（2）的满足初始条件（x（0），s（0），i（0））∈R3＋的所有正解是一致最终有界的。

证明 由系统（2）的第一个方程知x′≤ax（1－x），作辅助方程

由引理1知，对任意的ε，存在T，当t＞T时，有1－ε＜y（t）＜1＋ε。根据比较定理，存在T，当t＞T时，x（t）≤y（t）＜1＋ε。取V（t）＝x（t）＋s（t）＋i（t），当t＞T时，沿系统（2）的轨线对V（t）求全导数，有

作辅助比较方程

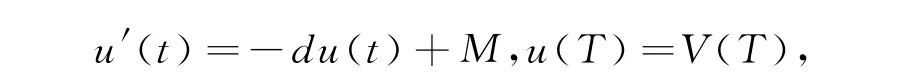
解之得

根据比较定理知

故存在M1及T′＞T，当t＞T′时，有V（t）＝x（t）＋s（t）＋i（t）≤M1。又因为x（t）≥0，s（t）≥0，i（t）≥0，从而满足初始条件（x（0），s（0），i（0））∈R3＋的正解是有界的。

2 无病平衡点的稳定性

定理3 系统（2）的无病平衡点E0，E1，E2是不稳定的；当时，无病平衡点E3是全局渐近稳定的，当R＞1时，E3是不稳定的。

证明 系统（2）的Jacobian矩阵为

系统（2）在E0处的Jacobian矩阵为

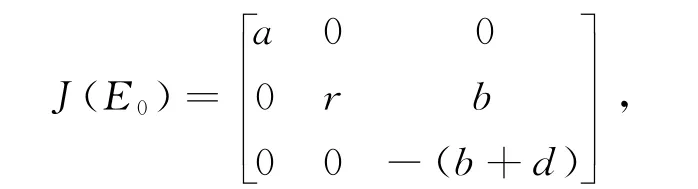
其特征根为λ1＝a，λ2＝r，λ3＝－（b＋d），有正的特征根，故E0不稳定。

同理，E1，E2也是不稳定的。

系统（2）在E3处的Jacobian矩阵为

所以λ1＜0，λ2＜0，从而当R≤1时，J（E3）特征根的实部均为非正，故E3是局部稳定的。当R＞1时，E3是不稳定的。

｛V′（t）＝0｝＝｛（，0）｝，故E3是V′（t）＝0的最大不变集，由LaSalle不变集原理得到E3是吸引的，从而E3是全局渐近稳定的。

3 地方病平衡点的稳定性

定理5 当R＞1时，地方病平衡点E5（x＊，s＊，i＊）是全局渐近稳定的。

证明 当R0＞1时，系统（2）除了地方病平衡点E5外，还存在平衡点E4，易证这时E4是不稳定的，因此下面只讨论地方病平衡点E5的稳定性。

系统（2）在E5处的Jacobian矩阵为

经计算可知H1＝a1＞0，H2＝a1a2－a3＞0，H3＝a3H2＞0，由 Hurwitz判据知，矩阵J（E5）的特征根的实部均为负的，所以地方病平衡点E5是局部渐近稳定的。

取Lyapunov函数

当且仅当x＝x＊，s＝s＊时，V′（t）＝0，这时i＝i＊，故由LaSalle不变集原理得到E5是全局渐近稳定的。

4 结 论

由上述讨论可知，在所讨论的模型中，系统的平衡点E0，E1，E2存在，但是不稳定。当a＞m时，亦即食饵的内禀增长率大于捕食系数时，系统存在无病平衡点E3，且当阈值R≤1时，无病平衡点E3是全局渐近稳定的，即疾病将逐渐消亡；当a＞m及R＞1时，系统存在地方病平衡点E5，且E5是全局渐近稳定的，即疾病流行，逐渐变为地方病。

［1］马知恩，周义仓，王稳地.传染病动力学的数学建模与研究［M］.北京：科学出版社，2004.

［2］HETHCOTE H，MA Zhien，LIAO Shengbing.Effects of quarantine in six endemic models for infectious diseases［J］.Math Biosci，2002，180：141－160.

［3］付景超，井元伟，张中华，等.具垂直传染和连续预防接种的SIRS传染病模型的研究［J］.生物数学学报，2008，23（2）：273－278.

［4］陈军杰.若干具有非线性传染力的传染病模型的稳定性分析［J］.生物数学学报，2005，20（3）：286－296.

［5］张敬，芦雪娟.一类具有非线性传染率的SEIQR流行病模型的全局稳定性［J］.数学的实践与认识，2011，41（16）：91－98.

［6］陈鑫，徐赫屿.一类具有线性传染力的SIRS传染病动力系统的分析与控制［J］.沈阳师范大学学报：自然科学版，2012，30（2）：153－156.

［7］黄友霞，王辉，苏丹丹.食饵有病的生态－流行模型的稳定性研究［J］.生物数学学报，2008，23（1）：132－138.

［8］杨建雅，张凤琴.捕食者有病的食饵－捕食者模型［J］.生物数学学报，2007，22（3）：419－424.

［9］孙树林，原存德.捕食者具有流行病的捕食－被捕食模型（SI）的分析［J］.生物数学学报，2006，21（1）：97－104.

［10］张拥军，王美娟，徐金瑞.捕食者具有传染病的捕食系统模型分析［J］.上海理工大学学报，2009，31（5）：409－413.

［11］马之恩.常微分方程定性与稳定性方法［M］.北京：科学出版社，2001.