波动率服从马尔可夫链的障碍期权差分格式

丁 华，周 经

（1.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030；2.安徽财经大学 国际经济贸易学院，安徽 蚌埠 233030）

期权的定价问题在金融数学和金融工程中一直是个热点问题。理想情况下可以假设标的资产价格服从几何布朗运动，波动率为常数；而许多实证分析表明波动率为常数的假设与具体期权市场的实际情况并不一致。本文假设波动率服从有限马尔可夫链[1]，利用有限差分格式，计算出一种障碍期权—上升敲出期权的价格。

1 模型假设

障碍期权是一种与路径有关的奇异期权，其收益不仅依赖期权到期日的标的物价格，还与整个期权有效期内标的物价格变化过程有关。障碍期权分为敲出期权和敲入期权。以上升敲出期权（up-and-out options）为例，在期权有效期内标的资产必须小于障碍价格，否则期权终止有效。投资人考虑到标的物价格S大于障碍价格B的概率较小，从而放弃了在S＞B时的期权收益，为此障碍期权比一般欧式期权价格便宜。

假设标的物价格S(t)服从如下分布：

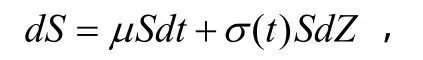
其中μ为收益率，dZ为标准维纳过程。波动率{σ(t),t≥0}是无后效性的随机过程，这里通过标的物收益的历史数据，可估计出波动率的k个状态

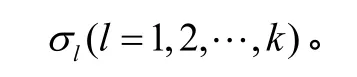
为此，构造出一步转移概率矩阵：

矩阵中元素

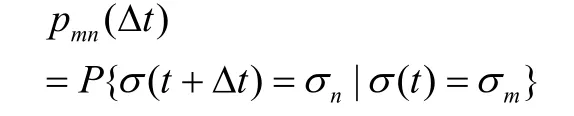
表示经过时间tΔ后波动率由mσ变为nσ的条件概率。N步转移概率

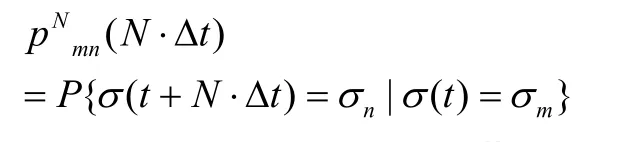
则为对应于N步转移概率矩阵NP 中m行n列的元素。

Ritchey[3]验证波动率服从 Markov链的欧式期权价格可以按波动率的概率分布为权重的 B—S定价公式的加权和进行计算。为此，本文运用有限差分法，进而得到波动率服从有限马尔科夫链的障碍期权定价的数值格式。

2 模型算法

上升敲出期权涉及两个风险资产：标的资产价格S，上升敲出期权价格 Vuo。假设执行价格为K，到期日为T，有效期[0,T]内资产的最高价格，B为障碍价格。显然满足条件：K＜B。在B—S模型下，Vuo解的表达式：

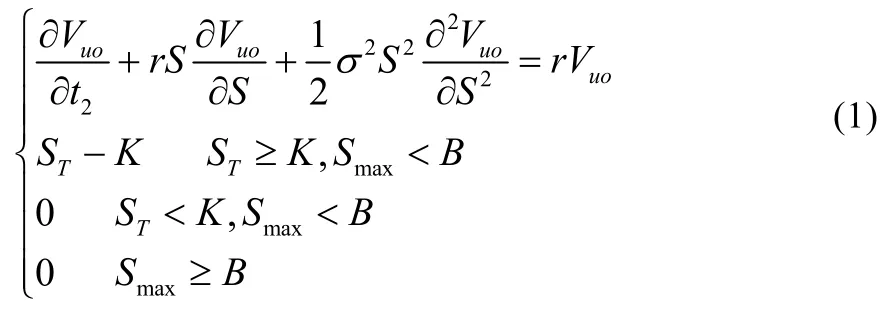
其差分格式具体方法如下。

对看跌期权价格的求解区域

进行等间隔的分割。假设

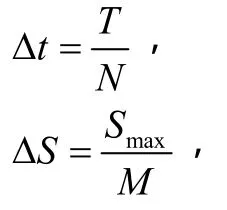
这样求解区域中就有了

个点的网格。如图1所示。

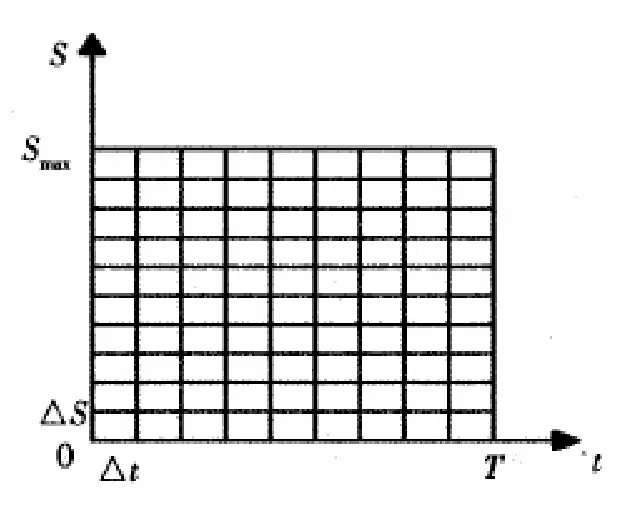
图1 求解区域的网格化

坐标上的点(i,j)表示时刻iΔt下标的物价格为jΔS，用变量Vuo表示点(i,j)的上升敲出期权价格。利用内含差分法，注意到

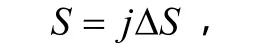
可得：

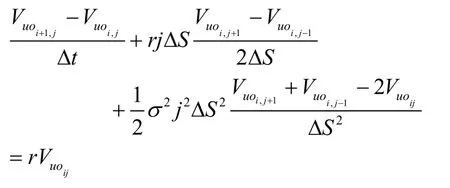
其中

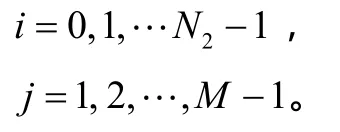
经过简单整理，并考虑 Vijuo边界条件有：

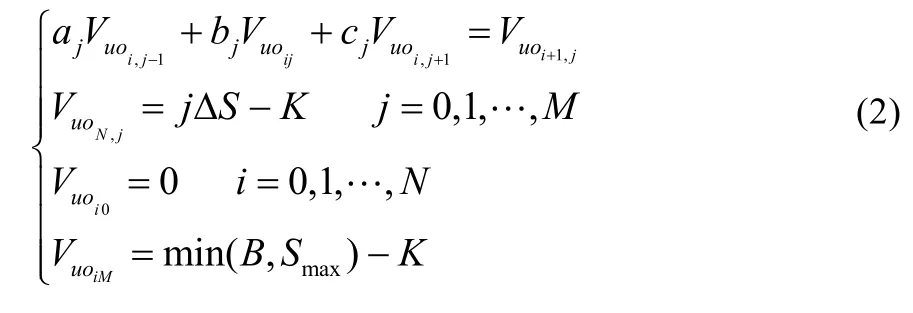
其中

根据(2)式，当1iN=-得到一个含有M-1个方程的方程组(3)：

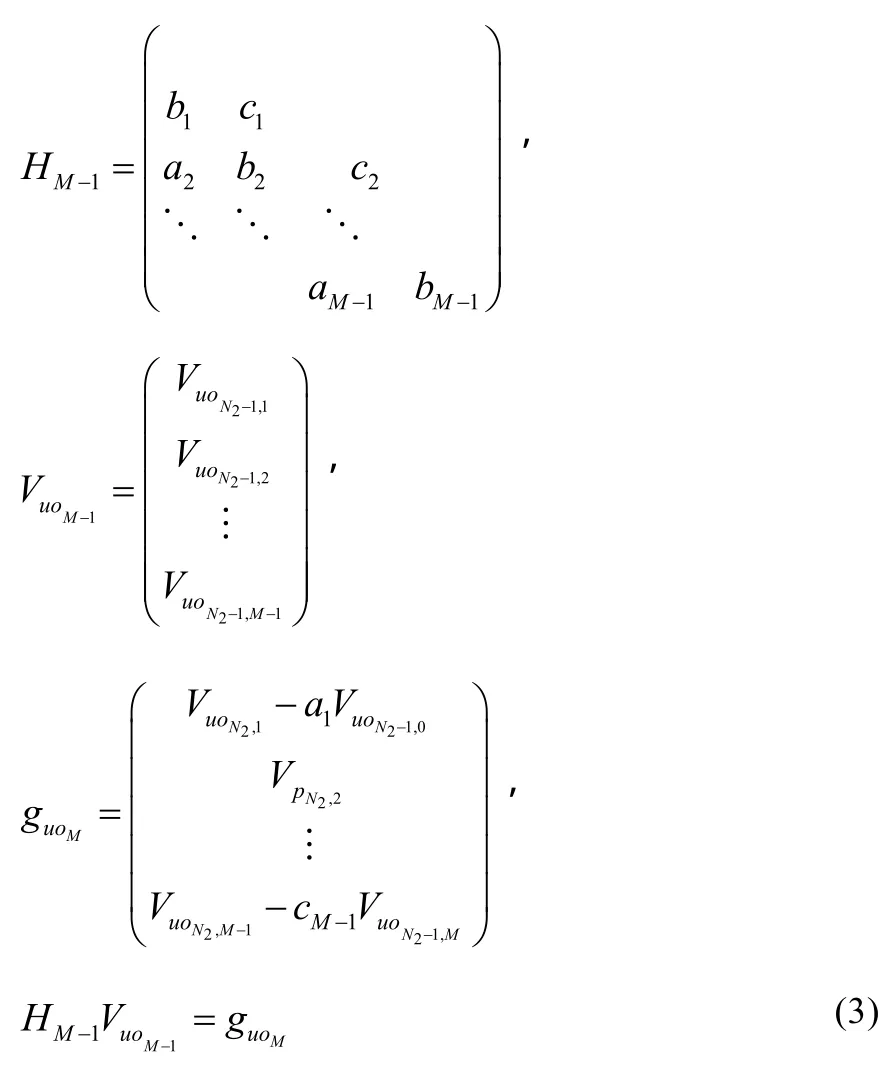
为此求解出与Tt-Δ时刻相对应的M-1个障碍期权的价格：

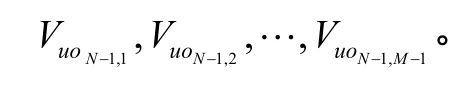
与 2Tt-Δ对应的结点也按同样方法处理，并以此类推。最终可以得到B-S模型下障碍期权值

由于标的资产波动率服从有限马尔科夫链，为此假设当前波动率为σl，同时考虑到历史波动率数据得到

在已知一步转移概率矩阵

的情况下，根据C-K方程可得到N步转移概率矩阵NP。其中取第l行元素

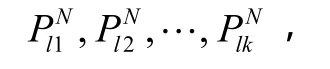
则上升敲出期权定价为：

其中

是B-S模型下波动率为nσ的上升敲出期权价格。

3 结束语

基于标的物波动率随机变化特点，假定波动率服从有限马尔科夫链，通过差分法，得到上升敲出期权的数值定价模型，修正了B-S模型的不足。不仅避免了一般随机波动率模型的复杂求解，而且计算也较简单，适用于不同类型期权交易的实际操作，具有一定的参考价值。

[1] Zhu Songping, Zhang Jin.A new predictor-corrector scheme for valuing American puts[J].Applied Mathematics and Computation.2011, 217(4): 439-452.

[2] Tangman D Y, Gopaul A, Bhuruth M.A fast high-order finite difference algorithm for pricing American options[J].Journal of Computational and Applied Mathematics,2008, 222: 17-29.

[3] Kwok Y k.Mathematical model of financial derivatives[M].Singapore: springer, 1998: 230-239.

[4] 李玉立,金朝嵩.美式看跌期权的差分格式[J].重庆建筑大学学报,2004,26(2):110-111.

[5] 叶中行,林建忠.数理金融[M].北京:科学出版社,1998:57-62.

[6] John C Hull.张陶伟,译.期权,期货和其他衍生产品(第三版)[M].北京:华夏出版社,2000:98-99.

[7] Joseph Stampfli.蔡明超,译.金融数学[M].北京:机械工业出版社,2004:45-49.

[8] Hull J C.期权,期货和其他衍生产品[M].北京:华夏出版社,1998:104-108.

[9] 李立康.微分方程数值解法[M].上海:复旦大学出版社,1999:45-48.

[10] 姜礼尚.期权定价的数学模型和方法[M].北京:高等教育出版社,2003:110-115.

[11] 唐小娅,王秀美,奚振斐,等.波动率服从马尔可夫链的期权定价[J].现代电子技术,2005(2):31-33.