高等数学中一类证明题的解题方法
2013-11-01周千
周 千
(西安航空学院 理学院,陕西 西安 710077)
1 引言
高等数学是理工类专业学生参加普通高等教育专升本考试的必考课程。每年考试的最后一题一般设置为证明题,旨在考查学生应用所学知识分析问题、解决问题的能力。笔者积累多年辅导专升本考试的经验,总结出了一些解决证明问题的常用而有效的方法。
2 证明题的常见类型及解题方法
在专升本高等数学的考试中,证明题的常见类型有两种,分别是:函数不等式的证明和适合某种条件下ξ的存在性问题的证明。
2.1 函数不等式的证明
对于函数不等式的证明,最常见的方法是利用函数的单调性证明不等式,其基本思路是:选取变量构造辅助函数,研究辅助函数的单调性。而构造辅助函数的基本思想是从欲证问题的结论入手,通过逆向分析,去寻找一个满足题设条件和结论要求的函数,一般是将待证不等式进行移向,使其右端为零,则左边的函数就是要构造的辅助函数。
例1:(2010年陕西省专升本考试·22题)证明:当x>0时,ex-ln(1+x)-1>xln(1+x)
分析:首先构造辅助函数,将不等式右端的项移至左边,使右端为零,则不等式变形为ex-ln(1+x)-1-xln(1+x)>0,令f(x)=ex-ln(1+x)-1-xln(1+x),即为辅助函数,然后分析其单调性即可证明原不等式。

而对于ex-1-ln(1+x),无法判断其正负,故应该继续求导。
设g(x)=ex-1-ln(1+x)(x>0)
总结:在解决有关函数不等式的证明问题时,利用导数研究辅助函数的单调性是解题的关键,但是在有些问题中,仅求一次导数是无法判断其单调性的,此时,需要进一步求导,然后将结果逆推,即可使待证不等式得到证明。
2.2 适合某种条件下ξ的存在性问题的证明
讨论中值存在性的一般方法是:先用逆向分析法寻求辅助函数,再验证该辅助函数满足某个微分中值定理的条件,从而由该定理结论导出欲证结果。在专升本考试中,最常用到的定理是罗尔中值定理。
常用辅助函数的构造步骤:①将欲证结论中的ξ变为x;②通过恒等变形将式子化为易于消去导数符号的形式;③ 通过观察法或积分法求出原函数(即不含导数符号的式子);④ 移项使等式一端为零,另一端即为所求辅助函数F(x)。
构造辅助函数的常用结论:
① 若方程为f(x)+xf′(x)=0,则令F(x)=xf(x);
② 若方程为f′(x)+λf(x)=0,则令F(x)=f(x)eλx;
③ 若方程为f′(x)+f(x)g′(x)=0,则令F(x)=f(x)eg(x);
对于①②③,我们可以总结为一个更加一般的结论:若方程为f′(x)+f(x)g(x)=0,则令F(x)=f(x)e∫g(x)dx,②③ 容易证明,我们仅证明 ①:

因此,对于适合某种条件下ξ的存在性问题的证明,都可以先转化为形如f′(x)+f(x)g(x)=0的形式,然后利用上述结论构造辅助函数F(x)。

分析:由f(c)=-cf′(c)可得,f(c)+cf′(c)=0,满足常用结论①,故令辅助函数F(x)=xf(x)。

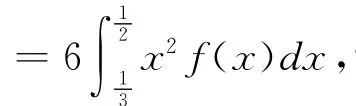

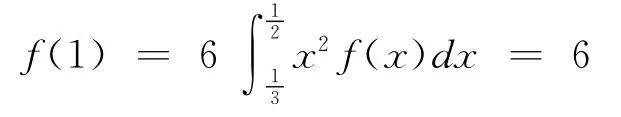
3 结语
对于专升本高等数学考试中的证明题,尤其是适合某种条件下ξ的存在性问题的证明,正确的构造辅助函数是解题的关键,应用本文给出的结论,能够很容易地构造出相应的辅助函数,对于学生正确解答证明问题显得非常的重要。
[1]华东师范大学数学系.数学分析[M].3版.北京:高等教育出版社,2003.
[2]裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,1993.
[3]同济大学数学系.高等数学:下册[M].6版.北京:高等教育出版社,2007.
[4]梅顺治,刘福贵.高等数学方法与应用[M].北京:科学出版社,2000.
[5]马知恩,王绵森.高等数学简明教程[M].北京:高等教育出版社,2009.
[6]上海师范大学数学系,中山大学数学力学系.高等数学:化、生、地类专业[M].北京:高等教育出版社,2010.
[7]钱吉林.数学分析题解精粹[M].北京:崇文书局,2003.
[8]岳忠玉,张绪绪.高等数学[M].3版.西安:西北大学出版社,2008.
