基于混沌和LWT－SVD的盲信息隐藏算法

张亚红，李志梅，覃 科

（桂林航天工业学院 信息工程系，广西 桂林 541004）

1 引言

随着信息媒体数字化和网络技术的飞速发展，越来越多的信息通过网络进行传输。然而如何保证秘密信息在网络上的安全传输，不被非法篡改、窃取和传播是迫切需要解决的问题。信息隐藏技术为信息的安全传输提供了一个有效的解决方案。它通常将秘密信息隐藏在载体的冗余信息中，以实现其不可感知和安全性，保护秘密信息不被未授权的第三方破解。

目前根据秘密数据的嵌入位置，信息隐藏可以分为基于空间域和基于变换域两种方法。前者算法实现简单，并具有很好的不易觉察性，但它的鲁棒性较差、安全性较低。相比而言，变换域算法具有抗攻击能力强的特点。主要包括离散傅里叶变换（DFT）、离散余弦变换（DCT）、离散小波变换（DWT）和Contourlet变换等。小波变换由于其时频特性及多尺度、多分辨率特性，应用较多［1－2］。周鹏颖等［1］提出一种基于小波－奇异值分解的数字水印新算法。该算法对原始图像进行多级小波分解后的部分子带作奇异值分解，并将水印置乱后再进行分块离散余弦变换，然后将它嵌入到中间奇异值及其周围的部分矩阵块中，鲁棒性较强。但该算法在提取信息的过程中需要原载体图像，不能盲提取，降低了通信的效率，并且实现比较复杂［3］。胡敏等［4］提出基于图像DCT域的信息隐藏盲提取算法。该算法根据人眼对图像DCT域的感知特性，对图像的DCT域系数进行特定的量化处理，将秘密数据隐藏在载体图像的DCT系数量化结果的奇偶特性上。算法简单，实现了盲提取，但是鲁棒性差。上述方法为了隐藏信息采用各种方法或多或少地都对原载体图像数据进行了修改，这样一来，信息的不可见性和保密性受到限制。马建湖等［5］提出基于小波变换的零水印算法。零水印［6］就是在嵌入水印的同时不改变载体图像，这种算法具有很强的不可见性和保密性，但它是利用图像的重要特征来构造水印信息，而不是修改图像这些特征，对于剪切、噪声、JPEG压缩等攻击具有较好的鲁棒性，但是对于旋转攻击鲁棒性差。

借鉴零水印的思想，结合小波和奇异值分解的特性，本文提出一种基于混沌的提升小波与奇异值分解的图像盲信息隐藏算法。实验表明，该算法保密性好，安全性高，对JPEG压缩、加噪、中值滤波、剪切、小角度旋转等有良好的鲁棒性。

2 相关理论

2.1 混沌理论

与传统加密方法相比，混沌序列具有良好的伪随机性以及对初值和参数的敏感性。用混沌序列对图像进行加密具有更高的安全性。其主要方法是利用混沌序列的大小关系对图像数据进行重排序，或者先把数字图像转换为二进制数据，然后利用混沌序列的二值化结果对图像二进制数据进行异或运算［7］。但是混沌序列是在无限精度的条件下获得，受到计算机有限字长的限制，实际产生的混沌序列常趋于周期性或收敛于不动点，这样数字化后容易产生短周期现象。为了克服有限精度问题，本文分别采用Logistic映射和王丽娜等［8］提出的混合光学双稳混沌模型生成混沌序列，将这两种混沌序列进行异或生成复合混沌序列，以避免数字化混沌系统动态特征退化，进而增加混沌序列的周期性和复杂度。然后用该复合混沌序列与秘密图像异或进行加密，从而增强秘密图像隐藏的安全性。

2.1.1 Logistic混沌映射

Logistic映射是一种被广泛使用的混沌映射，其映射迭代公式如下：

其中：Xn∈（0，1），μ∈（0，4］，当μ＞3.57时，从某个初值X0开始，迭代生成（0，1）区间均匀分布且无周期的混沌序列。

2.1.2 混合光学双稳混沌模型

下面的方程为混合光学双稳模型的迭代方程：

随着参数A，B的变化，系统将从固定点失稳，经倍周期分岔进入混沌。当参数A＝4，B＝2.5时，此时方程处于混沌状态。

2.2 提升小波变换

提升小波变换，也称为第二代小波变换，它继承了第一代小波的多分辨率的特征，小波变换后的系数是整数，计算速度快，计算时无需额外的存储开销。Daubechies已经证明，任何离散小波或具有有限长滤波器的两阶滤波变换都可以被分解成一系列简单的提升步骤，因此能够用Mallat算法实现的小波，都可以用提升算法来实现。提升小波变换的优点：图像的恢复质量对输入序列的长度没有任何限制，具有对任意尺寸图像进行变换的能力；小波的构造完全在空域内进行，无需傅里叶分析理论；运算速度快，节省存储空间；能够实现整数到整数的变换［9］。

2.3 奇异值分解

从线性代数的角度来看，一幅数字图像可以看成是由许多非负标量项组成的矩阵。设A∈Rn×n来表示一个图像矩阵，对矩阵A进行奇异值分解：

其中：U和V是正交矩阵，Σ为对角矩阵，其对角线上的元素σ1，σ2，…，σn称为矩阵A 的奇异值，且满足：σ1≥σ2≥ … ≥σr≥σr＋1＝… ＝σn＝0，r是A的秩，其为非负奇异值的个数。

在数字图像处理中，奇异值分解有两个重要特性：①图像的奇异值稳定性非常好，当图像遭到小的扰动时，图像的奇异值不会有太大的变化。周波等［10］从理论上证明，图像的奇异值对几何失真（转置、镜像、旋转、放大、平移）具有稳定性。②图像奇异值所表现的是图像的内蕴特性，即图像矩阵元素之间的关系而非视觉特性［3］。由于奇异值有上述特性，将秘密信息嵌入奇异值中，可以提高秘密信息受攻击的鲁棒性。本文算法利用奇异值的特性，对图像先进行提升小波变换，再对小波低频系数进行分块奇异值分解，利用块中最大奇异值的最高位的奇偶性生成图像特征信息，以实现秘密信息的隐藏。在此过程中不对载体图像做任何的修改，因此秘密图像具有良好的不可见性。

3 信息的隐藏与提取

3.1 秘密信息的隐藏

为了提高秘密信息的安全性，以及抗压缩、剪切、加噪等攻击的鲁棒性，本文先对秘密信息进行混沌加密处理。为了既能嵌入较大容量的秘密信息又能有好的鲁棒性，将载体图像进行1级提升小波变换。考虑到人眼对蓝色分量最不敏感，因此对蓝色低频子带系数进行分块奇异值分解。其次考虑到对最大奇异值修改，将严重影响载体图像的质量，所以不修改最大奇异值。而是根据最大奇异值最高位的奇偶性的特征来隐藏秘密信息，并不对载体图像进行修改，因此对秘密信息来说具有良好的隐蔽性。具体步骤如下：

设载体图像为M×M的RGB图像，秘密图像为N×N的256级灰度图像，隐藏过程如下：

（1）利用Logistic混沌映射和混合光学双稳模型生成复合混沌序列H（i）。

（2）将秘密图像由二维变成一维序列G（i），用复合混沌序列H（i）对其进行混沌加密。

（3）对载体彩色图像进行1级提升小波变换，提取蓝色分量低频子带小波系数。

（4）对蓝色低频子带小波系数进行2×2分块，然后对每个分块进行奇异值分解。当每块中最大奇异值最高位是奇数时，K（i）＝1（i＝1，...，n），否则K（i）＝0。

（5）通过以下的公式隐藏秘密图像，生成秘钥S（i）：

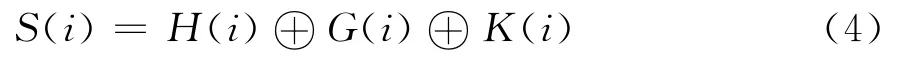
其中，H（i），G（i）都是二进制整数［5］，⊕ 为异或运算。Logistic混沌映射参数μ，X0，混合光学双稳模型参数A，B，Z0和S（i）一起构成最终的秘钥组。

3.2 秘密信息的提取

利用秘钥组中的S（i），按照下面的公式提取秘密图像G（i）：

4 仿真实验结果与安全性分析

仿真实验在MATLAB7.10的平台上进行，使用512×512的彩色图像Lena为载体图像（见图1），秘密信息为128×128的灰度图cameraman，提升小波采用haar小波基。原始秘密图像和加密后的秘密图像如图2所示。混沌映射中的参数：μ＝3.93，X0＝0.45，Z0＝0.4，A＝4，B＝2.5。未受攻击时从载体图像中提取的秘密图像如图2所示。

图1 原始载体图像

图2 未受攻击提取的秘密图像

采用归一化相关系数NC来衡量提取的秘密图像与原始秘密图像之间的相似程度。本算法对高斯噪声、椒盐噪声、滤波、剪切，小角度旋转、压缩等常见的图像攻击具有较好的鲁棒性（见表1）。

表1 各种常见攻击后提取的秘密图像

与张仁昌［11］、龚劬［12］等提出的算法相比较，本文算法在抗旋转、剪切、压缩方面的鲁棒性强，噪声攻击方面比龚劬等［12］提出的方法较强（见表2）。在信息的隐藏量方面，本文算法较张仁昌［11］、龚劬［12］等大，不可见性和安全性更好。

表2 各种常规攻击的实验结果

为了验证该算法的有效性，本文又分别以pepper，airplane，boat三幅512×512的彩色图像为原始载体图像（见图3）。按照本文算法隐藏秘密图像，然后经过多种攻击后提取秘密图像。从受攻击图像中提取的秘密图像的归一化相关系数NC（见表3）。

图3 不同载体图像

表3 不同载体图像各种攻击下的实验结果

该算法先使用复合混沌序列对秘密图像，如图4（a）所示，进行加密结果如图4（b）所示。使用原始加密数据进行解密，初值和参数为μ＝3.93，X0＝0.45，Z0＝0.4，A＝4，B＝2.5，解密结果如图4（c）所示。混沌加密算法的安全性主要在于初值和参数的个数比较多，即使其中几个数据是正确的，只将Z0＝0.4＋10－9，比原先增加了10－9，其它数据均与原始数据相同进行解密所得结果如图4（d）所示。验证了混沌系统初始值的微小变化也会得到完全不同的解密结果。

图4 秘密图像

如果采用穷举法攻击，混沌系统的初始值和参数的取值范围为整个实数域，混合混沌序列的密钥由5个浮点数组成，如果采用32位的浮点数表示，该密钥共需要160位，此时穷举法的密钥空间为2160，加密后的密图是128×128，密钥空间为16384！，要同时破解这两个密钥空间，几乎是不可能的，因此其安全性非常可靠。

5 结语

在信息隐藏的盲提取方面，大多都是对二值图像信息的提取，这些方法隐藏的信息量相对较低。本文提出一种基于混沌和LWT－SVD的盲信息隐藏算法。对载体图像进行提升小波变换，提取蓝色分量低频子带并分块奇异值分解，根据每块最大奇异值最高位的奇偶性隐藏秘密图像，并不修改载体图像。在提取秘密图像时，不需要原始载体图像，实现了真正的盲提取。该算法是对灰度图像进行隐藏和提取，隐藏的信息量较大。秘密图像嵌入之前采用复合混沌加密，保证了秘密图像的安全性。实验结果表明，该算法保密性好，信息隐藏量大，算法简单，能有效抵抗加噪、滤波、剪切、小角度旋转、JPEG压缩等攻击，具有良好的安全性和鲁棒性。下一步的工作将是提高大角度旋转的鲁棒性。

［1］甘甜，冯少彤，聂守平，等.基于分块离散小波变换的图像信息隐藏与盲提取算法［J］.物理学报，2012，61（8）：1－7.

［2］胡青，龙冬阳，卢伟.一种改进的小波系数差异量化水印算法［J］.计算机科学，2010，37（11）：261－264.

［3］周鹏颖，沈磊，田小林，等.基于小波—奇异值分解的数字水印新算法［J］.计算机应用研究，2010，27（5）：1896－1898.

［4］胡敏，平西建，丁益洪.基于图像DCT域的信息隐藏盲提取算法［J］.计算机工程与应用，2003，5：89－91.

［5］马建湖，何甲兴.基于小波变换的零水印算法［J］.中国图象图形学报，2007，12（4）：581－585.

［6］温泉，孙锬锋，王树勋.零水印的概念与应用［J］.电子学报，2003，31（2）：214－216.

［7］焦问，丁文霞.一种基于混沌映射和奇异值分解的数字图像水印算法［J］.信号处理，2011，27（8）：1219－1123.

［8］王丽娜，郭迟，李鹏.信息隐藏技术实验教程［M］.武汉：武汉大学出版社，2004.

［9］陈光喜，尹柳，易招师.基于整数提升小波变换的多功能数字水印［J］.计算机工程与应用，2011，46（11）：115－118.

［10］周波，陈健.基于奇异值分解的、抗几何失真的数字水印算法［J］.中国图象图形学报，2004，9（4）：507－512.

［11］张仁昌，耿国华.基于奇异值分解和小波变换的抗几何失真数字水印新方法 ［J］.计算机应用与软件，2007，24（6）：78－81.

［12］龚劬，马素春.基于分块奇异值分解的小波域水印算法［J］.计算机仿真，2009，26（5）：138－142.