基于太极形介质柱六角光子晶体禁带特性研究*

2013-10-30沈娟娟何兴道刘彬李淑静

物理学报 2013年8期

沈娟娟何兴道刘彬李淑静

(南昌航空大学,无损检测技术教育部重点实验室,南昌 330063)

1 引言

光子晶体[1,2]是一种介电常数空间周期性变化,能够控制光子行为的一种人工结构.它最突出的特点就是具有光子带隙[3,4],而频率处于带隙内的光是禁止传播的.基于光子晶体对光的可控性,光子晶体器件的应用得到了很大发展,如光子晶体光纤[5-9]、光子晶体波导[10-13]、光子晶体波分复用器[14]以及高效率的光二极管[15-20]等.一般而言,光子带隙越宽,光子晶体器件性能越稳定,所以理论上研究光子晶体带隙特性对光子晶体器件的设计具有重要意义.影响光子晶体带隙特性的可控因素有:材料相对介电常数、晶格填充比、散射子结构等[21-29].本文即是通过改变这些因素来改变光子晶体的带隙特性.目前对光子晶体带隙的计算方法主要有平面波展开法[30,31]、时域有限差分法[32]、传输矩阵法[33]等.由于二维光子晶体易制备[34-36]、在可见光范围内易产生禁带,所以其相关光学器件在光学集成、光信息传输及处理等光通信领域被广泛应用,而我们的研究为其理论设计和实际应用提供了依据.

目前已有很多关于二维光子晶体带隙宽度的研究,但他们采用的散射子模型的对称性较高,且很少关注带隙数量的变化.本文中,我们彻底打破散射子对称性,提出了一种新型的二维六角晶格光子晶体散射子结构--太极形散射子,采用平面波展开法,通过研究其参数ε,R,r/R,θ对带隙特性的影响,来获得最大的完全带隙宽度及最多的完全带隙数目.

2 模型

传统的光子晶体介质柱采用的是圆形,本文彻底打破散射子的对称性,构建了一种太极形介质柱在空气中周期排列组成的二维六角晶格光子晶体.为便于分析,设定光子晶体结构晶格常数a=1µm.如图1所示,R为大圆半径,r为内部两小圆半径,θ为两小圆圆心的连线与水平方向的夹角,设定θ沿顺时针方向为正.通过依次改变ε,R,r,θ来研究太极散射子六角光子晶体的带隙特性.

图1 (a)HLPC太极散射子介质柱结构;(b)太极散射子单个元胞

3 结果分析

一般来说,影响光子晶体带隙宽度和数量的因素有填充比、介电常数对比度、晶格结构等.太极形六角光子晶体完全打破了散射子对称性,具有较好的带隙特性.现在我们考虑不同介电常数对比度及其结构参数对其完全带隙宽度和数目的影响.设定 R=0.448µm,r=0.2R,θ=0◦,从 1-40改变介电常数对比度,扫描间隔,采用平面波展开法分析得到太极散射子带隙特性如图2(a)所示.图2(b)给出光子晶体完全禁带最大宽度的变化情况.可以看出:当ε≤6时,不存在完全光子禁带;ε=17时,完全光子禁带宽度获得最大值0.0348(ωa/2πc).从图2(a)可以看出:随介电常数对比度的增大,光子晶体完全带隙向低频方向移动,光子晶体完全禁带数目向介电常数对比度大的方向移动.所以太极散射子光子晶体要得到尽可能多的光子带隙,就要尽可能地选择介电常数较大的介电材料.

图2 (a)R=0.448µm,r=0.2R,θ=0◦时太极散射子带隙随ε的变化;(b)最大完全带隙随ε的变化;(c)ε=17,r=0.2R,θ=0◦时太极散射子带隙随R的变化;(d)最大完全带隙随R的变化关系;(e)ε=17,R=0.38µm,θ=0◦时太极散射子带隙随r的变化;(f)最大完全禁带宽度随r的变化关系;(g)ε=17,R=0.38µm,r=0.36R时太极散射子带隙随θ的变化;(h)最大完全带隙随θ的变化

影响太极形六角光子晶体带隙宽度的几何参数有:大圆半径R,小圆半径r以及旋转角度θ.通过依次改变这些参数,讨论获得最大禁带宽度的最优结构.基于介电常数对比度对光子带隙特性影响的分析,设定ε=17,r=0.2R,θ=0◦,从0-0.5µm,以间隔0.01来扫描光子晶体带隙特性,如图2(c)所示.图2(d)给出了光子晶体完全禁带最大宽度随R的变化关系:随半径增大,完全禁带向低频方向移动;R=0.38µm时,存在5条完全禁带,最大宽度为0.0437(ωa/2πc),介于归一化频率0.648-0.6917之间.

设定ε=17,R=0.38µm,θ=0◦,从0到 0.5R改变r,扫描间隔0.01R,太极形光子晶体带隙特性如图2(e)所示.可以看出:在小圆半径r的整个变化范围内都存在完全光子禁带.图2(f)为最大完全带隙宽度随r/R的变化图,当r=0.36R时,获得最大完全禁带,宽度为0.0541(ωa/2πc).

基于以上计算,设定ε=17,R=0.38µm,r=0.36R,从-90◦-90◦间隔 1◦分析旋转角度 θ对太极形光子晶体完全带隙特性的影响.如图2(g)所示,在θ的整个变化范围内都存在完全禁带.从图2(h)可以看出:当θ=0◦时,获得最大完全禁带,宽度为 0.0541(ωa/2πc).

此时我们得到了太极散射子六角光子晶体获得最大完全禁带时的最优结构参数:当ε=17,R=0.38µm,r=0.36R,θ=0◦时,获得最大完全禁带宽度0.0541(ωa/2πc),介于归一化频率0.6165-0.6706之间,其能带特性如图3所示.

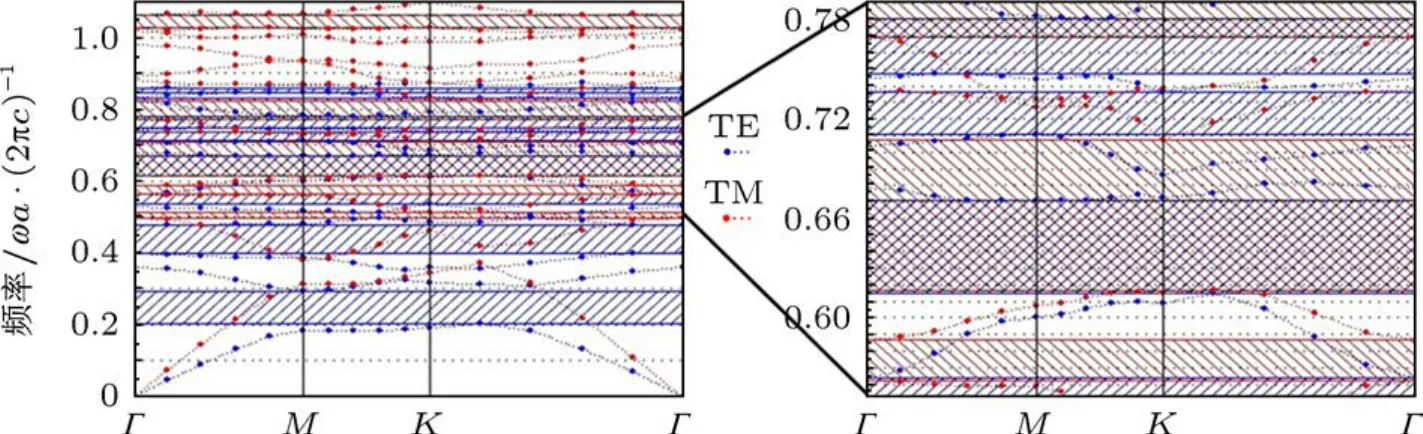
图3 ε=17,R=0.38µm,r=0.36R,θ=0◦时太极散射子能带图

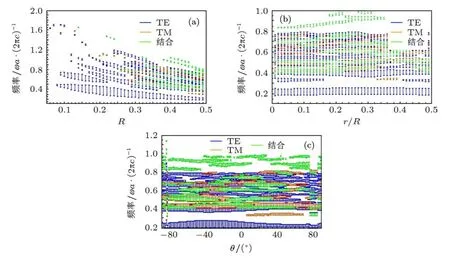
图4 (a)带隙数量随R的变化;(b)带隙数量随r的变化;(c)带隙数量随θ的变化

光子晶体散射子几何结构参数对带隙特性的影响除了禁带宽度还有禁带数目.基于之前的分析,太极散射子光子晶体的完全禁带向介电常数对比度大的方向移动,所以为了便于研究,设定ε=16来讨论结构参数R,r,θ对禁带数目的影响.首先在r=0.2R,θ=0◦时,以间隔0.01扫描R的值,计算结果如图4(a)所示,光子晶体完全禁带向低频方向移动.当R＜0.22时,光子晶体不存在完全禁带;当0.22≤R≤0.31时,仅有1条完全禁带;之后完全禁带数目逐渐增多,当R=0.44时,完全禁带数目最多,为8条.然后设定ε=16,R=0.44,θ=0◦,从0-0.5以间隔0.01扫描r/R的值,带隙分布随r/R变化情况如图4(b)所示.可以看出,在整个r变化范围内,太极散射子都存在完全禁带,r=0.2R时,完全禁带条数最多,为8条.最后在R=0.44,r=0.2R时,讨论旋转角度θ在-90◦-90◦变化范围内的带隙分布.如图4(c)所示,在θ的整个变化范围内都存在完全禁带,当θ=0◦时完全禁带条数最多,为8条.

此时我们得到了获得最多完全禁带数目时的结构参数ε=16,R=0.44,r=0.2R,θ=0◦,带隙特性如图 5所示,太极散射子结构存在8条完全禁带,分别介于归一化频率0.4032-0.4157,0.4353-0.461,0.4848-0.5188,0.595-0.619,0.665-0.6726,0.7-0.7009,0.7258-0.7495,0.7573-0.7703之间.

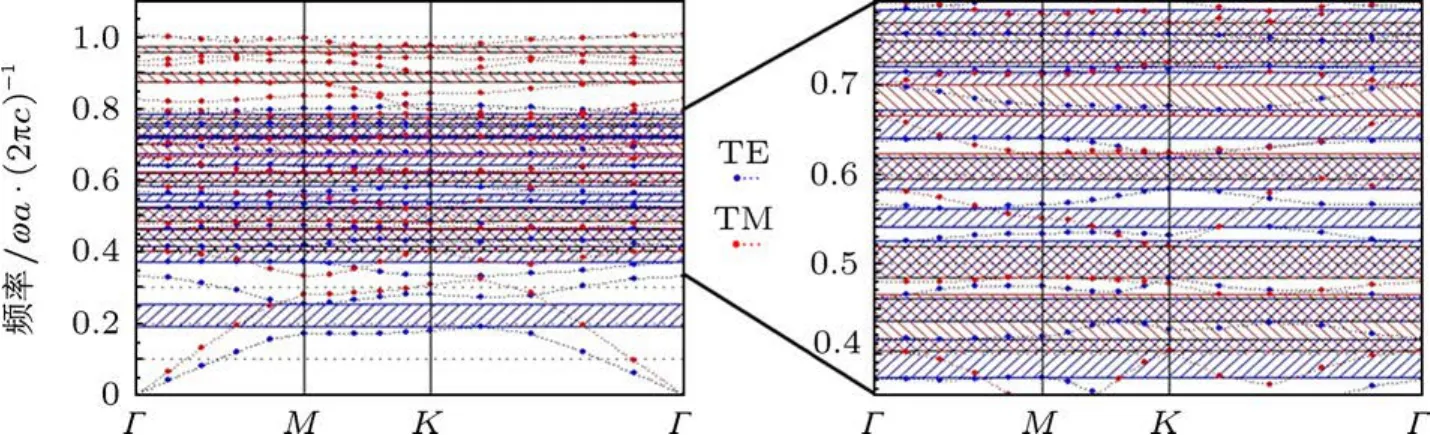
图5 ε=16,R=0.44,r=0.2R,θ=0◦时太极散射子能带结构图

4 结论

本文采用平面波展开法研究了介电常数对比度、结构参数大圆半径R、小圆半径r与大圆半径比率r/R以及旋转角度θ对太极形介质柱六角光子晶体带隙特性的影响.经过分析得知,随着介电常数对比度或介质柱填充比的增大,太极散射子完全禁带向低频方向移动;随着ε,R,r,θ的增大,完全禁带最大宽度不是随之增大,而是存在一个峰值.当ε=17,R=0.38µm,r=0.36R,θ=0◦时,获得最大完全禁带宽度0.0541(ωa/2πc).当ε=16,R=0.44,r=0.2R,θ=0◦时,光子晶体完全带隙数目最多达到8条.选择合适的参数可以使光子晶体获得更好的特性,本文研究为光子晶体结构的设计及光子晶体器件的研究提供了很好的依据.

[1]Yablonovitch E 1987 Phys.Rev.Lett.58 2059

[2]John S 1987 Phys.Rev.Lett.58 2486

[3]Ma X Y 2010 The Theory and Applications of Photonic Crystal(Vol.1)(Beijing:Higher Education Press)pp2-3(in Chinese)[马锡英2010光子晶体原理及应用(北京:科学出版社)第2-3页]

[4]Ho K M,Chan C T,Soukoulis C M 1990 Phys.Rev.Lett.65 3152

[5]Chen M Y,Yu R J 2004 Opt.Commun.235 63

[6]Yang Q Q,Hou L T 2009 Acta Phys.Sin.58 8345(in Chinese)[杨倩倩,侯蓝田2009物理学报58 8345]

[7]Russell P 2003 Appl.Phys.Rev.299 358

[8]Lou S Q,Wang Z,Ren G B,Jian S S 2004 Phys.Rev.B 13 1052

[9]Limpert J,Schmidt O,Rothhardt J,R¨oser F,T Schreiber,T¨unnermann A 2006 Opt.Express 14 2715

[10]Zhou C Z,Zhao L Y,Yuan L Z 2010 Chin.Phys.Lett.27 084203

[11]Wang C X,Xu X S,Li F,Du W,Xiong G G,Liu Y L,Chen H D 2006 Chin.Phys.Lett.23 2472

[12]Zhu G X,Yu T B,Chen S W,Shi Z,Hu S J,Lai Z Q,Liao Q H,Huang Y Z 2009 Acta Phys.Sin.58 1014(in Chinese)[朱桂新,于天宝,陈淑文,石哲,胡淑娟,赖珍荃,廖清华,黄永箴2009物理学报58 1014]

[13]Lu H,Tian H P,Li C H,Ji Y F 2009 Acta Phys.Sin.58 2049(in Chinese)[鲁辉,田慧平,李长红,纪越峰2009物理学报58 2049]

[14]Manzacca G,Paciotti D,Marchese A,Moreolo M S,Cincotti G 2007 Photonics Nanostruct.Fundam.Appl.5 164

[15]Szymanska M H,Hughes A F,Pike E R 1999 Phys.Rev.Lett.83 69

[16]David A,Benisty H,Weisbuch C 2007 J.Disp.Technol.3 133

[17]Zhang X S,Liu S,Liu Y 2008 Phys.Lett.A 372 3738

[18]Wierer J J,David A,Megens M M 2009 Nat.Photonics 3 163

建议病猪全部扑杀、无害化处理，但养殖户要求采用一定的治疗措施，减少经济损失。①对全场用溴氯宝（溴氯海因）1∶20倍稀释，每天清扫场地，消毒。连用3～5 d后，间隔1 d消毒1次。②使用头孢噻吩钠加双黄莲注射0.2 mL/kg体重，肌肉注射，1次/d，连用3～5 d。③使用核酸针剂0.1 mL/kg体重，肌肉注射，1次/d，连用3～5 d。④整群猪用猪益核酸100 g兑水100 kg，阿莫西林100 g兑水100 kg，VC粉100 g兑水100 kg，1次/d，连用3～5 d。

[19]Matioli E,Brinkley S,Kelchner K M,Nakamura S,DenBaars S,Speck J,Weisbuch C 2011 Appl.Phys.Lett.98 251112

[20]Chhajed S,Lee W,Cho J,Schubert E F,Kim J K 2011 Appl.Phys.Lett.98 071102

[21]Li L,Xie Y C,Wang Y Q,Hu X Y,Feng Z F,Cheng B Y 2003 Phys.Rev.Lett.20 1767

[22]Trifonov T,M arsal L F 2004 Phys.Rev.B 69 235112

[23]Cai X H,Zheng W H,Ma X T,Ren G,Xia J B 2005 Chin.Phys.14 2507

[24]Zhong K,Zhang H Y,Zhang Y P,Li X F,Wang P,Yao J Q 2007 Acta Phys.Sin.56 7029(in Chinese)[钟凯,张会云,张玉萍,李喜福,王鹏,姚建铨2007物理学报56 7029]

[25]Zhao M M,L¨u Y W,Yu J X 2008 Acta Phys.Sin.57 1061(in Chinese)[赵明明,吕燕伍,余家新2008物理学报57 1061]

[26]Rezaei B,Khalkhali T F,Vala A S,Kala fiM 2009 Opt.Commun.282 2861

[27]Li H P,Jiang L Y,Jia W,Qiang H X,Li X Y 2009 J.Mod.Opt.56 1220

[28]Zhang Y,Kong L,Feng Z 2010 Optoelectron.Lett.6 281

[29]Wang Y F,Wang Y S,Su X X 2011 J.Appl.Phys.110 113520

[30]Xiao S S,Shen L F,He S L 2003 Phys.Lett.A 313 132