天津软土地区地铁车站结构的三维地震响应
2013-10-29杨德健王晓鹏
杨德健,王晓鹏
(天津城建大学 土木工程学院,天津 300384)
历次大地震的震害表明,在地层可能发生较大变形和位移的部位,地铁等地下结构就可能出现严重的破坏[1].震害调查资料和研究结果[2]也表明,软土地基会增大地震作用的破坏程度.因此,对处于软土地基中的地铁车站的抗震能力进行研究,据此建立分析理论和设计方法显得十分必要.根据天津软土地区工程实例,利用大型有限元分析软件ANSYS,建立了土-结构非线性动力相互作用的三维有限元分析模型,为软土地区地铁车站的设计提供参考依据.
1 工程概况
天津地铁 5号线月牙河路站标准段为二层双柱三跨箱型结构,车站总长183.8 m,宽度24.9 m,结构总高度13.11 m,设计覆土约3.4 m.顶板厚0.9 m,中板厚0.4 m,底板厚1.0 m,侧墙厚0.9 m.车站结构的中柱采用边长为0.8 m×0.9 m的矩形柱,中柱之间沿车站纵向跨度为9.75 m,沿车站宽度方向跨度为5.5 m,中柱距墙两边距离为8.8 m.
2 基本假定与计算范围
2.1 基本假定
土体与结构相互作用问题存在着两种非线性:一种是由于土体的非弹性引起的材料非线性,本文选取Drucker-Prager本构模型来实现土体材料的非线性;另一种是由于结构与其周围土体之间产生局部脱离、滑移而造成的状态非线性,本文通过接触单元模拟土-结构相互作用的接触非线性.在进行土-地下结构地震反应分析时,计算中采用如下基本假定:
(1)土与地下结构的地震激励来自基岩面(或假想基岩面),基岩面上各点的运动一致,即不考虑行波效应;
(2)假定地震波是从基岩面垂直向上传播的剪切波和压缩波,不考虑地震斜波;
(3)采用总应力分析方法,不考虑孔隙水压变化和砂土地震液化的影响,不考虑地震引起的地基沉降和失稳.
2.2 计算范围
土体的计算范围如图1所示.
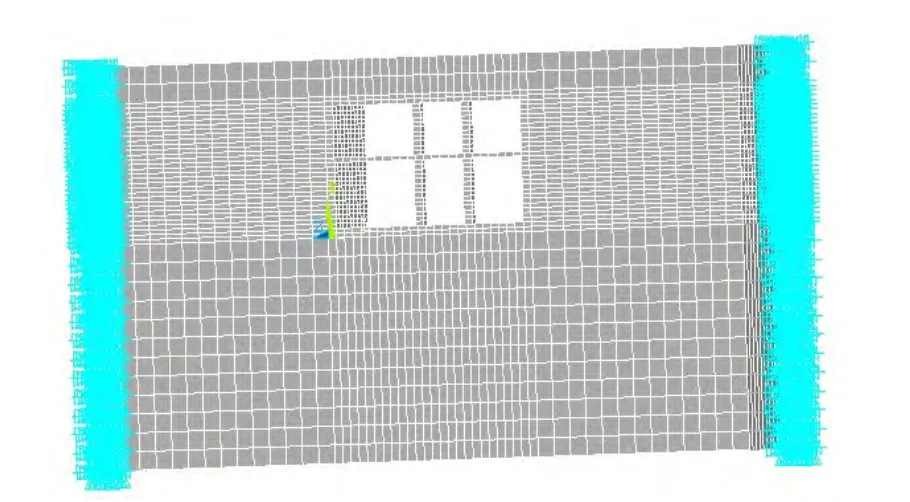
图1 土-结构整体模型
有限元的计算对象只能是有界域,因此在计算中使用人工边界来确定分析区域.由于三维模型的计算规模将随边界尺寸的增大而呈级数增加[3-4],因此,考虑到已使用人工边界来模拟地基无限域对波动能量的辐射作用,以及边界外介质的弹性恢复能力,故计算土域在结构宽度方向(X方向)上取结构宽度的 3倍.文中取地基计算宽度77 m,高度43 m,纵向长度取一个跨度9 m.
3 三维数值模型
3.1 模型参数
地铁车站模型采用ANSYS有限元分析模型,土-地铁车站结构动力相互作用体系的网格划分见图2.车站结构和周围土体统一采用三维实体单元solid45进行模拟,建模时可仅从材料性质上区别车站结构和周围地基土介质,采用combin14无质量单元模拟弹簧-阻尼效果,采用 conta173、conta174接触面单元和targe169目标面单元来模拟土-结构的非线性接触分析.
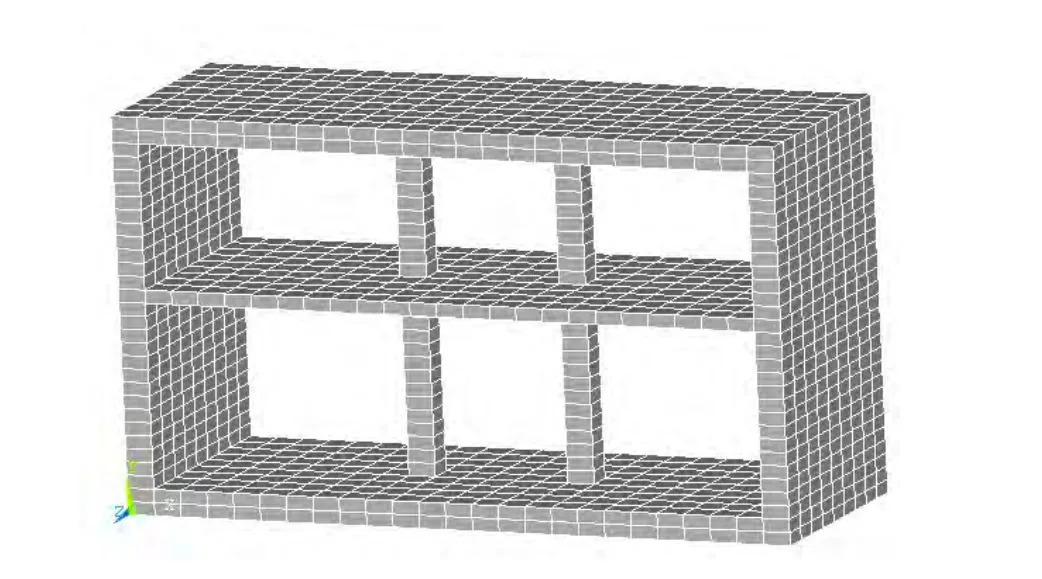
图2 车站计算模型
软土地基土的摩擦角较小,土体采用ANSYS自带的 Drucker-Prager模型近似模拟土体的塑性,调整后的土层材料参数见表 1.普通钢筋混凝土结构采用弹性模型,其阻尼比取ξ =0.05.按常规方法,混凝土材料的动力特性参数参照静弹性模量给出.研究表明:动弹性模量比静弹性模量高出30%~50%,一般取Ed=Es×140%.混凝土强度等级为 C45时,则 Ed= 3.35×104× 1.4= 4.69× 104MPa ,混凝土泊松比取0.2.
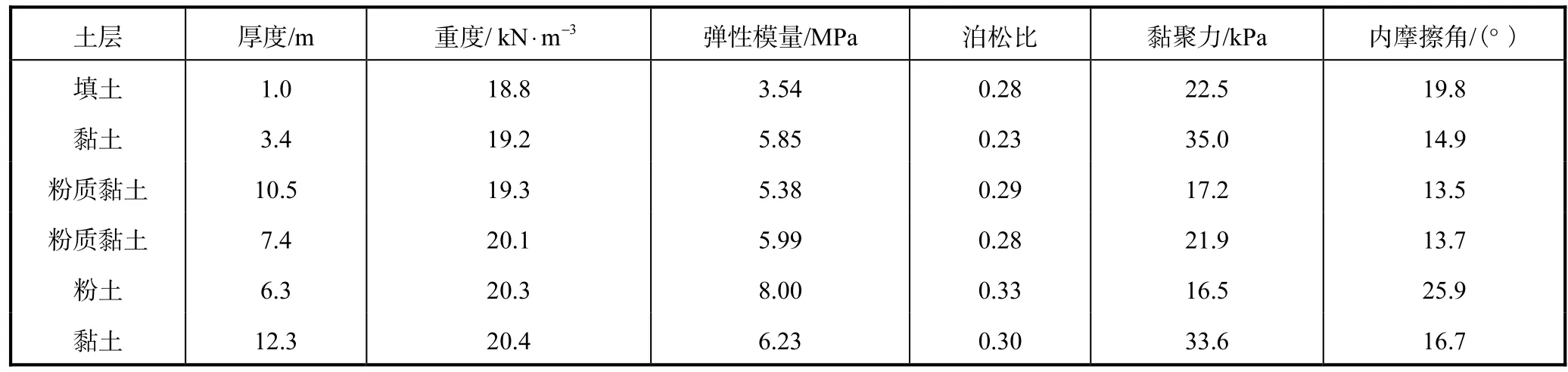
表1 场地土的材料参数
3.2 黏弹性人工边界
采用有限元分析时,只能从半无限空间选取有限土体,截断边界处无法反映边界以外土体的影响.为了减少误差,采用黏弹性人工边界,该动力边界不但可以模拟散射波由有限域向无限域的传播,同时也可模拟边界外土层介质的弹性恢复性能
根据文献[5-6],黏弹性人工边界可等效为在截断边界处设置连续分布的并联弹簧-阻尼器系统,物理元件参数如下
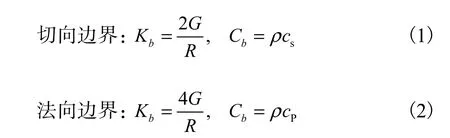
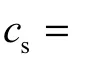
式(1)与式(2)推导时采用了柱面波假设,底部边界的平均值R取底部中点到人工边界的垂直距离,侧边界的平均值R取侧边中点到底部边界的垂直距离,在ANSYS程序中用Combine14模拟弹簧-阻尼元件,每个元件的阻尼系数和刚度系数应乘以该元件所在节点的支配面积.
模型在结构宽度方向(X方向)两侧使用了黏弹性人工边界,用以吸收散射波和模拟远场土介质的弹性恢复性能,模型底部采用水平自由、竖向约束,结构长度方向两侧和模型顶部为自由面边界.
3.3 阻尼的确定
由于Rayleigh阻尼矩阵计算方便,且节约内存,因此在本次动力分析中,采用的是Rayleigh阻尼[7].在黏滞阻尼的基本假定基础上,将整体阻尼矩阵用整体质量矩阵和整体刚度矩阵的线性组合来表示,即

利用模态分析可得到前二阶圆频率及阻尼比,从而可以从式(4)、式(5)计算得到α 及β
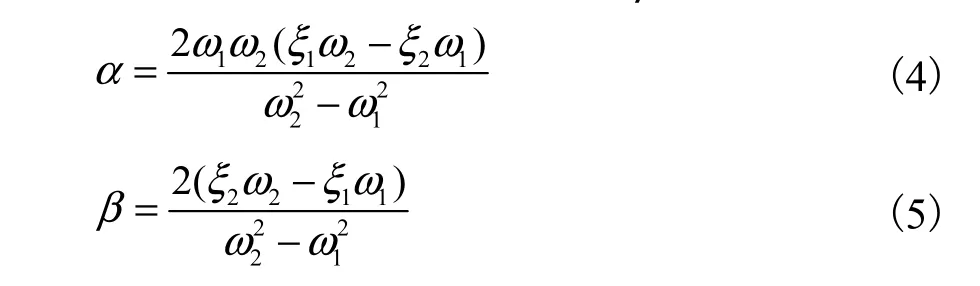
式中:ω1、ω2为多质点体系第一、第二振型的自振圆频率;ξ1、ξ2为第一、第二振型阻尼比,由实验确定.在实际工程中,一般取多质点体系的前两阶自振圆频率,阻尼比取0.05.
3.4 地震波的输入
采用天津地震波进行天津地铁车站与区间隧道地震动力响应分析.为了能够更全面地考察地铁车站在三维地震作用下的响应,对模型分别输入水平 X方向的加速度(工况一)、同时输入水平X方向和竖直Y方向加速度(工况二)两种工况.地震烈度为7度中震(0.15 g地震加速度),场地类别为三类,计算时间为19 s.水平地震波的加速度峰值为1042cm/s,竖向地震波的加速度峰值为712cm/s,如图3所示.在输入地震波的时候需乘以两个不同系数,从而调整峰值均达到0.15 g.
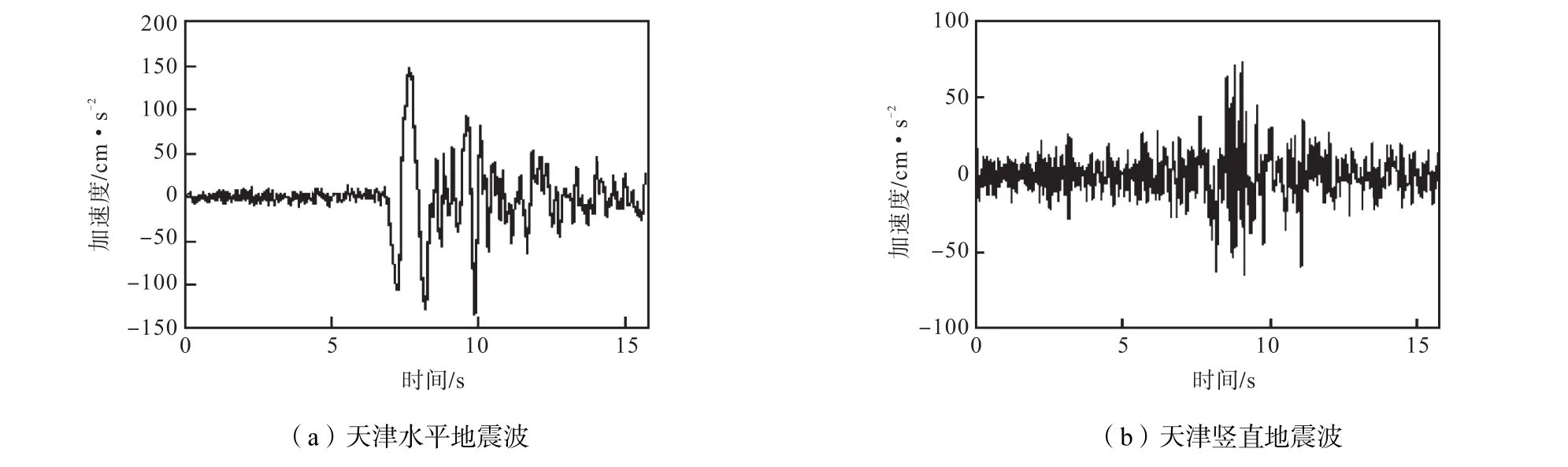
图3 天津地震波
4 数值分析结果
选取地铁车站的一个典型截面,主要考察的单元和节点编号如图 4所示.考察地震作用下结构的应力、加速度响应和地铁车站中柱的相对位移响应,进而确定结构的薄弱部位和危险发生的时刻,为抗震设计提供参考.
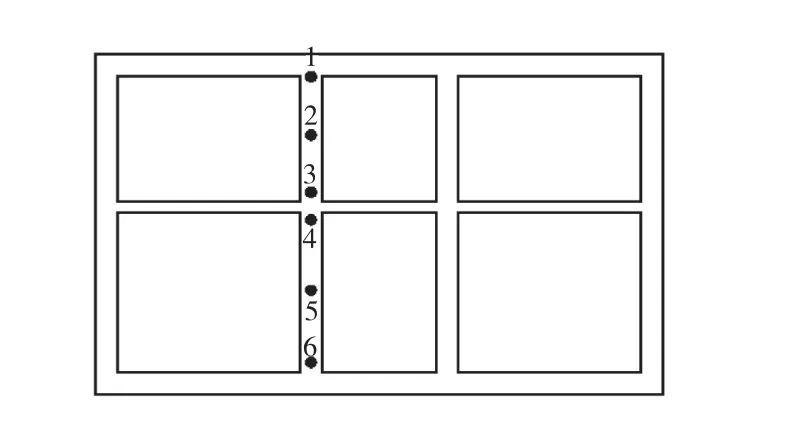
图4 结构截面节点编号
4.1 车站中柱第一主应力分析
车站结构在某一时刻的应力云图如图5所示.

图5 车站结构应力云图
下层中柱柱顶和柱底的第一主应力时程曲线如图6所示.由图6可知:在水平地震波单独作用下(工况一),地铁车站中柱产生的第一主应力最大值为770 kPa,最大第一主应力的节点为 4号节点,最大第一主应力发生的部位为下层中柱柱顶,发生最大第一主应力的时刻为7.79 s;在水平和竖直地震波共同作用下(工况二),中柱产生的第一主应力最大值为1281 kPa,最大第一主应力的节点为1号节点,最大第一主应力发生的部位为上层中柱柱顶,发生最大等效应力的时刻为9.09 s.通过分析两种工况下中柱各点的最大主应力,可知中柱与顶板、底板和中板的连接处为地铁车站的薄弱部位,第一主应力主要由水平地震波控制,但竖直地震波的作用同样不可忽视.
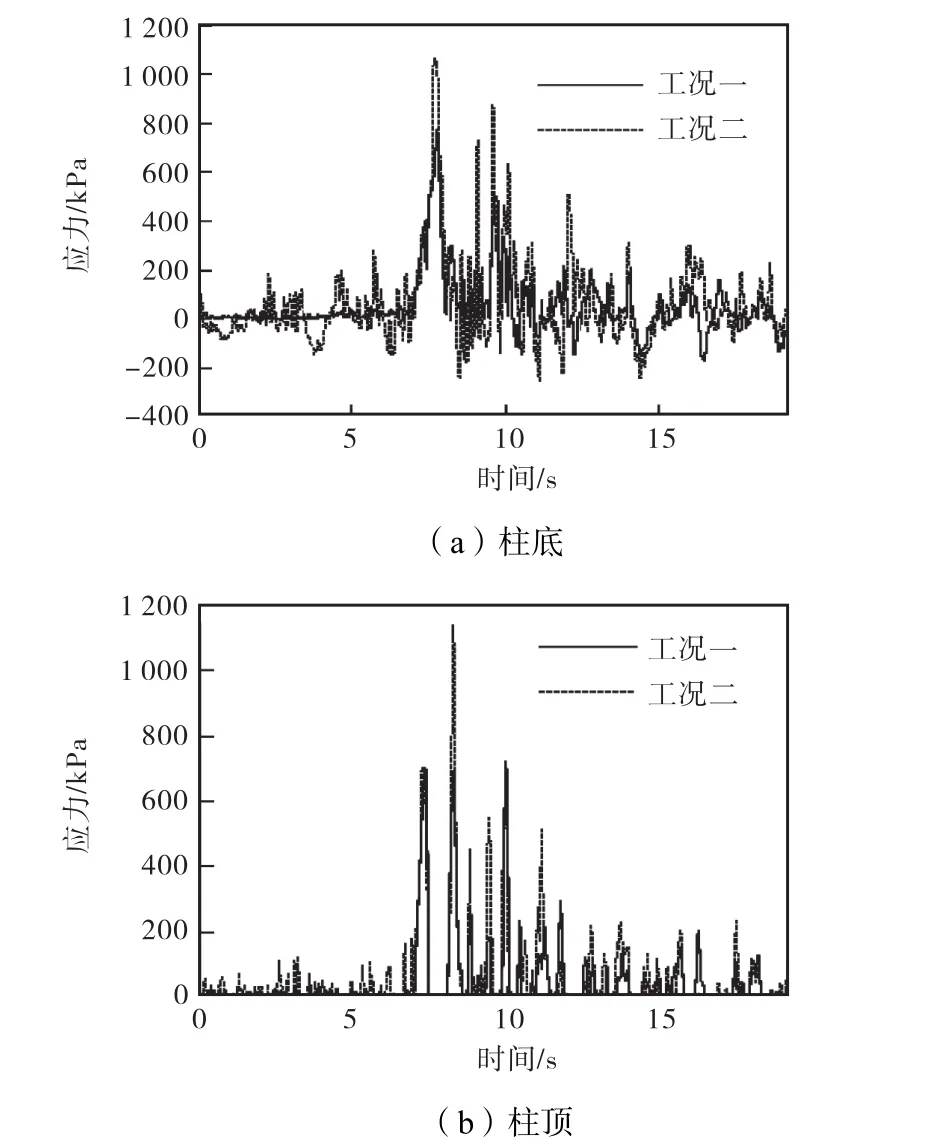
图6 下层中柱第一主应力时程曲线
结构截面各节点产生的第一主应力最大值如表2所示.

表2 第一主应力最大值 kPa
4.2 下层中柱水平相对变形
中柱的水平相对位移是地铁车站地震响应评价分析中的一个重要方面,其中下层中柱的表现尤为突出.在两种工况下,下层中柱柱顶和柱底的水平相对位移时程曲线如图7所示.由图7可知:水平地震波单独作用时(工况一),中柱的水平相对位移在7.38 s达到最大值 4.27 cm,下层中柱的层间位移角为1/164;水平和竖直地震波共同作用时(工况二),中柱的水平相对位移在7.38 s达到最大值4.38 cm,下层中柱的层间位移角为1/160.两种工况下中柱的变形几乎相等,可见,中柱的水平相对位移主要由水平地震波控制,竖直地震波的作用可以忽略.
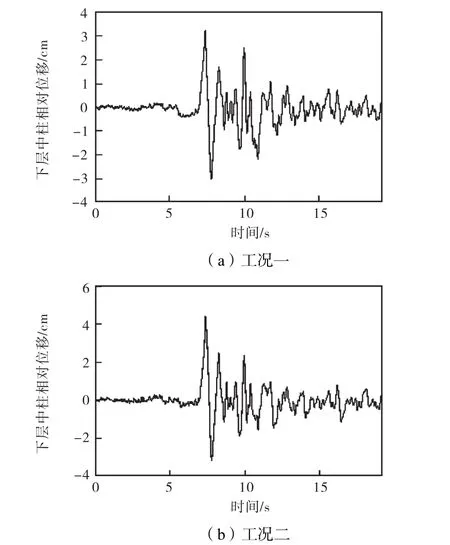
图7 下层中柱水平相对位移时程曲线
4.3 中柱的加速度时程反应
在两种工况下,下层中柱的柱顶和柱底的水平、竖直方向加速度反应时程曲线如图8、图9所示.由图 8-9可知:对于水平方向加速度反应,在时程曲线的前区段和后区段,柱顶的加速度反应比柱底稍大;在时程曲线的中区段,柱顶的加速度反应明显大于柱底的加速度反应.对于竖直方向加速度反应,在整个地震过程中,柱顶和柱底的加速度反应差别不大.分析图8中的两组时程曲线可知,水平方向的加速度反应由水平地震波控制,竖直地震波的影响可以忽略.
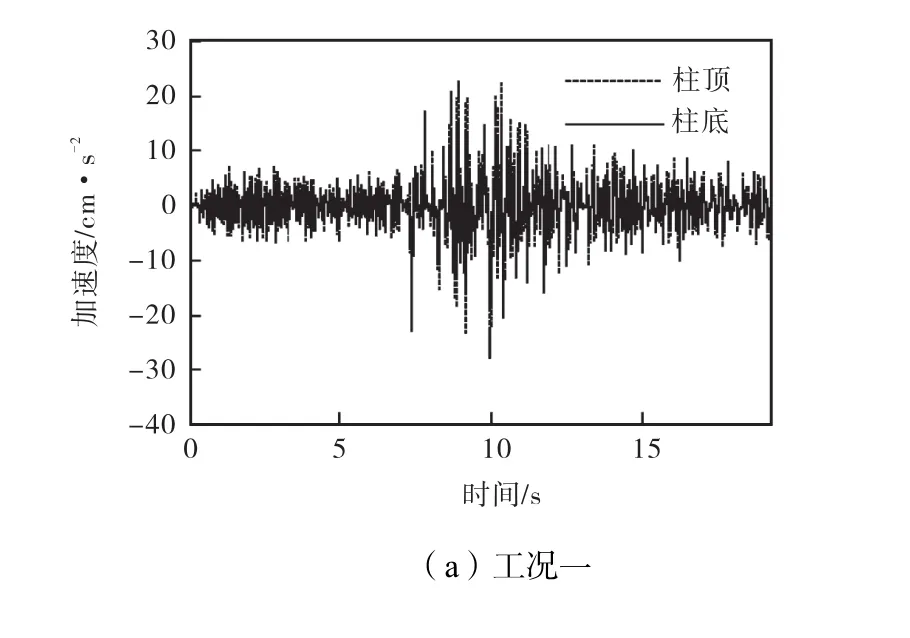
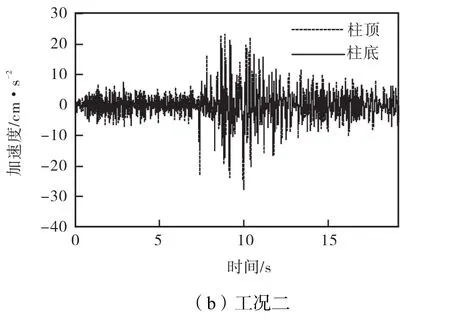
图8 水平方向加速度反应时程曲线
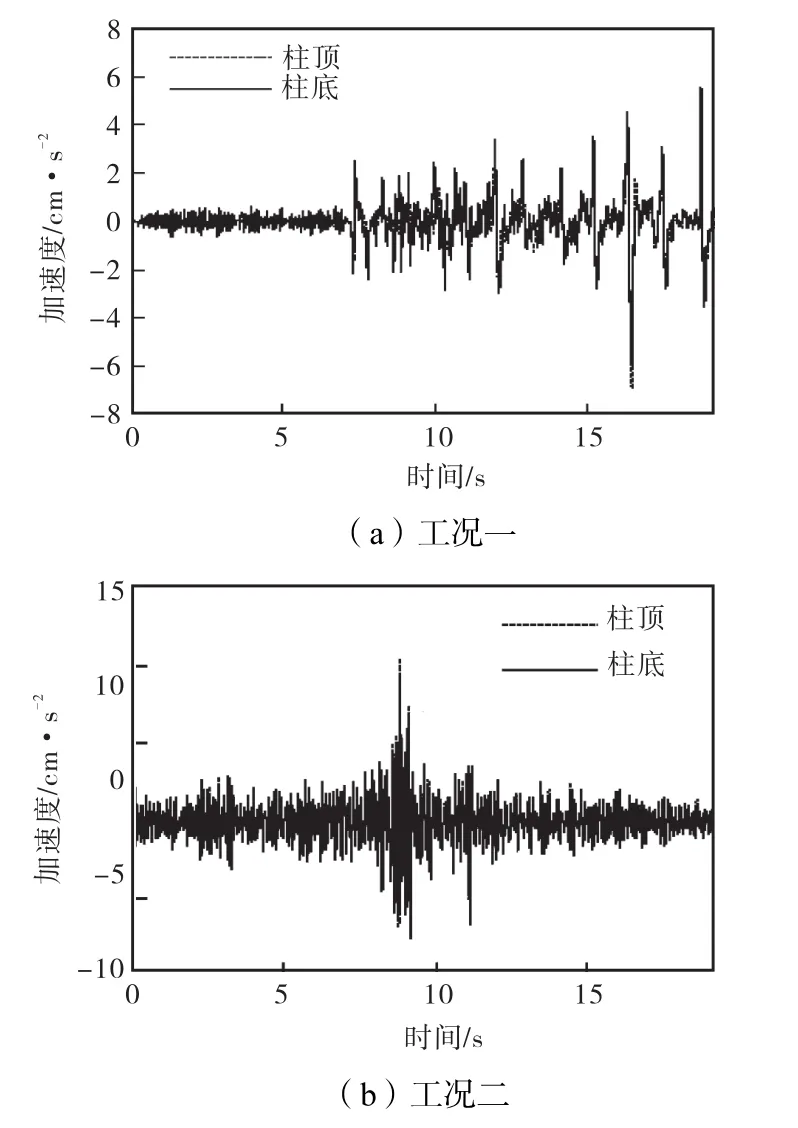
图9 竖直方向加速度反应时程曲线
5 结 论
(1)中柱与顶板、底板和中板的连接处为地铁车站的薄弱部位,第一主应力的产生主要由水平地震波控制,但竖直地震波的作用同样不可忽视.
(2)地铁车站中下层中柱柱顶和柱底的相对位移是地震响应评价分析的重要方面.在水平和竖直地震波共同作用时,下层中柱的层间位移角可达1/160;中柱的水平相对位移主要由水平地震波控制,竖直地震波的作用可以忽略.
(3)柱顶和柱底的水平方向加速度响应在地震过程的中段相差较大;柱顶和柱底竖直方向的加速度响应在整个地震过程中的差异可忽略;水平方向加速度反应主要由水平地震波控制.
[1]曹炳政,罗奇峰,刘晶波,等. 神户大开地铁车站的地震反应分析[J]. 地震工程与工程振动,2002,20(4):102-107.
[2]黄 雨,叶为民,唐益群,等. 上海软土场地的地震反应特征分析[J]. 地下空间与工程学报,2005,1(5):773-778.
[3]袁 蕾,姜忻良. 地铁换乘站不规则结构对其地震响应的影响[J]. 地震工程与工程振动,2011,31(1):74-79.
[4]庄海洋,宰金珉,陈国兴. 土-地下结构的非线性动力相互作用——理论及应用[J]. 自然灾害学报,2006,15(6):174-181.
[5]谷 音,刘晶波,杜义欣. 三维一致粘弹性人工边界及等效粘弹性边界单元[J]. 工程力学,2007,24(12):31-37.
[6]刘晶波,王振宇,杜修力,等. 波动问题中的三维时域黏弹性人工边界[J]. 工程力学,2005,22(6):46-51.
[7]曾佳亮. 富水软土地铁车站压顶梁抗震设计探讨[J].铁道标准设计,2012(9):81-85.
