基于运动矢量时—空特性的快速运动估计算法研究

刘龙，宋琦军，赵太飞，元向辉

(1. 西安理工大学 自动化学院，陕西 西安710048；2. 西安交通大学 电信学院，陕西 西安 710049；3. 中国电子设备系统工程公司，北京100091)

1 引言

基于块匹配的运动估计是视频压缩编码中的必要环节。迄今为止，不同的国际视频压缩编码标准均采用了块匹配（BMA）算法进行运动估计，如H.261、H.263、MPEG-1、MPEG-2、MPEG-4 和H.264等编码标准。大量的数据测试表明，运动估计的运算量非常大，以至于影响视频编码的实时性能，快速有效的运动估计算法对于高质量视频编码具有重要意义。

目前，基于块匹配的快速运动估计算法涉及了搜索模式、初始搜索点预测、自适应机制等方法。搜索模式的设计思路是尽可能根据运动矢量分布的特点设计合理匹配点阵形状，从而减少搜索收敛前的搜索点数；初始搜索点的预测是使得搜索范围尽可能接近最终收敛点从而减少运算量；自适应技术主要是根据视频信息进行一定分析并对运动估计进行分类，根据不同类别采用不同的搜索模式，这样能够起到一定的优化运算，从而提高了运算速度。目前，主流的运动估计算法是上述3种方法的综合实现。

典型的搜索模式算法包括三步法[1]（TSS）、四步法[2](FSS)和钻石法[3](DS)等，其中，钻石法最为成功，被MPEG-4标准所采纳。Tourapis A M等人在文献[4]中首次引入了对初始搜索位置的预测；在文献[5]中，Nisar H等人将时间信息分别表示为MVTR(n - 1 )、 M VTB(n -1)、 M Vp( n- 1 )，空间信息分别表示为 M VSL(n)、 M VSA(n)，采用了时间和空间信息的均值或中值进行预测，Lin Zhaohua[6]等人定义了局部运动程度(LMA, local motion activity)来衡量当前宏块与相邻宏块的运动一致性程度，LMA被分为低程度（ L ≤L1）、中等程度(L1＜L≤ L2)和高程度（ L ＞L2），当LMA为低程度时，搜索策略选取空间预测器初始化搜索中心起始点的位置，当LMA为中等或高程度时，搜索策略选取空间和时间预测器中 SAD值最小的为搜索中心的起始点。随着快速运动估计算法的发展，一些新的算法提出了自适应选择搜索模式的机制，Hosur P I[7]和 Tourapis A M[4]等人首现提出了自适应搜索算法MVFAST和PMVFAST，采用空间上邻近被预测运动矢量的3个运动矢量中最大的运动矢量与某个阈值比较进行矢量分类，并根据不同的运动矢量分类选择不同的搜索模式；Ahmad I[8]等人根据运动矢量大小判断视频信号在时—空间上运动剧烈程度；Lin Zhaohua[9]和ChenXiaolin等[10]则通过统计分析相邻运动矢量预测运动的剧烈程度，并根据运动的剧烈程度调整搜索的范围，根据不同的推断自适应地选择不同的搜索模式的方式提高运动估计的速度，方法本质与文献[8]类似。Lee Sangkeun[11]首先对视频场景的内容进行了分析，并自适应调整给定的搜索范围； Paramkusam等[12]根据相邻帧像素块的差值预测初始搜搜位置减少计算时间；Zaynab Ahmed等[13]根据空间相邻的运动矢量的均值预测当前与估算运动矢量的大小，并根据预测结果采用动态十字搜索模式进行运动估计。另外，赵志杰等人[14]针对多视角视频编码中的运动估计问题，利用帧间、视角间相关性，建立预测矢量状态集合，通过马尔科夫链模型的状态转移概率，对预测矢量进行提前测试，然后利用提前退出准则，实现快速运动矢量估计。谷会涛等人[15]提出了一种基于多搜索中心预测和搜索范围动态调整的快速算法，对当前宏块时间和空间上相邻块的运动向量进行分析, 得出多个预测向量作为运动估计的搜索中心，降低了运动估计的运算量。

综上所述，视频快速运动估计算法设计关键在于能否建立合理的预测方法，并设计相应的搜索模式。现有的算法都不同程度的依赖了空间或时间信息对待估计运动矢量进行预测，同时采用自适应选择搜索模式已达到尽可能快速收敛从而提高估计速度的目的，但值得指出的是实际上很多的视频序列会出现较复杂运动场景，这时空间和时间上的视频信号相关性较弱，往往运动特征会出现突变，使得预测产生很大的误差，仅依据运动矢量大小、视频内容以及统计分析来对待估计运动矢量进行分类显然是不充分的，应该看到运动矢量在时—空上的可预测性与其在时间和空间上的分布和变化规律是紧密联系的，如不能很好的根据运动矢量在时间和空间上的特点进行分类处理，那么在运动复杂的情况下不仅不能提高估计速度反而会使估计速度下降。本文将重点研究如何根据运动矢量时—空特性建立更加合理有效的预测自适应机制，提出了一种新的基于空间运动相似性的运动矢量预测自适应机制，并将其应用到快速运动估计算法中提高运动估计的速度，克服现有算法的不足。

2 运动矢量时—空特性分析

运动矢量预测的准确性直接受到其时—空相关性的影响，相关性程度高，预测的准确性高；反之，预测的准确性低。本节将从运动矢量相关性程度的角度对运动矢量的时—空特性进行分析，并给出运动矢量在时间上的变化程度与空间上相似度之间的关系。

2.1 特性分析

在时间维度上，运动矢量的变化程度直接反映了运动矢量在时间上的相关性程度，在相邻时间点上变化程度越大，相关性越弱；反之，相关性越强。为了分析运动矢量在时间上的相关性特点，首先定义运动矢量的变化程度如下。

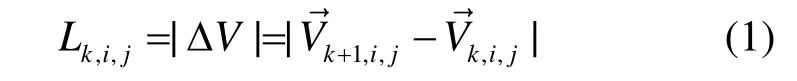
表 1显示了运动矢量在时间上变化的统计数据。统计数据结果显示大多数的运动矢量在连续 2个运动矢量场之间不变化或变化很小。经过计算，对于运动复杂度低的视频序列，超过70%的运动矢量没有明显的变化；超过90%的运动矢量变化幅度小于3个单位像素；变化幅度超过3个单位的运动矢量很少；对于运动复杂度高的视频序列，有30%左右的运动矢量没有明显的变化；超过60%的运动矢量变化幅度大于3个单位像素，从上述数据中可以看出，对于运动复杂程度不同的视频序列，运动矢量在时间轴上有的相关性弱，这表明在该情况下，时间上的可预测性具有不稳定性。综上所述，可以得到以下结论：在视频运动复杂程度高时，运动矢量在时间上的变化剧烈，由此导致了在时间上的可预测性的降低；相反地，在视频运动复杂程度低时，运动矢量在时间上的变化平缓，运动矢量在时间上的可预测性增高。

表1 运动矢量在时间上的变化统计/像素

在空间上，局部区域的相似性程度直接反映了运动的复杂程度与空间相关性程度，相似度越差，运动复杂程度越高，相关性程度越低；反之，运动复杂程度越低，相关性程度越高。本文采用局部区域运动矢量的方差来描述空间运动的相似度。假定MBk,i,j是k帧中坐标为(i, j)的宏块，i和 j分别表示宏块的横纵坐标； Rk,i,j表示包含宏块 M Bk,i,j及其相邻宏块的集合；Sk,i,j表示集合 Rk,i,j中所有宏块所对应的运动矢量形成的集合。定义集和 Sk,i,j的均值和方差如下

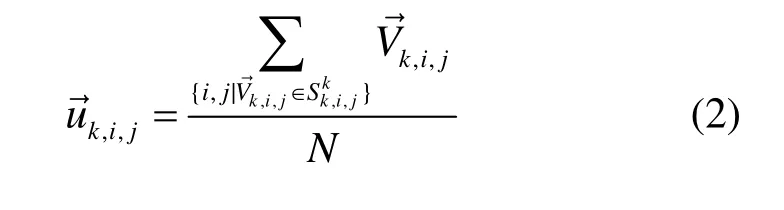
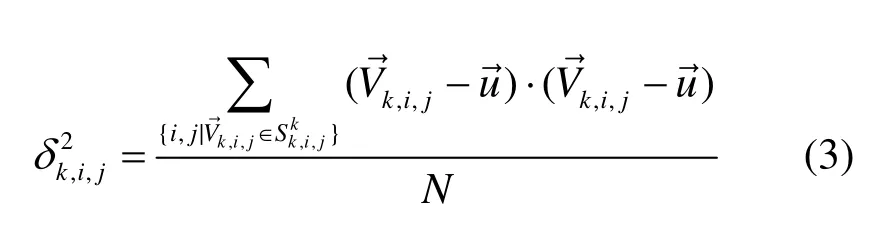
其中， Rk,i,j包含了 M Bk,i,j及其相邻的8个宏块。

综上所述，可以得到以下结论：在视频复杂程度高的局部区域，运动矢量在空间上的相似度较差，相关性程度低；相反地，在视频运动复杂程度低的局部区域，运动矢量在空间上的相似度较高，相关性程度高。

2.2 运动矢量的时空特性

运动矢量的空间特性与时间特性存在一定的关系，也可以说局部区域运动矢量的变化程度和相似度之间存在着某种关系。在运动复杂度高的区域，运动矢量的局部区域相似度较低，其时间上的变化程度也会较大；而在运动复杂度低的区域，运动矢量的局部区域相似程度较高，其时间上的变化程度也会较小。本文对 20视频序列计算和Lk,i,j值，绘制其在二维坐标系中，局部运动相关性程度和运动矢量的变化程度可以近似的看作线性关系。图 1显示了视频序列 Foreman、Flower Garden、Stefan和Hall monitor的结果。本文采用线性模型描述运动矢量的变化程度和相似度之间的关系可表示为

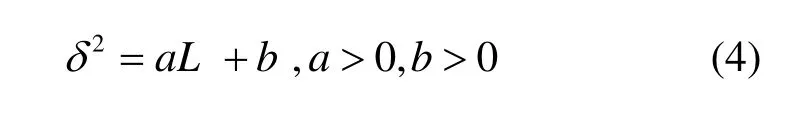
图1 2δ和L的关系

3 本文提出的快速运动估计算法

3.1 运动矢量的分类

根据2.1节的分析，可根据L值与阈值进行比较将运动矢量分为3种类型，即不可预测运动矢量（NPMV, no predictable motion vector）、中度可预测运动矢量（MPMV, medial predictable motion vector）和高度可预测运动矢量（HPMV, high predictable motion vector）。设定运动矢量的分类阈值为L T= ，运动矢量可以被分为 3类：无变化的运动矢量(0L=)；小变化运动矢量（0LT＜≤）；大变化运动矢量(LT＞)。分类过程可以定义为

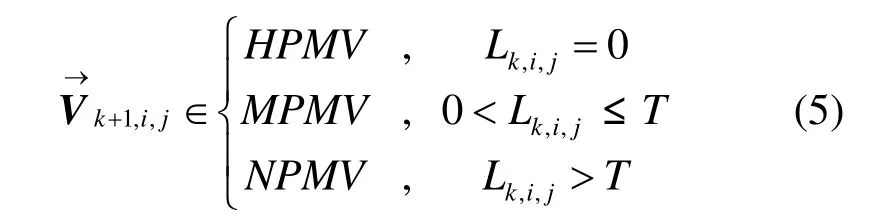
根据式(4)和式(5)可以被转换成下述等式

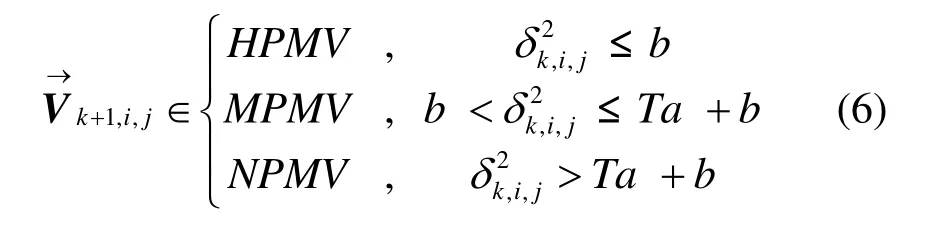
3.2 如何计算系数a和b

式（6）中的系数a和b对于不同的视频有不同的值。在运动估计的初始阶段，式（6）中的系数a和b首先被初始化。采用全搜索法估计两帧运动矢量场。通过最小二乘法计算系数a和b，其过程描述如下。

假定运动矢量场中有N个运动矢量；通过式(1)和式(3)计算

预测误差为

则平方误差如下

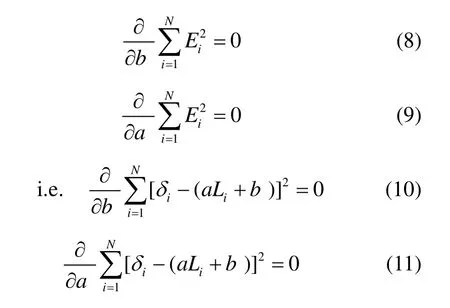
最终的计算式如下

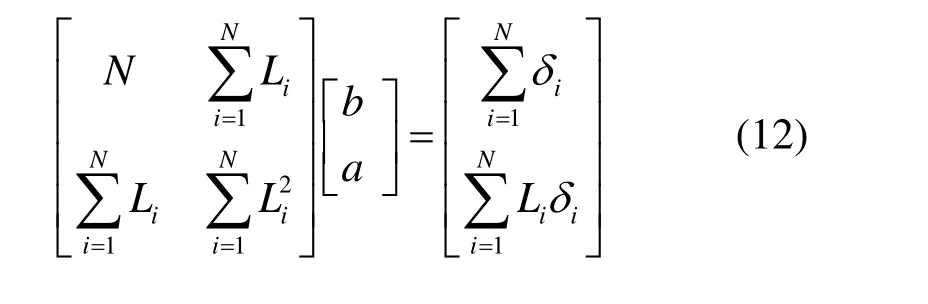
3.3 搜索模式

根据3.1节的运动矢量分类，本文提出了小钻石模式（SDSP）和方形模式（SSP），如图2所示。

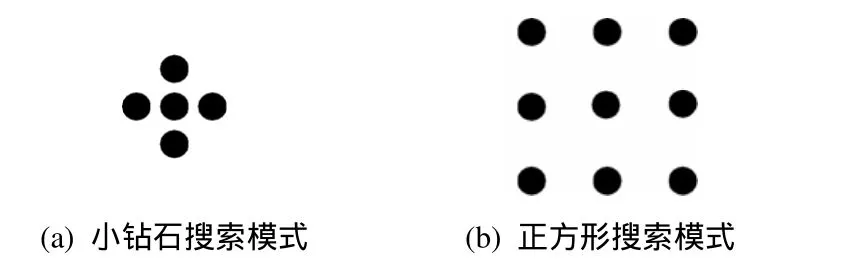
图2 搜索模式

1) 小钻石搜索策略

步骤1 初始化搜索中心位置；

步骤2 对SDSP的5个点进行像素块失真计算。如果最小失真值出现在中心点，那么进行步骤4；如果最小失真值没有出现在中心点，则进行步骤3；

步骤 3 以上一步骤中最小的失真值点为中心进行新的SDSP搜索计算。如果最小失真值出现在中心点，那么进行步骤 4；如果最小失真值没有出现在中心点，则重复该步骤；

步骤 4 以上一步骤中最小的失真值点为终止搜索点计算运动矢量。

2) 方形搜索策略

步骤1 初始化搜索中心位置；

步骤2 对SSP的9个点进行像素块失真计算；

步骤 3 以上一步骤中最小的失真值点为中心进行SDSP搜索计算。如果最小失真值出现在中心点，那么进行步骤 5，如果最小失真值没有出现在中心点，则进行步骤4；

步骤 4 以上一步骤中最小的失真值点为中心进行新的SDSP搜索计算。如果最小失真值出现在中心点，那么进行步骤 5；如果最小失真值没有出现在中心点，则重复该步骤；

步骤 5 以上一步骤中最小的失真值点为终止搜索点计算运动矢量。

3.4 快速运动估计算法

本文提出的运动估计算法分为3个步骤。假定在运动估计的次序是从左到右、从上到下并且k帧的运动矢量是已知的。对 k + 1帧运动矢量场进行估计，估计过程如下：1→) 系 数a和b进行初始化计算；2) 通过式（6）对进行分类; 3) 根据不同的分类结果，采用不同的搜索策略对进行估计。当 属于不可预测，用中心位置点作为搜索初始点，采用钻石搜索法对进行估计；当→ 属于中度可预测，用作为搜索初始点，采用方形搜索策略对 进行估计；当 属于高度可预测，用作为搜索初始点，采用小钻石搜索策略对 进行估计。

4 实验分析

本节将对运动估计算法性能作测试，并且与FS、NTSS、DS、MVFAST[4],PMVFAST[7]和文献[8~10]、文献[11]、文献[12]、文献[13]的算法进行比较分析。在实验中，采用每帧的灰度计算运动矢量。宏块大小为16 16×。采用峰值信噪比（PSNR）衡量运动估计的精度，运动加速（speed up）来衡量运动估计的速度。实验平台选择MPEG-4校验模型编码软件。采用 TM5码率控制方案，编码比特率为500kbit/s、每秒15帧。帧间编码模式为IPPP…。

实验选取2个简单运动序列和多个复杂运动序列进行测试。本文采用 Hall Monitor、Mother &Daughter、Coastguard、Foreman、Table Tennis、Flower Garden，Stefan等7个视频序列作测试。其中，简单运动序列为Hall monitor和Mother & Daughter和Coastguard，视频场景静止或运动缓慢，目标运动缓慢；复杂运动序列为 Foreman、Table Tennis、Flower Garden和Stefan，其中，Table Tennis和Stefan属于局部运动场景，目标运动剧烈，Flower Garden和Foreman属于全局运动场景，场景复杂并伴随镜头快速移动，目标有较强烈运动。

表 2显示了测试结果。对于视频序列 Hall monitor、Mother&Daughter和 Coastguard，由于运动缓慢，运动矢量在时—空上具有较强的相关性，预测比较准确，匹配过程收敛一般较快，但在运动目标边缘或内部部分区域会出现运动的不一致性，会导致预测失败，损失估计时间，因此文献[8~13]和本文算法都有相当的速度提升，但本文算法略有优势,运动估计的精度方面基本相当。对于视频序列Foreman、Table Tennis、Flower Garden、Stefan，其中，Table Tennis和Stefan由于目标运动剧烈，目标区域运动矢量相关性弱，无法准确预测，对提升运算速度有负面影响；而对 Foreman和Flower Garden，运动场景较为复杂，预测受到很大影响，因此文献[8~13]对于速度提升并不明显，而本文算法由于对运动矢量的预测性进行了分类处理，避免了错误预测，从而在复杂场景的运动估算中具有明显的速度优势，在估计精度上略优于其他算法。

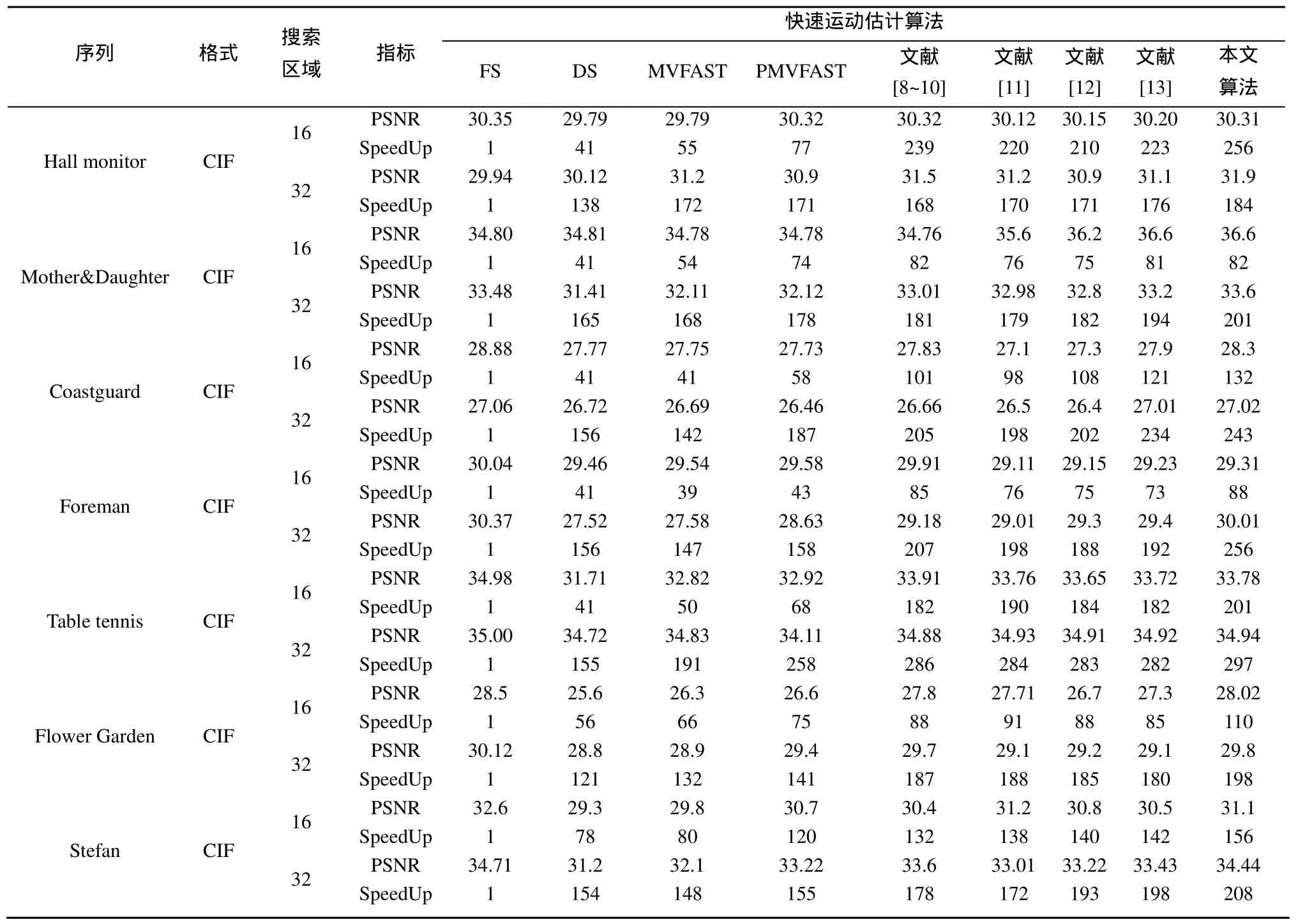
表2 运动估计算法的PSNR测试值比较

综上所述，在复杂运动场景下本文提出的算法的合理性保证了不必要匹配点的减少和搜索方向的正确性，有效地克服了其他算法在复杂运动场景下的不足，在估计精度上与其他算法相当，充分体现本文算法在提升运动估计速度方面的优势。

表 2显示了测试结果。对于视频序列 Hall monitor、Mother&Daughter和 Coastguard，由于运动缓慢，运动矢量在时—空上具有较强的相关性，预测比较准确，匹配过程收敛一般较快，但在运动目标边缘或内部部分区域会出现运动的不一致性，会导致预测失败，损失估计时间，因此文献[8~13]和本文算法都有相当的速度提升，但本文算法略有优势,运动估计的精度方面基本相当。对于视频序列Foreman、Table Tennis、Flower Garden、Stefan，其中，Table Tennis和Stefan由于目标运动剧烈，目标区域运动矢量相关性弱，无法准确预测，对提升运算速度有负面影响；而对Foreman和 Flower Garden，运动场景较为复杂，预测受到很大影响，因此文献[8~13]对于速度提升并不明显，而本文算法由于对运动矢量的预测性进行了分类处理，避免了错误预测，从而在复杂场景的运动估算中具有明显的速度优势，在估计精度上略优于其他算法。

综上所述，在复杂运动场景下本文提出算法的合理性保证了不必要匹配点的减少和搜索方向的正确性，有效地克服了其他算法在复杂运动场景下的不足，在估计精度上与其他算法相当，充分体现本文算法在提升运动估计速度方面的优势。

5 结束语

本文通过对运动矢量时—空特性的分析，建立了运动矢量在时—空变化的关系，根据这一关系，并对待估计运动矢量进行分类，采用不同的搜索模式进行快速运动估计。实验结果表明：本文提出的算法克服了其他相关算法的不足，在各种视频序列测试下明显提高了运动估计的速度并且具有与其他运动估计算法近似或更好的性能，证明了本文算法的有效性。

[1] LI R, ZENG B, LIOU M L. A new three-step search algorithm for block motion estimation[J]. IEEE Transactions on Circuits and Systems for Video Technology, 1994, 4(4):438-442.

[2] PO L M, MA W C. A novel four-step search algorithm for fast block motion estimation[J]. IEEE Transactions on Circuits and Systems for Video Technology, 1996, 6(5):313-317.

[3] THAM J Y, RANGANATH S, RANGANATH M. A novel unrestricted center biased diamond search algorithm for block motion estimation[J].IEEE Transactions on Circuits and Systems for Video Technology,1998, 8(4):369-377.

[4] TOURAPIS A M, AU O C, LIOU M L. Fast Block Matching Motion Estimation Using Predictive Motion Vector Field Adaptive Search Technique (PMVFAST)[S]. ISO/IEC/JTC12 SC29/WG11 MPEG2000/M5866, 2000.

[5] NISAR H, CHOI T S. Fast motion estimation algorithm based on spatio-temporal correlation and direction of motion vector[J]. Electronics Letters, 2006, 42(24):1384-1385.

[6] LIN Z H, ZOU Y B. A novel fast motion estimation algorithm based on starting search point prediction[A]. 2009 Internation Coference on Measuring Technology Mechatronics Automation[C]. Changsha,China, 2009.746-749.

[7] HOSUR P I, MA K K. Motion vector field adaptive fast motion estimation[A]. Second International Conference On Information, Communications and Signal Processing (ICICS’99)[C]. Singapore, 1999. 7-10.

[8] AHMAD I, ZHENG W G, LUO J C. A fast adaptive motion estimation algorithm[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2006, 16(2):420-427.

[9] SOROUSHMEHR S M R, SAMAVI S, SHIRANI S. Fast block motion estimation based on sorting of prediction vectors[J]. Canadian Journal of Electrical and Computer Engineering, 2010, 35(1):25-32.

[10] CHEN X L, CANAGARAJAH N S, JOSE L N Y. Backward adaptive pixel-based fast predictive motion estimation[J]. IEEE Signal Processing Letters, 2009, 16(5):370-373.

[11] LEE S K. Fast motion estimation based on adaptive search range adjustment and matching error prediction[J]. IEEE Transactions on Consumer Electronics, 2009, 55(2):805-811.

[12] PARAMKUSAM A V, REDDY V S K. New fast motion estimation algorithm in video coding[A]. 2011 IEEE Recent Advances in Intelligent Computational Systems (RAICS)[C]. India, 2011. 441-446.

[13] AHMED Z, HUSSAIN A J, AL-JUMEILY D. Mean predictive block matching(MPBM) for fast block matching motion estimation[A]. 2011 3rd European Workshop on Visual Information Processing (EUVIP)[C].Paris, France, 2011. 67-72.

[14] 赵志杰，范智鹏，金雪松等. 针对多视角视频编码的快速运动估计方法[J]. 通信学报, 2011. 32(10):152-157.ZHAO Z J, FAN Z P, JIN X S, et al. Fast motion estimation in multi-view video coding[J]. Journal on Communications, 2011, 32(10):152-157.

[15] 谷会涛, 陈书明, 孙书为等.多搜索中心的运动估计快速算法[J].电子学报. 2011, 39(3):695-699.GU H T, CHEN S M, SUN S W, et al. Fast motion estimation algorithm based on multi-search centers[J]. Acta Electronica Sinica, 2011,39(3): 152-157.