基于自适应势函数塑造奖赏机制的梯度下降Sarsa(λ)算法

肖飞，刘全,2，傅启明，孙洪坤，高龙

（1．苏州大学 计算机科学与技术学院，江苏 苏州 215006；2．吉林大学 符号计算与知识工程教育部重点实验室，吉林 长春 130012）

1 引言

强化学习中 Agent通过试错(trail-and-error)与环境进行交互。通过时间信度分配(temporal credit assignment)机制将每个时间步获得的延迟回报(delayed reward)传递给过去动作序列中的某些动作。用值函数评价每个状态或状态动作对的好坏程度，最终通过值函数确定到达目标的最优策略。强化学习的自学习和在线学习的特性决定了其非常适用于解决复杂的、环境模型未知的、不确定的时序决策优化问题[1]。随着强化学习理论研究的不断深入，强化学习方法被越来越多地用于制造过程优化、机器人控制、游戏等领域[1～3]。

传统的强化学习方法利用二维表存储值函数，并不断进行修改，直至值函数收敛。每一个表项是状态或状态动作对及对应的估计值。这种方法清晰简单，非常适用于离散的小状态空间问题。但当处理大状态或连续状态空间问题时，会面临收敛速度慢甚至无法收敛，即“维数灾”问题[1]。解决强化学习“维数灾”问题主要有3种途径。1) 通过聚类等方法对状态空间进行离散化并降维，再利用传统的表格式强化学习方法解决问题[4]。然而在离散化操作中，如果离散化的精度太高，那么状态数会以指数级的速度增长，增加了时间和空间复杂度。如果离散化的精度太低，又无法保证所估计值函数的精度。因此该方法面临离散化精度和状态空间复杂度的权衡问题，而且离散化后无法保证收敛到原问题的全局最优解。2) 基于任务分解的思想，采用分层和并行等技术来改进强化学习方法，充分利用抽象化思想和计算资源来解决强化学习问题[5,6]。如何进行任务分解及并行方法中多个Agent间如何协作等是该类方法的难点。3) 将强化学习与函数逼近相结合，利用一个近似函数来对强化学习中的值函数进行建模，通过样本逼近真实的值函数模型[7,8]。在结合函数逼近的强化学习方法中，学习的经验信息能够从状态空间的子集泛化至整个状态空间。Agent利用近似函数选择每个状态下的最优动作。

早在20世纪90年代，Tsitsiklis及Sutton等人就对结合函数逼近的强化学习方法进行了探索和研究[9,10]。近年来，利用函数逼近来解决强化学习的“维数灾”问题已经逐渐成为了研究的热点。2009年，Bonarini等人基于模糊逻辑提出了一种模糊Q学习算法，并在模糊推理系统中验证了算法的有效性[11]。Heinen等人于2010年提出利用增量式概率神经网络来逼近强化学习问题的值函数，通过实验验证了算法的性能[12]。Maei等人于2010年提出了结合资格迹(eligibility trace)的 GQ(λ)(general Q(λ))算法，能够很好地实现时间差分(TD, temporal difference)预测学习[13]。同年，Maei 等人将 GQ(λ)算法中的目标策略设为贪心策略，λ设为0，提出了离策略Greedy-GQ算法，用于解决强化学习的控制问题，并通过Baird反例验证了算法的有效性[14]。函数逼近可以有效提高学习算法的泛化能力，对连续状态空间问题适应性很强。然而，强化学习方法通过反向传播延迟回报机制来解决时间信度分配问题，TD学习方法中将每一步获得的奖赏反向传递给过去动作序列中的某些动作，不断进行迭代。此学习方法效率较低，在学习初期，需要较多的探索后才能获取第一个有效奖赏。扩展到大状态空间或者连续状态空间时，此问题会更加突出。针对该问题，一种被证明行之有效的方法是利用塑造奖赏机制，将模型知识以奖赏的形式反馈给学习器，减少次优动作的选择次数，从而加快学习系统的收敛速度。Randløv等人指出了如果塑造奖赏机制使用不当，将会对学习过程产生误导[15]。Ng等人研究了融入塑造奖赏机制的算法保持策略不变性的充要条件[16]。如何构造塑造奖赏以及如何及时准确地将模型知识传递给学习器，是这类方法的关键之处。径向基函数(RBF, radial basis function)网络利用一组 RBF将输入空间的非线性逼近问题转化为特征空间的线性逼近问题[17]。RBF网络不仅可以有效解决输入空间的非线性逼近问题，又保持了线性逼近模型的简单性及强泛化能力。在处理具有连续状态空间的强化学习问题时，RBF网络非常适合用来构造塑造奖赏机制中的势函数。

强化学习的在线特性决定了 RBF网络逼近模型会面临“灾难性扰动”问题，即新样本作用于学习模型后非常容易对之前学习到的输入输出映射关系产生破坏。本文提出利用自适应归一化径向基函数(ANRBF, adaptive normalized radial basis function)网络作为势函数来塑造奖赏。在RBF网络中融入归一化和自适应机制后，能够提供一个更加平滑且可微的势函数。ANRBF网络自适应地将模型知识传递给学习器，可以有效提高算法的初始性能及收敛速度。线性梯度下降方法简单、泛化能力强，适用于连续状态空间强化学习问题，而且在满足一定条件下收敛性可以得到保证。基于ANRBF网络提出了梯度下降版的强化学习算法——ANRBFGD-Sarsa(λ)。本文从理论上分析了 ANRBF-GDSarsa(λ)算法的收敛性。将 ANRBF-GD-Sarsa(λ)算法应用于 Mountain Car仿真平台，实验结果表明，ANRBF-GD-Sarsa(λ)算法具有较好的初始性能及收敛速度。

2 相关理论

2.1 Sarsa(λ)算法

传统的强化学习方法考虑的是具有离散状态空间和离散动作空间的强化学习问题[1]。当问题的状态空间扩展到连续空间时，原有的一些概念的定义形式将不再适用，本文需要对这些概念进行重新定义。具体定义如下。

定义 1 状态向量。状态是强化学习系统中的重要元素，是表征系统某一时刻特征及属性的最少数目变量的有序集合，以向量形式表示。假设系统状态由n个实数变量描述，则在t时刻系统的状态向量表示为在不关心时刻的情况下，统一用来表示状态向量。

定义 2 状态空间。强化学习问题P的状态空间为该问题所有可能状态的集合。假设系统状态表示为n维状态向量 x =[x1, x2,… ,xn]T，则P的状态空间即为以状态向量各分量为坐标轴而形成的n维向量空间的某个子空间，记作 X ( P) ⊆ Rn。形式化定义为 X ( P ) = { x| x = [ x1, x2,…,xn]T,xi∈ Di, i = 1,… ,n}其中， Di是状态向量第i个分量的值域。在不强调特定问题时，用X表示状态空间。∀Di，若至少一个为连续域，那么X称为连续状态空间；若全部为连续域，X称为完全连续状态空间；若无连续域，X称为离散状态空间。

仿照定义1和定义2，可以定义动作向量和动作空间。本文关注的是具有连续状态空间和离散动作空间的强化学习问题。若无特别说明，本文统一用来表示问题的动作空间。

用强化学习方法解决实际问题，主要分为预测问题和控制问题2部分。TD学习方法作为强化学习中的一类很重要的算法，在各种学习任务中都能很好地解决预测和控制问题。强化学习算法收敛的必要条件是所有状态或状态动作对被无限次访问，即需要平衡探索与利用。可以通过在策略(on-policy)和离策略(off-policy) 2类方法来平衡探索和利用[1]。Sarsa算法是经典的在策略TD控制学习算法，传统的Q学习和Sarsa算法只向前看一步或者 TD误差仅向后传递一步。为了获得一个更高效的学习算法，需要综合考虑整个行动轨迹，于是引入资格迹，产生了更一般的Sarsa(λ)算法[1]。同样以马尔科夫决策过程为基础，通过试错来不断地与环境进行交互，最终学习到一个最优策略。在实际问题中，Sarsa(λ)算法通过迭代来学习，迭代方法如式(1)

2.2 梯度下降方法

利用梯度下降方法来解决强化学习问题时，首先要对算法中的值函数进行线性建模[1]。模型如式(2)

其中，θt为在t时刻的n维权值向量，φ(x,u)为状态动作对＜x,u＞的n维特征向量。在式(2)所示模型的基础上通过最小化均方误差(MSE, meansquared error)来逼近最优值函数[1]。MSE形式化定义如式(3)

在式(5)的条件下，若学习率α随时间衰减，那么可以证明采用梯度下降方法的线性学习模型是收敛的[9]。

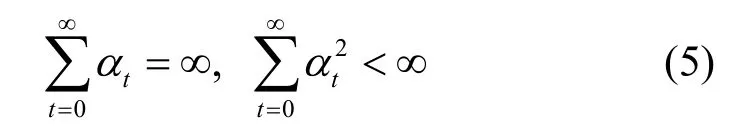
3 自适应势函数塑造奖赏机制

定义3 势函数(PF, potential function)。PF来源于物理学中的势，在保守场中，单位质点在A点与参考点的势能之差是一定的，把这个势能差定义为保守场中A点的“势”。强化学习中通过一个实值函数Φ：X↦R来表征Agent处于某一情境所具有的势，其中，X为任意状态空间。Φ(x)越大说明状态x越接近目标状态，这里的实值函数Φ称作势函数，具体问题需要具体定义。

定义4 基于势函数的塑造奖赏(PF-SR, potential function based shaping reward)。基于势函数Φ：X ↦R定义一个有界实值映射F： X×U×X↦R，其中，X为任意状态空间，U为离散动作空间，塑造奖赏定义为式(6)

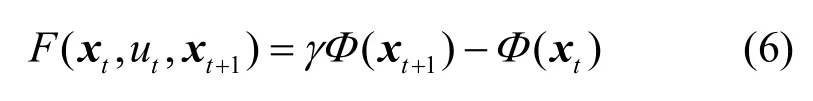
其中， γ ∈ ［ 0,1］为折扣率。塑造奖赏就是当前状态和后继状态势的折扣差值。

定义 5 基于塑造奖赏的连续状态马尔科夫决策过程(SR-CS-MDP, shaping reward based continuous state markov decision process)。SR-CS-MDP 为一个四元组 M ' = ｛X , U , R', T ｝，其中，X为任意连续状态空间，U为任意离散动作空间，R'：X×U×X↦R为在原始奖赏函数R的基础上融入塑造奖赏之后的奖赏函数， R '( x , u , x ' ) = R ( x , u,x')+F ( x , u,x')， T ： X × U ↦ P D( X)为状态转移函数。在SR-CS-MDP中的一个典型的交互过程为：在时间步t，Agent感知到当前的状态xt∈X，根据当前行为策略 π ( xt, ut) = p( ut|xt)，选择一个动作ut∈U，将ut作用于环境，环境对此做出响应，根据状态转移函数， xt以概率 T ( xt, ut, xt+1)转移至xt+1∈X ，并给出立即奖赏值 R '( xt, ut, xt+1)。

下面以n维连续状态空间为例，阐述一种利用ANRBF网络构建势函数的方法，引入ANRBF网络之前需要给出状态空间高斯划分的定义，ANRBF网络与状态空间高斯划分一一对应。

1) Bi≠Bj, i ≠ j, i, j = 1,2,… , m ，即所有划分分块两两不重合；

2)Ω ( φi( x )) ⊃ Bi, i = 1,2,… ,m ，即任意高斯函数的状态空间投影真包含对应的划分分块，其中，Ω为投影算子；

下面通过2个例子来说明状态空间高斯划分，如图1所示，图1(a)和图1(b)分别为利用3个一维和 9个二维等距高斯函数平均划分状态空间X = ｛ x| x = [ x ] ,x ∈[-2,2]｝和X = { x| x =[x, x]T,

1 11 2 x1, x2∈[-2 ,2]}的划分示意图。

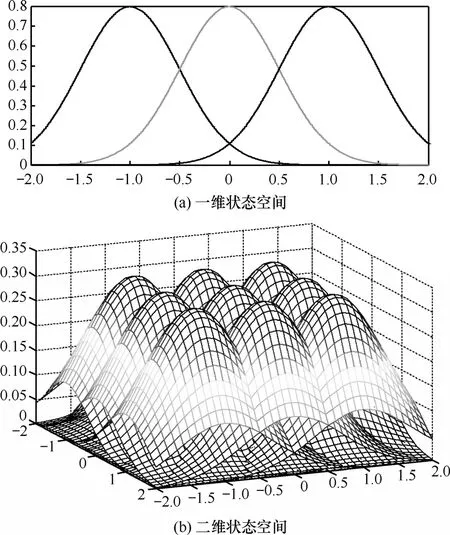
图1 状态空间高斯划分

基于上述状态空间高斯划分，可以导出对应的RBF网络。在此基础上，将状态空间高斯划分确定的基函数进行归一化处理，然后引入自适应机制，构建一个ANRBF网络。具体定义如下。

定义 7 ANRBF网络。ANRBF网络是一种n× 1m× 的三层归一化带反馈机制的神经网络，它可在线自适应地调整隐藏层各节点的权值。ANRBF网络的结构如图2所示。

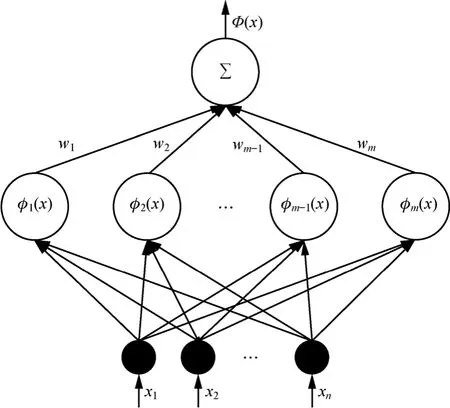
图2 ANRBF网络结构

1) 最底层称为输入层，表示n维输入向量，这里是状态向量

2) 中间层称为隐藏层，共m个隐节点。每个隐节点内置一个激活函数，这里采用高斯RBF。隐节点激活函数定义如式(7)

这里的激活函数就是对应高斯划分中的基函数经过归一化而得到的，其中，n维向量分别表示状态空间高斯划分中的第i个子空间的中心向量及其宽度。

3) 最上层称为输出层，对隐藏层各节点进行加权求和，表示为其中， wi是经状态空间高斯划分后生成的各个子空间分块的权重。隐藏层的每个激活函数和输出权值，与对应的状态空间划分紧密耦合，知识就是通过这样的一种耦合机制进行传递的。

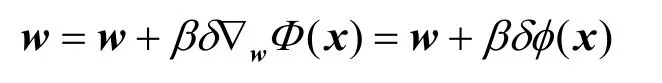
其中，δ为学习过程中产生的TD误差；β ∈ ［ 0,1 ］为步长参数，控制梯度调整的速度，β越大，调整越快，但越容易引起震荡；梯度向量为

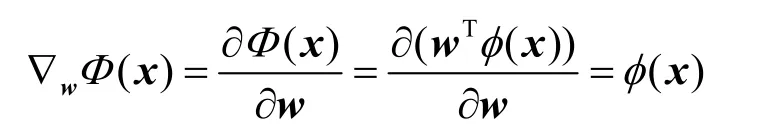
4 自适应势函数塑造奖赏机制下的梯度下降 Sarsa(λ)算法

4.1 算法框架

本文所提出的算法可构建为一个行动者-评论家(actor-critic)模型，算法框架如图 3所示。行动者(actor)感知到环境(environment)的当前状态(state)，根据不断修正优化的策略(policy)来选择一个动作(action)，并将此动作作用于环境，环境对此做出响应，给出一个立即奖赏(reward)，环境状态转移至一个后继状态。评论家模型包含2个评论子模型，一个是利用梯度下降的值函数(value function)模型，另一个是产生塑造奖赏的势函数(potential function)模型。值函数模型在收集到状态、动作、奖赏等信息后，计算出TD误差oldδ。势函数模型在收集到状态、动作、奖赏等信息后，计算出塑造奖赏SR。然后利用 SR重塑(remodel)TD误差，得到新的 TD误差δnew。δnew反作用于2个评论子模型以及策略模块，评论子模型及策略模块根据δnew进行修正优化。算法按上述流程不断循环，直至收敛到一个最优策略。

图3 算法框架

4.2 ANRBF-GD-Sarsa(λ)算法

考虑具有连续状态空间X和离散动作空间U的强化学习问题。值函数模型为Q(x,u)= θTφ(x,u)，其中，势函数模型为Φ(x)=wTφ(x)，其中，算法详细描述如下。

算法 1 ANRBF-GD-Sarsa(λ)：基于 ANRBF网络塑造奖赏机制的梯度下降Sarsa(λ)算法

1) 状态空间进行高斯划分，初始化ANRBF网络隐藏层各节点的激活函数φ(⋅)]T；

m

3) 构建带有 Hash机制的10个 8×8的 Tiling编码模块；

5) 重复（对每一个情节）；

6) 初始化当前状态x及动作u；

7) 重复（对该情节中的每一步）；

8) 执行动作u，观察r， x '；

9) 将数据 ＜ x ' ,U(x ' )＞输入当前值函数模型；

10) u '←通过动作选择策略选择状态 x '下的动作；

11) 收集数据 ＜ x , u , x ' ,r, u'＞ ；

12) 计算TD误差， δold=r + γQ( x ',u')-Q ( x , u)；

13) 计算SR， F (x , u,x ' ) = γΦ(x ' )-Φ(x)；

14) 计算新TD误差， δnew=δold+F （ x, u ,x '）；

15) 更 新资 格 迹 ， e ← γ λe + ∇wQ ( x , u)= γ λe+φ(x , u)；

16) 将δnew反馈给值函数模型及势函数模型；

17) 调整权值，θ←θ+αδnewe，w ← w + βδnewφ(x)；

18) x= x'， u = u '；

19) 直到x是终止状态；

20) 直到运行完设定情节数或满足其他终止条件。

4.3 Tile编码机制

上一节描述的 ANRBF-GD-Sarsa(λ)算法中的φ（x, u ）为状态动作对＜x,u＞的特征向量。本算法的值函数模型首先利用Tile编码机制来对状态x进行编码，得到状态x的特征向量。然后根据不同的动作，利用 Hash机制将得到的状态特征向量映射到h维的状态动作对的特征向量空间，从而得到＜x,u＞的特征向量φ（x , u ）。

Tile编码简单高效，能够高度契合在线学习任务的特性[18]。下面详细描述利用Tile编码机制提取状态特征向量的过程：假设状态空间为n维矩形区域，按照随机偏移规则，采用 i（≥ 1 ）个比状态空间略大的n维矩形区域重叠覆盖整个状态空间。这里的矩形区域称为Tiling，共有i个Tiling。每个Tiling被划分为 j（≥ 1 ）个Tile，每个Tile表示的是状态特征向量中的某一特征分量的接受区域。这里得到的状态特征向量为i× j维。如果状态x出现在第k （ 1≤ k ≤ i × j）个Tile的接受区域中，则将x的特征向量中的第k个分量置为1。编码完成后，i×j维的状态特征向量中仅有i个分量被置为1，其余都为0。

以任意2维连续状态空间为例，Tile编码模型如图4所示。图中横坐标表示状态的第1维，纵坐标表示状态的第2维，阴影部分为状态空间，阴影部分中的每一个点都是一个状态。使用10个8× 8的Tiling来编码，10个Tiling按照随机偏移规则来覆盖状态空间。为了方便起见，图中只画了2个Tiling。状态编码过程如下：在设置好的10个Tiling中，查找状态落在哪10个Tile的接受区域，在对应的640维二进制编码中将对应位置置1，其余位置置0。经过Tiling编码得到的状态特征向量具有一定的稀疏性，这样不仅可以有效控制特征向量的有效长度，而且有利于降低计算复杂度。Tile编码中使用的Tiling数目越多，编码的精度就越高，但计算复杂度也会越高。

图4 状态空间Tile编码

4.4 算法收敛性分析

下面从误差更新的角度切入，与经典的 GDSarsa(λ)算法[1]进行比较，分析 ANRBF-GD-Sarsa(λ)算法的收敛性，并证明ANRBF-GD-Sarsa(λ)算法与利用势函数进行初始化的 GD-Sarsa(λ)算法具有一致的收敛性。

定理 1 在确定性马尔科夫决策过程中，如果算法具有相同的学习经验序列，那么 ANRBF-GDSarsa(λ)算法与利用势函数进行初始化的 GDSarsa(λ)算法具有一致的收敛性。

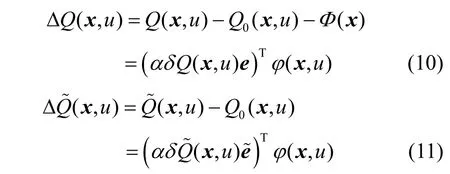
1) 当值函数Q(x,u)和Q˜(x,u)都是初始模型时，即

2) 假设到目前为止，∀ x ∈ X , u ∈ U，有ΔQ(x,在此基础上，当前时间步获得了一个新的经验五元组，此时TD误差计算如下

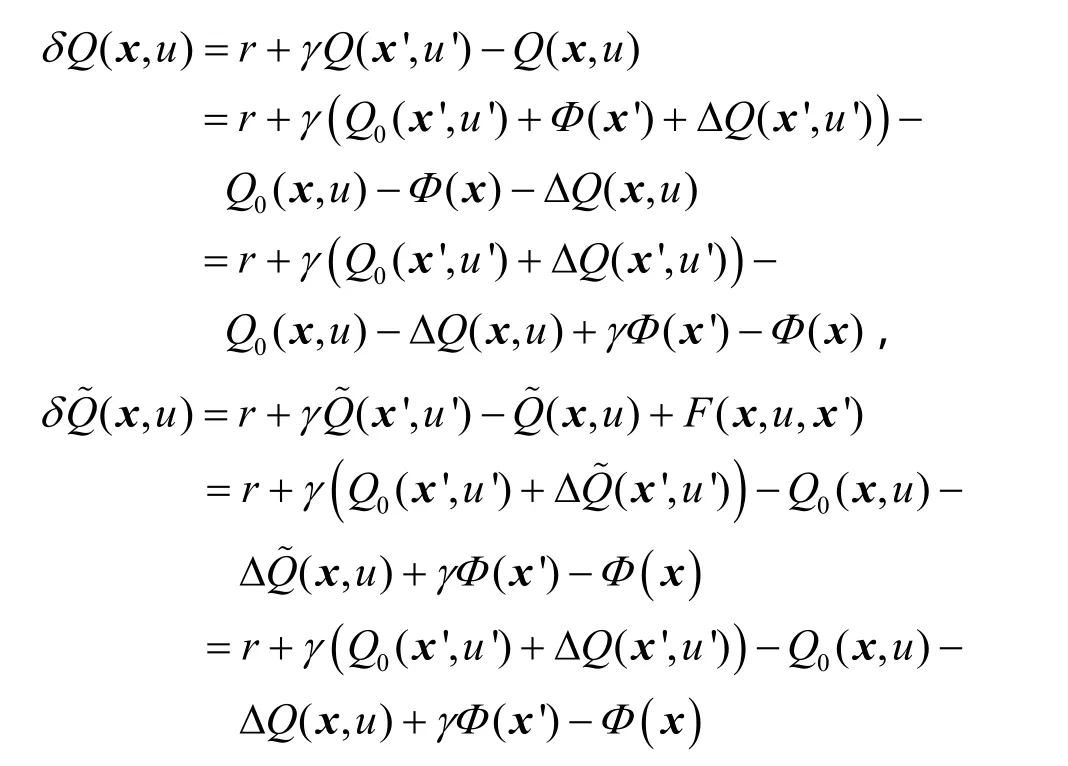
定理2 在式(5)所示的条件下，如果学习率α可以随时间衰减，那么本文所提的 ANRBF-GDSarsa(λ)算法至少能够收敛到原问题的一个局部最优解。

证明 从文献[9]得知，强化学习中采用梯度下降训练方法的线性学习算法，比如Sutton等提出的GD-Sarsa(λ)算法，在满足式(5)的条件下，如果学习率α可以随时间衰减，那么能够保证该算法至少能够收敛到原问题的一个局部最优解。又因为定理 2证明了在具有相同经验序列的情况下，ANRBFGD-Sarsa(λ)算法与利用势函数初始化的GD-Sarsa(λ)算法具有一致的收敛性。而强化学习算法中任意初始化的值函数都不会改变算法的收敛结果，因此，ANRBF-GD-Sarsa(λ)算法在满足式(5)的条件下，如果学习率α可以随时间衰减，至少能够收敛到原问题的一个局部最优解。

5 实验及结果分析

5.1 实验描述

为了验证所提算法的性能，针对具有二维连续状态空间与一维离散动作空间的Mountain Car问题进行仿真研究。Mountain Car问题除了系统的状态观测值以外，没有任何有关系统动力学模型的先验知识，因此难以采用传统的基于模型的最优化控制方法进行求解。图5给出了Mountain Car问题的示意。

图5 Mountain Car示意

图 5中的曲线代表一个山谷的地形，其中，S为山谷最低点，G为右端最高点，A为左端最高点。小车的任务是在动力不足的条件下，从S点以尽量短的时间运动到G点。系统的状态由2个连续变量y和v表示，其中，y为小车的水平位移，v为小车的水平速度，状态空间约定如式(12)

当小车位于S点、G点和A点时，y的取值分别为-0.5、0.5和-1.2。动作空间为｛u1, u2, u3｝，包含3个离散的控制量，即 u1=+1、u2= 0 和 u3=-1，表示小车所受水平方向的力，分别代表全油门向前、零油门和全油门向后3个控制行为。仿真实验中，系统的动力学特性描述如式(13)

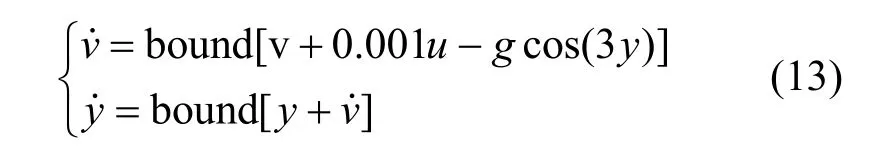
其中， g = 0 .0025为与重力有关的系数，u为控制量，v˙为新的水平速度，y˙为新的水平位移。目标是在没有任何模型先验知识的前提下，控制小车以最短时间从S点运动到G点。上述控制问题可以用一个确定性MDP来建模，奖赏函数如式(14)

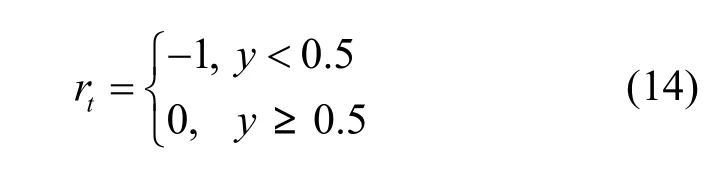
5.2 实验设置

将本文所提ANRBF-GD-Sarsa(λ)算法与 Sutton等人提出的 GD-Sarsa(λ)算法[1]及 Maei等人提出的Greedy-GQ 算法[14]在相同的实验环境下分别独立重复做30次仿真实验，并比较不同参数值对算法的影响。仿真实验中，每次实验设定的情节数为1 000，每个情节的最大时间步数设置为 1 000。小车的初始状态设为 0.5y=- 和 0v= ，当小车到达G点或时间步数超过1 000时，一个情节结束。然后系统状态重新进行初始化，开始下一个情节的学习。学习完设定的1 000个情节后，一次实验结束。学习算法的性能由3个指标来评价：①收敛速度，即算法能够在多少个情节内收敛；②收敛结果，即算法收敛后，小车从初始点到达目标点G所用的时间步；③初始性能，即每次实验的前5个情节中，小车从初始点到达目标点G所用的时间步。

本问题的状态空间为一个二维连续空间，首先将状态空间进行高斯划分，在每一维分别用8个等距的高斯基函数来对状态空间进行划分，则本问题势函数定义如式(15)

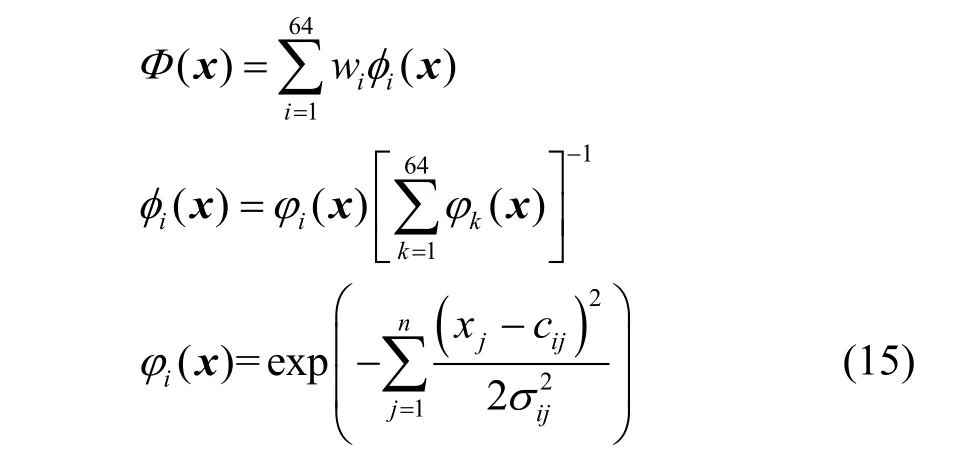
其中， ci=[ci1,… ,cin]T是宽度为 σi=[σi1, … ,σin]T的高斯函数φi的中心位置。

针对式(12)所示的二维连续状态空间，使用10个8 8×的Tiling来编码，10个Tiling按照随机偏移规则来覆盖状态空间。状态编码过程如下：在设置好的10个Tiling中，查找状态落在哪10个 Tile的接受区域，在对应的640维二进制编码中将对应位置置1，其余位置置0。本实验中每个状态经过10个8 8×的Tiling编码后，采用Hash机制进行变换，得到对应的特征向量。

实验中状态动作对的特征向量维数设置为 3 000维，即 φ (x,u)∈R3000，折扣率γ=1.0，衰减因子λ= 0 .9，权值向量为 θ ∈ R3000，初始化为0。采用如式（15）所述的8× 8个等距的高斯基函数来对二维状态空间进行高斯划分，得到ANRBF网络势函数模型。高斯基函数的宽度向量设为 σ =[0.1,0.1]T，ANRBF输出层权值向量w ∈ R8×8，初始化为0，ANRBF学习率为β=0.05。另外，考虑到本问题奖赏值设定如式(14)所示，结合问题特性，行为策略使用ε-greedy ，ε=0，即贪心策略。由于学习过程中得到的奖赏都是 -1，权值向量初值都为0，故初始值函数为0，而最终真实值函数都是负的，所以在学习初期即使ε=0也保证了有效的探索。随着值函数不断地逼近真实值，此行为策略将指导小车获得最优爬山路径。

5.3 实验分析

ANRBF-GD-Sarsa(λ)算法、GD-Sarsa(λ)算法及Greedy-GQ算法的30次仿真实验结果如图6所示。图6分3行3列共9幅图，横坐标表示情节数，最大设为1 000，纵坐标为每个情节小车从谷底爬到目标点G所走的时间步数，最大时间步设为1 000。图6 3列对应算法的学习率取值分别为0.05/10 0.005= 、0.15/10 0.015= 及0.5/10 0.05= ，这里的10是状态编码环节所用的Tiling数目；1行、2行、3行分别是 Greedy-GQ 算 法 、GD-Sarsa(λ)算 法 及ANRBF-GD-Sarsa(λ)算法，其中，每一幅图是某一种算法在对应学习率下的30次仿真实验的学习结果。从图6列向比较中可以看出，在相同学习率下，ANRBF-GD-Sarsa(λ)算法初始性能及收敛速度最好，GD-Sarsa(λ)算法次之，Greedy-GQ算法最差；从图6行向比较中可以看出，3个算法随着学习率的增大收敛速度明显加快，Greedy-GQ算法反差最为明显，GD-Sarsa(λ)算法反差稍小，ANRBFGD-Sarsa(λ)算法反差最小，可见，ANRBF-GDSarsa(λ)算法对学习率的适应性较强。

上述30次仿真运行结果的均值比较如图 7所示。图7从上向下共3幅图，学习率分别为0.005、0.015、0.05，从图中可以直观地看出，在收敛速度和初始性能方面，ANRBF-GD-Sarsa(λ)算法相比GD-Sarsa(λ)算法及Greedy-GQ算法效果更好，而在最终收敛效果方面，学习率为0.005时，本文所提算法 ANRBF-GD-Sarsa(λ)与 GD-Sarsa(λ)算法优于Greedy-GQ算法，而在学习率为0.015及0.05时，3种算法收敛结果基本相同。

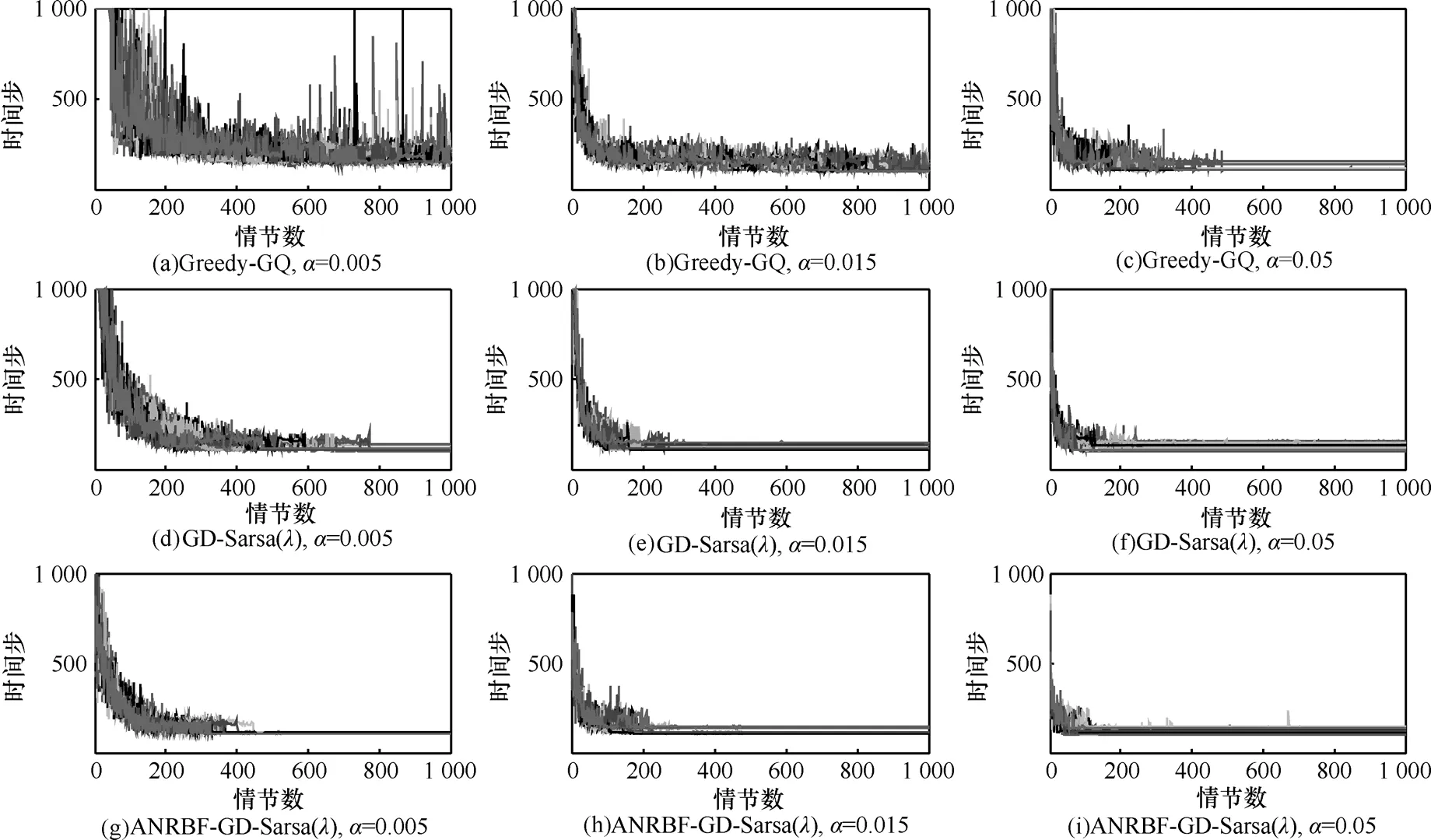
图6 Mountain Car问题中3种算法的性能比较

图7 Mountain Car问题中3种算法的性能比较

表1 3个算法收敛所需情节数比较

表2 3个算法收敛后到达目标点所需时间步比较

表3 3个算法前5个情节到达目标点所需时间步比较

图6和图7展示的实验结果详细数据分析见表1～表3。3张表列出了3个算法采用不同学习率独立运行30次仿真实验所得结果的统计值。表1列出了30次实验中算法收敛所需要的情节数的最大、最小及平均值；表2列出了30次实验中算法收敛后，小车从谷底爬到山顶G所需的时间步数的最大、最小及平均值；表3重点比较3个算法的初始性能，关注30次仿真实验中的前5个情节时间步数的平均值。因为结果曲线存在一定的随机和震荡性，所以这里最大、最小和平均值统一用一个区间表示。当学习率为0.005及0.015时，Greedy-GQ算法在设定的1 000个情节内并未收敛，在图6中反映为曲线图震荡比较厉害，在表中标识为N。从表 1和表 2中可以看出，学习率为 0.005时，ANRBF-GD-Sarsa(λ)算法可以在大约367个情节收敛，收敛后大约 113个时间步到达目标点。GD-Sarsa(λ)算法需要大约 762个情节收敛，收敛后大约113个时间步到达目标点。Greedy-GQ算法没有收敛；学习率为0.015时，ANRBF- GD-Sarsa(λ)算法可以在大约172个情节收敛，收敛后大约123个时间步到达目标点。GD-Sarsa(λ)算法需要大约200个情节收敛，收敛后大约120个时间步到达目标点。Greedy-GQ算法没有收敛；学习率为 0.05时，ANRBF-GD-Sarsa(λ)算法可以在大约110个情节收敛，收敛后大约 125个时间步到达目标点。GD-Sarsa(λ)算法需要大约 112个情节收敛，收敛后大约129个时间步到达目标点。Greedy-GQ算法需要大约357个情节收敛，收敛后大约115个时间步到达目标点。从表 3中可以看出，30次仿真实验平均结果中，比较算法前5个情节的时间步，ANRBF-GD-Sarsa(λ)最优。综上所述，3个算法收敛后到达目标点时间步数基本相同，而在初始性能及收敛速度方面，ANRBF-GDSarsa(λ)明显优于 GD-Sarsa(λ)算法及 Greedy-GQ算法。

6 结束语

本文旨在通过势函数塑造奖赏机制来提高强化学习算法的初始性能及收敛速度。创新之处在于利用 ANRBF网络将输入空间映射到高维特征空间，通过一组高斯基函数的线性组合构建势函数。在一定程度上利用了环境模型的先验知识，从而可以有效提高算法初始性能及收敛速度。基于ANRBF网络和线性梯度下降方法提出了 ANRBFGD-Sarsa(λ)算法。从理论上分析了 ANRBF-GDSarsa(λ)算法的收敛性，并通过连续状态空间、离散动作空间的Mountain Car仿真问题对算法的有效性进行了验证。与 GD-Sarsa(λ)算法及 Greedy-GQ 算法进行了比较，结果表明，本文所提算法具有更优的性能。

函数逼近为解决连续状态空间强化学习问题提供了一个有效的途径。近来利用各种有监督学习方法来逼近状态（动作）值函数成为强化学习领域的研究热点，函数逼近可以大大提高算法的学习速度，但是也面临算法复杂化及理论上难以保证收敛等问题，如何在保证算法的收敛性下有效提高算法的收敛速度，是未来强化学习函数逼近研究的热点。如何设计更好的势函数，以及势函数如何自学习，从而更好地将模型知识传递给学习器，以提高算法初始性能及收敛速度也是研究的热点。

[1] SUTTON R S, BARTO A G. Reinforcement Learning： An Introduction[M]. Cambridge： MIT Press, 1998.163-223.

[2] 刘全, 傅启明, 龚声蓉等. 最小状态变元平均奖赏的强化学习方法[J].通信学报, 2011, 32(1)： 66-71.LIU Q, FU Q M, GONG S R, et al. Reinforcement learning algorithm based on minimum state method and average reward[J]. Journal on Communications[J], 2011, 32(1)： 66-71.

[3] SILVER D, SUTTON R S, MÜLLER M. Temporal-difference search in computer go[J]. Machine Learning, 2012, 87(2)： 183-219.

[4] 陈宗海, 文锋, 聂建斌等. 基于节点生长 k-均值聚类算法的强化学习方法[J]. 计算机研究与发展, 2006, 34(4)： 661-666.CHEN Z H, WEN F, NIE J B, et al. A reinforcement learning method based on node-growing k-means clustering algorithm[J]. Journal of Computer Research and Development, 2006, 34(4)： 661-666.

[5] 刘全, 闫其粹, 伏玉琛等. 一种基于启发式奖赏函数的分层强化学习方法[J]. 计算机研究与发展, 2011, 48(12)： 2352-2358.LIU Q, YAN Q C, FU Y C, et al. A hierarchical reinforcement learning method based on heuristic reward function[J]. Journal of Computer Research and Development, 2011, 48(12)： 2352-2358.

[6] KRETCHMAR R M. Parallel reinforcement learning[A]. World Conference on Systemics, Cybernetics, and Informatics[C]. New York,2002. 114-118.

[7] GEIST M, PIETQUIN O. Parametric value function approximation： a unified view[A]. IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning[C]. Paris, 2011. 9-16.

[8] 王雪松, 田西兰, 程玉虎等. 基于协同最小二乘支持向量机的Q学习[J]. 自动化学报, 2009, 35(2)： 214-219.WANG X S, TIAN X L, CHENG Y H, et al. Q-learning system based on cooperative least squares support vector machine[J]. Acta Automatica Sinica, 2009, 35(2)： 214-219.

[9] TSITSIKLIS J N, VAN ROY B. An analysis of temporal-difference learning with function approximation[J]. IEEE Transactions on Automatic Control, 1997, 42： 674-690.

[10] SUTTON R S, Mcallester D, SINGH S, et al. Policy gradient methods for reinforcement learning with function approximation[A]. Annual Conference on Neural Information Processing Systems[C]. Denver,1999. 1057-1063.

[11] BONARINI A, LAZARIC A, MONTRONE F, et al. Reinforcement distribution in fuzzy Q-learning[J]. Fuzzy Sets and Systems, 2009,160(10)： 1420-1443.

[12] HEINEN M R, ENGEL P M. An incremental probabilistic neural network for regression and reinforcement learning tasks[A]. International Conference on Artificial Neural Networks[C]. Thessaloniki,2010. 170-179.

[13] MAEI H R, SUTTON R S. GQ(λ)： a general gradient algorithm for temporal difference prediction learning with eligibility traces[A]. International Conference on Artificial General Intelligence[C]. Lugano,2010. 91-96.

[14] MAEI H R, SZEPESVARI C, BHATNAGAR S, et al. Toward off-policy learning control with function approximation[A]. International Conference on Machine Learning[C]. Haifa, 2010. 719-726.

[15] RANDLØV J, ALSTRØM P. Learning to drive a bicycle using reinforcement learning and shaping[A]. International Conference on Machine Learning[C]. San Francisco, 1998. 463-471.

[16] NG A Y, HARADA D, RUSSELL S. Policy invariance under reward transformations： theory and application to reward shaping[A]. International Conference on Machine Learning[C]. San Francisco, 1999. 278-287.

[17] HUANG G, SARATCHANDRAN P, SUNDARARAJAN N. A gener-alized growing and pruning RBF (GGAP-RBF) neural network for function approximation[J]. IEEE Transactions on Neural Networks,2005, 16(1)： 57-67.

[18] SHERSTOV A A, STONE P. Function approximation via tile coding：automating parameter choice[A]. International Symposium on Abstraction, Reformulation and Approximation[C]. Berlin, 2005.194-205.