基于帝国竞争算法的车架优化

孙 丽，王 珂，孟广伟，李 锋，郝 岩，刘忠振

（1.徐工集团工程机械股份有限公司 建设机械分公司，江苏，徐州 221002；2.吉林大学 机械科学与工程学院，吉林，长春 130022）

车架作为汽车的主要部分，承载着汽车发动机及其它各个部件。为了寻求既安全又经济的结构形式，汽车车架轻量化设计具有重要意义。

近年来，涌现出很多对车架轻量化的方法。刘齐茂[1]采用有限元软件ANSYS的零阶方法对车架部件的截面尺寸进行优化。向湘林、左孔天[2]提出自适应响应面法对货车车架进行优化。由于传统的优化方法容易陷入局部最优解，因此，进化算法也有了很大的发展。在遗传算法不断改进的基础上，田阔[3]运用改进的遗传算法对车架结构进行了优化。所使用的优化方法逐渐由传统的规划方法向进化方法发展，努力替代以往靠经验优化和设计车架的手段。帝国竞争算法是由Atashpaz-Gargari 和Lucas[4]于2007年提出的一种政治社会进化算法，该算法借鉴于现实世界中帝国主义国家扩张和掠夺殖民地的历史进程，通过大量殖民地向帝国的靠近，来寻找到全局最优解，帝国之间的竞争促成了算法的收敛。不少学者也对此算法进行了改进[5-6]。本文通过帝国竞争算法对车架各个部件厚度进行优化设计，构造新的轻型货车车架结构，使车架部件受力更加合理，提高了材料利用率，节约了成本。在保证车架的各项基本性能[7-9]的情况下，实现了轻型货车车架结构的轻量化设计。

1 帝国竞争算法

帝国竞争算法是最近几年提出的高级启发式最优化算法。此算法的思想源于人类政治社会进化的过程，即历史上帝国对殖民地的掠夺和帝国之间的竞争。

1.1 建立初始帝国

最优化的目的是要寻求目标函数最优解。在此，首先建立一个N维设计变量的数组表示国家。

计算每个国家的成本函数

每个国家的权力与其成本函数成反比例关系。成本低的前几个国家成为帝国主义国家，其余国家成为殖民地。按照帝国主义国家权力的大小划分殖民地。我们定义每个帝国主义国家的规范化成本为

式中，Mimp为总的帝国数。分配给每个帝国的殖民地数量为

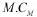
1.2 同化

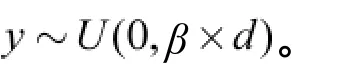
式中，{V}为有殖民地指向帝国的方向向量。

1.3 换帝

当殖民地向帝国靠近时，若有一个殖民地的成本低于帝国成本，在此情况下，该殖民地与帝国交换位置，原来的帝国成为殖民地，而成本小的殖民地成为新的帝国。

1.4 竞争

一个帝国的权力与该帝国的总成本大小成反比，帝国的总成本为

在竞争中，每个帝国都有可能占据最弱帝国中的最弱殖民地。为了衡量每个帝国的权力，首先将总成本规范化为

根据每个帝国的权力，形成权力向量P

创建一个与P相同大小的概率矩阵R

D中最大值相对应的帝国将获得拥有权。该帝国会获得最弱帝国中的最弱的殖民地。

1.5 合并

在不断的竞争中，最弱的帝国会逐渐失去所有的殖民地。最后，该帝国会被其它帝国吞并而成为殖民地。

1.6 收敛

经过N年后，即迭代N次后，当仅剩一个帝国统领所有殖民地时，算法结束。

2 车架有限元分析

本文所研究的某轻型载货汽车的车架为边梁式，由2根纵梁和6根横梁组成。汽车额定载重量为1 t，车架总长度为4.633 m，宽度为1.69 m，高度0.17 m。车架所选用的材料为Q235-A，许用屈服应力为235 MPa。车架有限元模型如图1所示。

车架承受着来自发动机、驾驶室、驾乘人员、油箱、货箱（满载）等载荷，根据静力等效原则[10]，将以上各个载荷施加在有限元模型相应接触面的节点上。相应的载荷数据见表1，载荷施加位置如图2所示。

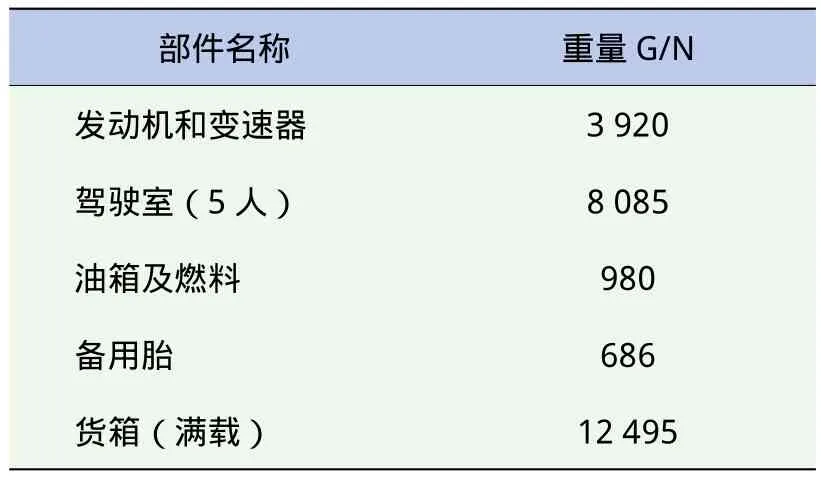
表1 车架所受载荷

2.1 弯曲工况

弯曲工况[11]是研究汽车满载时承受静载荷时车架的抗弯特性。这是检验车架刚度最主要的工况之一。利用有限元分析软件对本文有限元模型进行分析计算，选取4个车轮的轮心为4个支撑点。车架弯曲工况边界条件是约束4个车轮垂直方向的位移，约束右侧两个车轮的横向位移，约束左前轮和右前轮的纵向位移。经分析计算弯曲工况应力分布云图、位移分布云图如图3和图4所示。最大应力出现在车架第2个横梁与纵梁接触处，为27.161 MPa；最大位移出现在车架的尾部，为0.77 mm。

2.2 扭转工况

扭转工况[12]是研究车满载时承受扭转载荷时车架的抗扭转变形的特性，主要考察车架左右纵梁在固定载荷下的扭转状况，所受载荷与弯曲工况相同。利用有限元分析软件对本文有限元模型进行分析计算，选取4个车轮的轮心为4个支撑点。车架扭转工况边界条件是约束左侧两个车轮和右前轮垂直方向的位移，约束左前轮和右前轮纵向位移，约束左侧两个车轮横向位移，完全释放右后轮的全部自由度。经分析计算扭转工况应力分布云图、位移分布云图如图5和图6所示。最大应力出现在第4个横梁与纵梁接触处，为121.091 MPa；最大位移出现在第5个横梁与纵梁接触处，为12.228 mm。

3 基于帝国竞争算法的车架优化

3.1 优化参数设置

根据某轻型货车车架确定将要优化的纵梁和横梁的数量和位置，然后对纵梁和横梁的各个板厚尺寸进行优化。各个部件的板厚列于表2中。设计变量[13-14]取值范围均是2～6 mm，状态变量是最大位移12.228 mm 和最大应力121.091 MPa，目标函数是轻型货车车架的质量。帝国竞争算法的初始国家数量为200，其中帝国数量为3，殖民地数量为197，迭代次数为50。

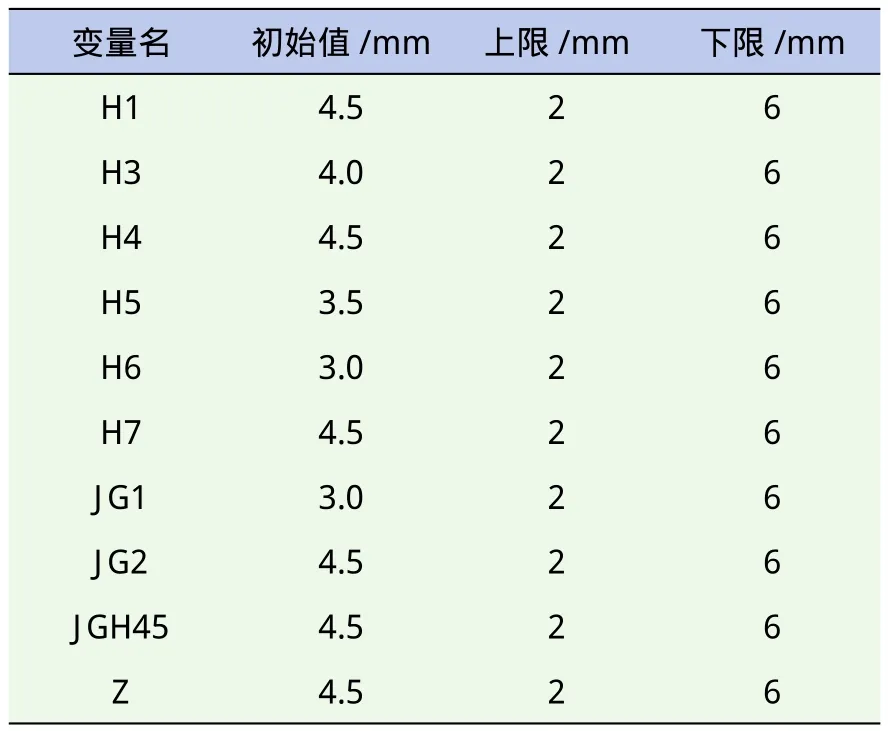
表2 车架各个板的厚度

3.2 车架优化步骤

首先，根据表2生成若干组初始板厚，各自创建独立的国家。计算各个国家的成本，即不同设计方案下的车架质量。然后选取质量最小的前Mimp个国家作为帝国，建立初始帝国。帝国建立之后，每个帝国中的殖民地向其帝国靠近，若发现某一殖民地的质量低于该帝国质量，交换二者位置。接着帝国之间进行竞争，消除权力小的帝国，直到剩下一个帝国而终止。此时该帝国即为最优解。

车架优化问题是一约束优化问题，在初期生成若干组设计方案时，有些方案会不满足结构设计的要求。因此，本文采用罚函数法处理约束条件，成本函数为

基于帝国竞争算法的车架优化基本流程如图7所示。

3.3 结果与分析

本文将帝国竞争算法的结果与有限元分析软件ANSYS优化算法中的零阶算法[15]进行了比较，在设计变量的取值范围和状态变量相同的情况下，两种算法得到的结果列于表3。

表3 两种算法的结果比较

从表3中可以看出，通过优化计算，有限元分析软件ANSYS优化算法中的零阶算法将总质量减少了5.4%，帝国竞争算法计算总质量减少了8.3%，结果好于前者。说明帝国竞争算法具有较好的全局寻优能力。

4 结论

本文在考虑某轻型货车静态时实际工况的基础上，建立以最小化车架质量为目标函数的优化模型。然后利用帝国竞争算法对车架主要部件的厚度进行优化计算，以达到车架轻量化的目的。通过与ANSYS零阶方法的对比，验证了帝国竞争算法的适用性，体现了该算法更好的全局收敛能力。通过算例表明，帝国竞争算法能够以较高的精度收敛到全局最优点，体现了很好的实用价值和适用性。

References)

[1]刘齐茂. 汽车车架的结构优化设计[J]. 机械设计与制造，2005，43(4)：1-3.Liu Qimao. Structure Optimization Design for the Automotive Frame[J]. Machinery Design & Manufacture，2005，43(4)：1-3. (in Chinese)

[2]向湘林，左孔天. 基于自适应响应面法的货车车架优化研究[C]. 第八届中国CAE工程分析技术年会论文集，2012：90-94.Xiang Xianglin，Zuo Kongtian. Truck Frame Optimization Based on the Adaptive Responsive Surface Method[C].Proceedings of he 8th CAE Engineering Analysis Technology Annual Conference，2012：90-94. (in Chinese)

[3]田阔. 基于遗传算法的车架结构优化[D].天津：河北工业大学，2010.Tian Kuo. Frame Structure Optimization Based on Genetic Algorithm[D]. Tianjin：Heibei University of Technology，2010. (in Chinese)

[4]ATASHPAZ-GARGARI E，LUCAS C. Imperialist Competitive Algorithm：an Algorithm for Optimization Inspired by Imperialistic Competition[C]. IEEE Congress on Evolutionary Computation，Singapore，2007：4661-4667.

[5]ATASHPAZ-GARGARI E，HASHEMZADEH F.RAJABIOUN R，et al. Colonial Competitive Algorithm：a Novel Approach for PID Controller Design in MIMO Distillation Column Process[J]. Int J Intell Comput Cybernet，2008(3)1：337-55.

[6]KAVEH A，TALATAHARI S.Imperialist Competitive Algorithm for Engineering Design Problems[J]. Asian J Civil Eng，2010，11(6)：675-97.

[7]曲昌荣，郝玉莲，戚洪涛. 汽车车架的有限元分析[J].轻型汽车技术，2008，36(9)：9-12.Qu Changrong，Hao Yulian，Qi Hongtao. Finite Element Analysis of the Vehicle Frame[J]. Light Vehicle Technology，2008，36(9)：9-12. (in Chinese)

[8]桂良进，周长路，范子杰. 某型载货车车架结构轻量化设计[J]. 汽车工程，2003，25(4)：403-406.Gui Liangjin，Zhou Changlu，Fan Zijie. Lightweight Design for Frame Structure of a Heavy-Duty Truck[J]. Automotive Engineering，2003，25(4)：403-406. (in Chinese)

[9]历辉，李万琼. 货车车架的等效载荷简化[J]. 汽车工程，1994，16(5)：310-314.Li Hui，Li Wanqiong. The Equivalent Load Determination of Truck Frame[J]. Automotive Engineering，1994，16(5)：310-314. (in Chinese)

[10]俆石安. 汽车构造-底盘工程[M]. 北京：清华大学出版社，2008.Xu Shian. Automobile Construction Chassis Engineering[M].Beijing：Tsinghua University Press，2008.(in Chinese)

[11]叶勤. 轻型载货汽车车架有限元分析与优化[D]. 武汉：武汉理工大学，2007.Ye Qin. Finite Element Analysis and Optimization of Light Truck's Frame[D]. Wuhan：Wuhan University of Technology，2007. (in Chinese)

[12]张旭. 某轿车车身有限元分析[J]. 农业装备与车辆工程，2009，47(7)：26-28.Zhang Xu. Finite Element Analysis of a Car Body[J]. Agricultural Equipment & Vehicle Engineering，2009，47(7)：26-28. (in Chinese)

[13]张朝晖. ANSYS12.0 结构分析工程应用实例解析[M].北京：机械工业出版社，2010.Zhang Chaohui. Engineering Applications of ANSYS12.0 Structural Analysis[M]. Beijing：China Machine Press，2010. (in Chinese)

[14]曾攀，雷丽萍，方刚. 基于ANSYS平台有限元分析手册：结构的建模与分析[M]. 北京：机械工业出版社，2011.Zeng Pan，Lei Liping，Fang Gang. Finite Element Analysis Guide：Modeling and Analysis of Structure[M]. Beijing：China Machine Press，2011. (in Chinese)

[15]王虎奇. 基于ANSYS零阶方法的装载机前车架的结构优化设计[J]. 今日科苑，2007，11(8)：114.Wang Huqi. Structural Optimizaion Design of the Front Frame of a Wheel Loader Based on the ANSYS Zero Order Method[J]. Today Panorama of Modern Sciences，2007，11(8)：114. (in Chinese)