有限群的弱s-置换嵌入子群

钟 国，杨立英，韦华全，2，马儇龙，周 洋

(1. 广西师范学院数学科学学院，广西 南宁 530023；2. 广西大学数学与信息科学学院，广西 南宁530004)

有限群的弱s-置换嵌入子群

钟 国1，杨立英1，韦华全1，2，马儇龙1，周 洋1

(1. 广西师范学院数学科学学院，广西 南宁 530023；2. 广西大学数学与信息科学学院，广西 南宁530004)

群G的一个子群H称为在G中s-置换嵌入,如果对于任意的素数p||H|,H的Sylowp-子群也是G的某个s-置换子群的Sylowpp-子群.称群G的子群H在G中弱s-置换嵌入,如果存在群G的次正规子群T和包含在H中的G的一个s-置换嵌入子群Hse,使得G=HT且H∩T≤Hse.利用弱s-置换嵌入子群的概念,研究了超可解群的构造,获得了有限群为p-超可解的一些充分条件.

p-超可解群;弱s-置换嵌入;有限群

0 引 言

群G的子群H与K称为可置换的,如果HK=KH.若H与G的每个子群可置换,则称H是G的置换子群.1939年,Ore[1]证明了有限群的每个置换子群都是次正规的.1962年,Ito[2]证明了对有限群G的每个置换子群H,H/HG是幂零群.后来,Kegel[3]又给出了s-置换子群的定义:群G的子群H称为在G中s-置换,若H与G的每个Sylow子群可置换.进一步地,Ballester-Boinches等[4]从嵌入子群的角度引入了s-置换嵌入子群的概念:称群G的子群H在G中s-置换嵌入的,如果对于|H|的每个素因子p,H的Sylowp-子群也是G的某个s-置换子群的Sylowp-子群.2009年,李样明等[5]引入了弱s-置换嵌入子群的概念,分别统一推广了正规子群、置换子群、s-置换子群、s-置换嵌入子群、c-正规子群和c*-正规子群,从而统一推广了若干熟知的重要结果.通过对弱s-置换嵌入子群的考察,利用子群弱s-置换嵌入性,推广了最近一些结论．文中G总表示一个有限群,符号和术语都是规范的.

1 预备知识

定义1[5]设H是G的子群.称H在G中弱s-置换嵌入,如果存在群G的次正规子群T和包含在H中的G的一个s-置换嵌入子群Hse,使得G=HT且H∩T≤Hse.

明显,正规子群、置换子群、s-置换子群、s-置换嵌入子群、c-正规子群和c*-正规子群都是弱s-置换嵌入子群.但是,反之不然[5].

引理1[6-7]

1)s-置换子群是次正规子群;

2) 设P是G的p-子群,其中p∈π(G).则P在G中s-置换当且仅当NG(P)≥Op(G);

3) 设H在G中s-置换,P∈Sylp(H),p为素数.如果P≤Op(G)或HG=1,则P在G中s-置换;

4) 设HsG是包含在H中的G的最大s-置换子群,则HsG是唯一包含在H中的G的最大s-置换子群,特别地,NG(H)≤NG(HsG).

5) 设H为G的s-置换嵌入子群,则HN在G中s-置换嵌入,HN/N在G/N中s-置换嵌入.

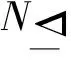
1) H≤M≤G,H在M中弱s-置换嵌入;

2) H≤G且N≤H,则H/N在G/N中弱s-置换嵌入;

3) 设π是一素数集合,若H是G的π-子群,而N为π′-子群,则HN/N在G/N中弱s-置换嵌入.

引理3[8]设N(N≠1)是G的可解正规子群,如果N∩Φ(G)=1,则N的Fitting子群F(N)是包含在N中G的极小正规子群的直积.

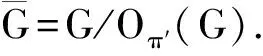
引理5[10]设G是一个有限群,P是一个素数,满足对于不小于1的整数n,有(|G|,(p-1)(p2-1)…(pn-1))=1.假设G有一个Sylowp-子群P,使得P的每个n-极大子群在G中弱s-置换嵌入,则G是p-幂零的.

引理7[6]设N是群G的正规子群,H是G的p-子群,K是G的子群使得G=HK.如果H∩N是N的Sylowpp-群,那么HN∩KN=(H∩K)N.

2 主要结果

定理1 设H是群G的p-可解正规子群使得G/H为p-超可解.若F(H)的包含Op′(H)的极大子群都在G中弱s-置换嵌入,则G是p-超可解.

证明假设结论不真.设G为极小阶反例.

1) Op′(G)=1.

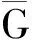
2) H∩Φ(G)=1.

G=KNG(S)=TNG(S)=NG(S),

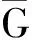
3) 最后的矛盾.

Gp≤NG(P1)≤NG((P1)sG),

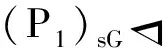
F(H)=R1×…×Rt,

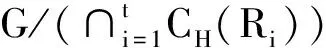
推论1 设H是群G的p-可解正规子群使得G/H为p-超可解.若Fp(H)的Sylowp-子群的极大子群皆在G中弱s-置换嵌入,则G为p-超可解.

证明因为Fp(H)为p-幂零,所以Fp(H)的包含Op′(H)的极大子群形如P1Op′(H),其中P1为Fp(H)的某个Sylowp-子群的极大子群.由假设,P1在G中弱s-置换嵌入,于是存在群G的次正规子群T和包含在P1中的G的一个s-置换嵌入子群(P1)se,使得G=P1T且P1∩T≤(P1)se.于是有G=(P1Op′(H))K.显然,Op′(H)≤T,故P1Op′(H)∩T=(P1∩T)Op′(H).因为(P1∩T)Op′(H)≤(P1)seOp′(H),由引理1，(P1)seOp′(H)在G中s-置换嵌入,这样P1Op′(H)在G中弱s-置换嵌入.由定理1即得G为p-超可解群.完成证明.

推论2(见文献[7]定理3.6) 设G是p-可解群.若F(G)的包含Op′(G)的极大子群都在G中弱s-置换,则G是p-超可解.

推论3(见文献[6]定理4.2.8) 设H是群G的p-可解正规子群使得G/H为p-超可解.若F(H)的包含Op′(H)的极大子群都在G中c*-正规,则G是p-超可解.

推论4(见文献[6]推论4.2.9) 设H是群G的p-可解正规子群使得G/H为p-超可解.若Fp(H)的Sylowp-子群的极大子群皆在G中c*-正规,则G为p-超可解.

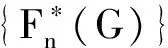
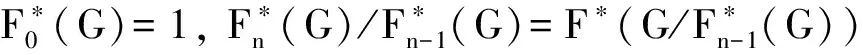
则

定理2 设是包含的饱和群系,H是群G的正规子群使得G/H∈.若对某个(H)的Sylow子群的极大子群都在G中弱s-置换嵌入,则G∈.

证明设G是极小阶反例.首先,由引理2及引理5有:

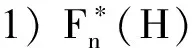
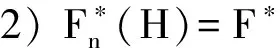
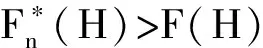
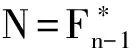
(ii) G/Q∈,其中且Q∈Sylq(F(H)).

3) 完成证明.

推论5(见文献[6]定理5.3.3) 设是包含的饱和群系,H是群G的正规子群使得G/H∈.若对某个的Sylow子群的极大子群都在G中c*-正规,则G∈.

定理3 设是包含的饱和群系.群G∈当且仅当F*(G)的每个极小子群及4阶循环子群在G中弱s-置换嵌入.

证明充分性显然.

设H为F*(G)的极小子群或4阶循环子群.由假设,存在群G的次正规子群T和包含在H中的G的一个s-置换嵌入子群Hse,使得G=HT且H∩T≤Hse.由引理6,G/TG为素数幂阶群,于是G/TG∈F.若TG=1,则G∈.若TG≠1,从而G≤T,G=HT=T,于是有H=H∩T≤Hse.这表明F*(G)的每个极小子群及4阶循环子群在G中s-置换嵌入.可以利用文献[12]定理1.2得G∈.

推论6(见文献[6]定理5.4.4) 设是包含的饱和群系.群G∈当且仅当F*(G)的每个极小子群及4阶循环子群在G中c*-正规.

[1] Ore O. Contributions in the theory of groups of finite groups[J]. J Duke Math,1939，5(2):431-460.

[2] Dekins W E. On qusinormal subgroups of finite groups[J]. Math Z,1963，82(2):125-132.

[3] Kegel O H. Sylow-gruppen und subnormalteiler endlicher gruppen[J]. Math Z,1962：78(1):205-221.

[4] Ballester-Bolinches A, Pedraza-Aquilera M C. Sufficient conditions for supersolvable of finite groups[J].J Pure and Applied Algebra,1998，127(2):123-118.

[5] Li Yangming, Qiao Shouhong, Wang Yanming. On weaklys-permutably embedded subgroups of finite groups[J]. Communications in Algebra,2009,37:1086-1097.

[6]韦华全.子群特性与有限群结构[D].广州：中山大学,2006.

[7] Miao Long. On weaklys-permutable subgroups of finite groups[J]. Bulletin of the Brazilian Mathematical Society,2010,41(2):223-235.

[8] Guo Wenbin. The theory of classes of groups[M]. Beijing-Boston: Science Press-Kuwer Acad Pub,2000.

[9] Gorenstein D. Finite groups[M]. New York: Chelsea,1980.

[10] 於遒,李长稳.有弱s-置换嵌入的准素子群的p-幂零群[J].安徽大学学报:自然科学版,2011,35(1):28-31.

[11] Skiba A N. On weaklys-permutable subgroup of finite groups[J]. J Algebra,2007,315:192-209.

[12] Li Yangming, Wang Yanming. On π-quasinormally embedded subgroups of finite group [J].J Algebra,2004,281(1),109-123.

Weaklys-PermutablyEmbeddedSubgroupsofFiniteGroups

ZHONG Guo1, YANG Liying1, WEI Huaquan1,2, MA Xuanlong1, ZHOU Yang1

(1. School of Mathematical Science, Guangxi Teachers Education University, Nanning 530023, China;2. Department of Mathematics and Information Science, Guangxi University, Nanning 530004, China)

A subgroupHof a finite groupGis calleds-permutably embedded inGif for each primep||H|, a Sylowp-subgroup ofHis also a Sylowp-subgroup of somes-permutably subgroup ofG. A subgroupHof a groupGis said to be weaklys-permutably embedded inGif there is a subnormal subgroupTofGand ans-permutably embedded subgroupHseofGis contained inH,such thatG=HTandH∩T≤Hse. Using this concept, the paper investigated the structure ofp-supersolvable groups and obtained some sufficient conditions ofp-supersolvability on finite groups.

p-supersolvable groups; weaklys-permutably embedded subgroups; finite groups

2012-09-08

国家自然科学基金项目(10961007,11161006)；广西自然科学基金项目(0991101,0991102)；广西教育厅科研基金项目(201012MS140)；广西高校人才资助计划(5070).

杨立英(1974—)，女,副教授,主要从事有限群理论研究.E-mail:yangliying0308@163.com

10.3969/j.issn.1674-232X.2013.01.013

O152MSC2010: 20D10;20D20

A

1674-232X(2013)01-0065-05