关于一般化的绝对Cesáro求和

韦宝荣

(杭州师范大学理学院，浙江 杭州 310036)

关于一般化的绝对Cesáro求和

韦宝荣

(杭州师范大学理学院，浙江 杭州 310036)

利用Bor和Yu Dansheng引入的一些新的数列偶条件与拟f指数递增条件，推广了Bor的有关级数绝对Cesáro求和的结论.

数列偶条件;绝对Cesáro求和;求和因子；拟f指数递增

0 引 言

一个数列{λn}称为是有界变差的，记为{λn}∈BV,如果

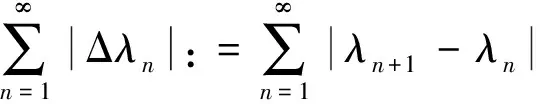
如果{λn}为一个有界变差趋于零的数列，则称{λn}∈BV0.

称正数数列{an}是几乎单调递增的，如果存在一个正的递增数列{cn}和两个正常数A与B使得Acn≤bn≤Bcn(见文献[1]).一个正数数列{γn}被称为是拟β指数递增的，如果存在一个常数K=K(γ)≥1使得对所有n≥m≥1成立Knβγn≥mβγm.众所周知，任何几乎递增的数列关于任何非负数β都是拟β指数递增的，但反之不真[2].

写着

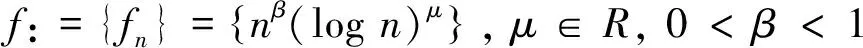
(1)

最近，Sulaiman[3]利用式(1)中定义的f进一步推广了拟β指数递增的概念.即，一个正数数列{γn}称为是拟f指数递增的，如果存在一个常数K=K(γ,f)≥1使得对所有n≥m≥1成立Kfnγn≥fmγm.该文中，如无特殊说明，数列f总由式(1)定义.

(2)

其中

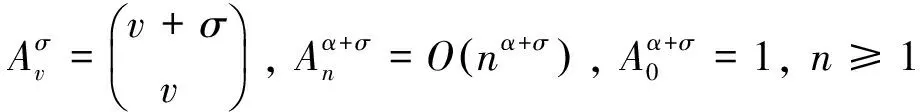
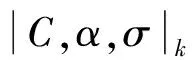
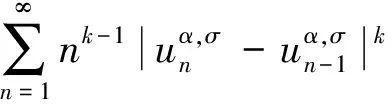
(3)

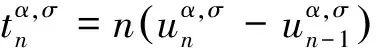
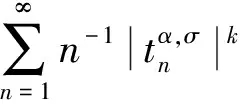
如果σ=0,则|C,α,σ|k求和即为通常的|C,α|k求和[6].

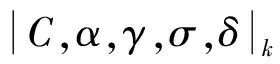
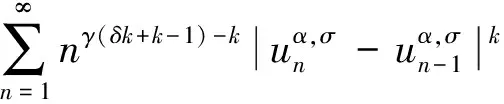
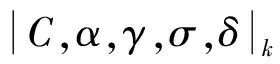
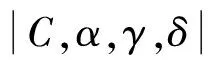
定理1 设{Xn}为一个几乎递增的数列，数列{δn}和{λn}满足下列条件：

(4)

δn→0,n→∞,

(5)

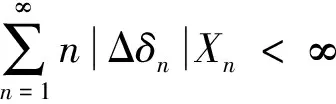
(6)

(7)

如果

(8)

那么级数∑λnan是|C,α,γ;δ|k可和的，其中k≥1,0≤δ<α≤1,γ为满足k+αk-γ(δk+k-1)>1的实数.

最近，Bor和Yu[8]引入了下面的有关数列偶的条件:

定义1 称一对数列λ:={λn}和X:={Xn}属于类M(θ,k),记为(λ,X)∈M(θ,k),如果λ和X满足下列条件

(9)

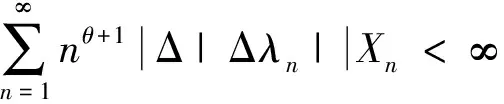
(10)

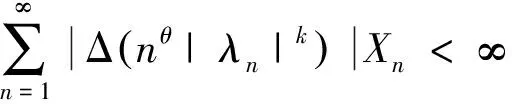
(11)

nθ|λn|kXn<∞.

(12)

如果λ和X只满足条件(9),(10)和(12)，那么称(λ,X)∈M*(θ,k).

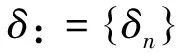
(13)

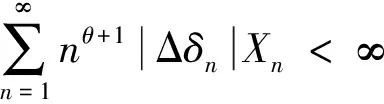
(14)

如果λ和X只满足条件λ∈BV，式(12)(13)和(14)，则称(λ,X)∈N*(θ,k,δ).

下面的有关M(θ,k),M*(θ,k),N(θ,k,δ)和N*(θ,k,δ)的性质都是有用的(见文献[8]的Proposition 1).

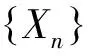
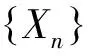
该文利用Bor和Yu[8]所定义的数列偶条件，进一步推广定理1，主要结论为：

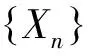
(15)

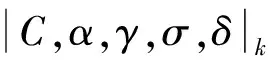
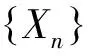
2 结论的证明

此处需要两个引理.

引理1[9]如果0<α≤1,σ>-1，1≤v≤n,那么

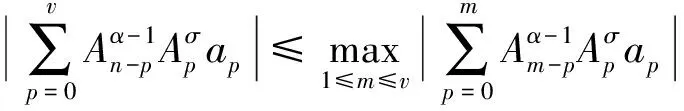
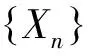
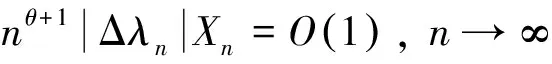
(16)

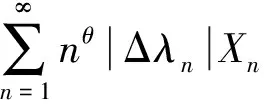
(17)

如果λ∈BV0，θ>β,那么

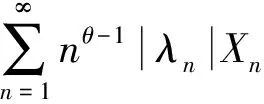
(18)

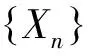
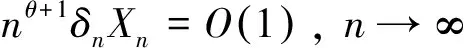
(19)

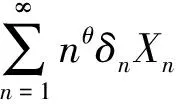
(20)

如果λ∈BV0，θ>β,那么

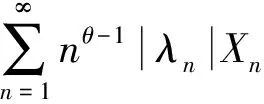
(21)

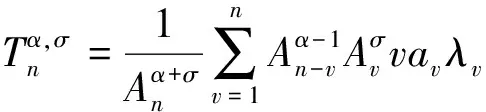
利用Abel变换和引理1，有

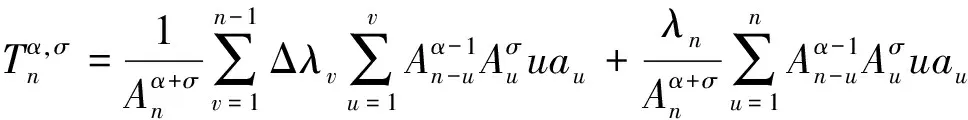
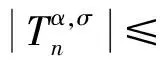
由于

只需证明

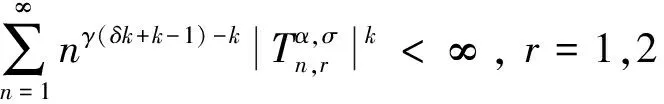
当k>1时，利用Hölder不等式(k=1时显然)，并且注意到λ∈BV,有

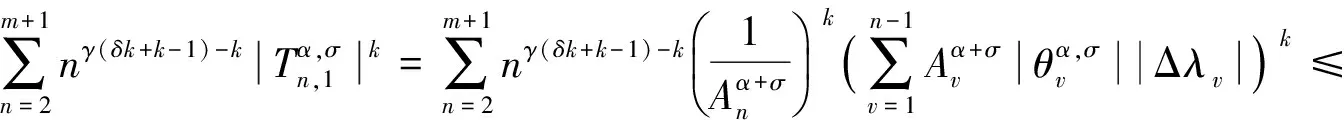
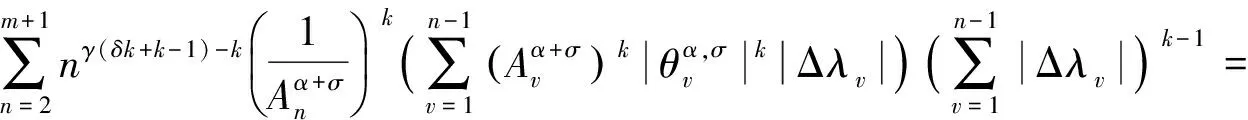
利用式(15)可推得

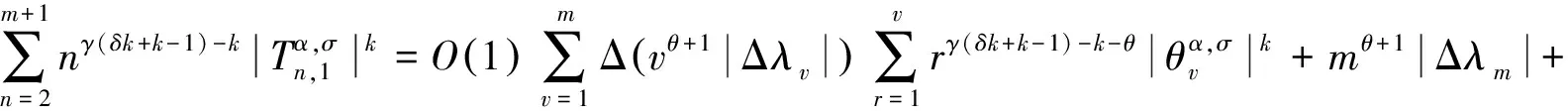
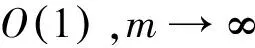
其中最后不等式中利用了式(10)(16)和(17).

利用式(11)(12)和(15),有

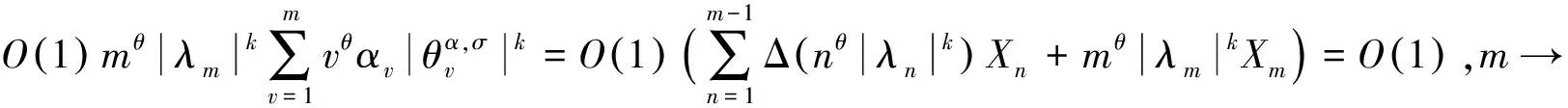
因此，

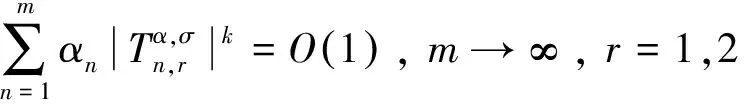
定理3证得.

由定理2的(c),即得定理3的第2个结论.

定理4的证明利用引理3，并且用δn代替|Δλn|，我们可以用类似于定理3的证明方法证明定理4，详细过程略去.

[1] Aljancic S, Arandelovic D.O-regularly varying functions[J]. Publ Inst Math,1977,22(1):5-22.

[2] Leindler L. A new application of quasi power increasing sequences[J]. Publ Math Debrecen,2001,58(4):791-796.

[3] Sulaiman W T. Extension on absolute summability factors of infinite series[J]. J Math Anal Appl,2006,322(2):1224-1230.

[4] Borwein D. Theorems on some methods of summability[J]. Quart J Math Oxfold,1958,9(2):310-316.

[5] Das G. A Tauberian theorem for absolute summability[J]. Proc Camb Phil Soc,1970,67(2):321-326.

[6] Flett T M. On an extension of absolute summability and some theorems of Littlewood and Paley[J]. Proc London Math Soc,1957,7(1):113-411.

[7] Bor H. Factors for generalized absolute Cesáro summability[J]. Math Communacation,2008,13(1):21-25.

[8] Bor H, Yu Dansheng.An application of generalized power increasing sequences on factors theorem[J]. Bull Belg Math Soc Simon Stevin,2013,20:1-8.

[9] Bor H. On a new application of quasi power increasing sequences[J]. Proc Estonian Acad Sci Phys Math,2008,57(3):205-209.

FactorTheoremsofaGeneralizedAbsoluteCesároSummability

WEI Baorong

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

By applying some new conditions on pairs of sequences introduced by Bor and Yu as well as quasif-power increasing sequence, the paper generalized a result of Bor on the factor for a generalized absolute Cesáro summability.

conditions on pairs of sequences; absolute Cesáro summability; summation factor; quasif-power increasing sequence

2010-09-02

韦宝荣(1960—),男,副教授,主要从事函数论研究.E-mail: weibr123456@126.com

10.3969/j.issn.1674-232X.2013.01.009

O174MSC2010: 40D15；40F05；40G05

A

1674-232X(2013)01-0045-05