基于Markov机制转换模型的黄金价格周期波动研究

严志辉

(申银万国证券股份有限公司 客户资产管理总部，上海 210031)

经济研究

基于Markov机制转换模型的黄金价格周期波动研究

严志辉

(申银万国证券股份有限公司 客户资产管理总部，上海 210031)

自20世纪70年代以来，黄金价格波动日益频繁。基于Markov机制转换模型对1975-2011年间黄金价格波动的特征进行分析,发现黄金价格波动在不同的机制(上涨、震荡状态、下跌)间周期转换。各种机制的平均持续时间不同,其中黄金价格上涨或者下跌的平均持续期是19周左右，黄金价格维持震荡状态的平均持续期约为24周，持续时间较长。另外，黄金价格波动所处的波动机制由诸多因素引起，但最重要的因素是由当时的世界经济状况，尤其是美国经济状况所决定的。

黄金；价格波动；Markov机制转换模型；机制波动特征

人类历史舞台中，黄金一直被视为财富的象征。黄金因兼具货币、金融商品和一般商品属性致使影响黄金价格波动的因素众多。众所周知，金本位制下黄金价格相对稳定。但自1973年“布雷顿森林体系”解体*布雷顿森林体系是以黄金为基础，以美元作为最主要的国际储备货币。在布雷顿森林体系下，美元直接与黄金挂钩，各国货币则与美元挂钩。美元可以兑换黄金和各国实行可调节的盯住汇率制，是构成这一货币体系的两大支柱。1971年8月金融市场上盛传法国等西欧国家要以大量美元兑换美国政府所储备黄金的消息，美国政府于8月15日不得不宣布停止履行对外国政府或中央银行以美元向美国兑换黄金的义务，自此黄金与美元“脱钩”。 1973年3月，西欧出现抛售美元，抢购黄金和马克的风潮。3月16日，欧洲共同市场9国在巴黎举行会议并达成协议，联邦德国、法国等国家对美元实行“联合浮动”，彼此之间实行固定汇率。英国、意大利、爱尔兰实行单独浮动，暂不参加共同浮动。其他主要西方货币实行了对美元的浮动汇率。至此，美元直接与黄金挂钩、各国货币与美元挂钩实行国际固定汇率的布雷顿森林体系彻底瓦解。后，黄金价格逐步市场化。自此以后，黄金价格及其影响因素的作用机制发生了深刻的变化。黄金价格波动加剧，并呈现出周期波动的特征。

Hamilton首先运用Markov机制转换模型研究了美国经济波动的机制及其周期，该研究为动态非线性、非对称、结构性突变时间序列变量波动等问题提供了一种全新的研究思路。[1]随后该模型广泛地应用于相关问题的研究，比较经典的研究如Kim、Nelson&Startz研究了1926-1986年间美国股市收益率波动的结构性特征。[2]Bredin&Fountas分析了过去40年中欧洲四国通货膨胀与影响通货膨胀因素之间的机制转换关系。[3]谢赤和刘潭秋研究了人民币实际汇率波动过程中的几种机制状态的转换特征。[4]赵留彦等考察了中国1985年以来的通胀率演化过程。[5]魏巍贤、陈智文、王建军研究了世界原油现货价格在1987-2006年间不同阶段的波动特征。[6]刘金全、刘志刚和于冬研究了1978-2004年间我国实际经济增长率存在着“非对称性”经济周期波动的特性。[7]上述研究表明， 运用Markov机制转换模型对结构性突变和参数时变性等相关问题的研究取得了比较科学的研究成果。基于此，本文基于黄金价格的影响因素及相互作用机制发生了深刻变化的事实，运用Markov机制转换模型揭示黄金价格周期波动的特征，为研究黄金价格周期波动与潜在的影响因素间的关系提供一个观测视角。

一 研究数据来源与Markov机制转换模型设定

(一)研究数据及其来源

本文选取1975年1月至2011年12月美国纽约商业交易所COMEX黄金期货每日收盘价来计算黄金日收益率。为了消除黄金价格短期波动的影响，本文将上述黄金日收益率转化为周收益率数据。这样处理既可以消除黄金价格短期波动，又可将非平稳的黄金价格转化为平稳、非自相关周收益率时间序列*考虑到论文的篇幅限制，相关数据的处理、数据时间序列的平稳性检验、自相关性检验的相关内容没有放入论文的正文。。

(二)Markov机制转换模型的设定

根据1975-2011年黄金价格波动的历史状况，本文将黄金价格波动分为上涨、震荡状态和下跌三种机制状态。由于黄金周收益率时间序列的非自相关性，结合Hamilton(1989)的研究，本文运用不存在滞后项的三状态Markov机制转换模型，模型如式(1)。在式(1)中yt为黄金周收益率。μst为黄金周收益率的均值，均值依赖于时间t期的机制状态St；σSt为测度黄金的周收益率波动(风险)大小的标准差，σt是独立同分布标准正态分布的随机变量序列。σSt也依赖于时间t期的机制状态St。其中St有三种机制状态：St=1表示黄金价格上涨；St=2表示黄金价格震荡状态；St=3表示黄金价格下跌。转换机制变量St对应着一个Markov过程，转换机制变量St的三种状态转移概率P为矩阵(2)。

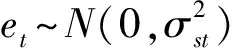
(1)

(2)

其中pij=p(St=(j|St-1=i)，pij表示由t-1期St-1=i状态转化至第t期状态St=j的概率。

(三)黄金价格各机制状态持续的平均时间E(T)

不失一般性，假定n种状态的机制变量St满足一阶Markov链过程，且当前经济处于第j种状态或机制。假定T为在第j种状态或机制持续的时间，那么持续时间T的概率为：

当T=1时，即St=j，St+1≠j，则概率p(T=1)=1-pjj

当T=2时，即St=St+1=j，St+2≠j，则概率p(T=2)=pjj(1-pjj)

……

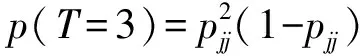
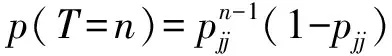
那么经济在状态j或机制j中平均持续时间E(T)可由下列公式(3)给出:

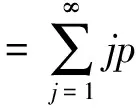
=1×(1-pjj)+2×pjj(1-pjj)+…

(3)

黄金价格波动第j种状态平均持续时间可由等式(3)计算得到。

二 黄金价格周期波动实证结果及讨论

(一)参数估计结果

基于Markov模型估计的思路，编制并运用Matlab程序对模型(1)的相关参数进行估计。参数估计结果如下表1所示。表中除了转移概率P13和P31外，所估计的参数均显著。

根据前面的假定:μ1=0.48%表示黄金价格处于上涨阶段时，黄金周收益率为0.48%。σ1=5.03%表明黄金价格处在上涨机制过程中会面临较大的不确定性。第二，μ2=0.17% 表明黄金价格处于震荡状态时，黄金周收益率为0.17%，这表明样本期间黄金价格处于震荡状态机制时，从统计学意义上讲黄金价格总体上呈现震荡小幅盘升的态势。σ2=2.18% 表明黄金震荡状态机制过程中波动幅度有所降低；第三,μ3=-0.11%表示黄金价格处于下跌机制过程中，周收益率为-0.11%。标准差σ3=1.06%表示黄金价格下跌过程中波动幅度要小很多。黄金价格变化的各种机制的转换概率都小于1，基于各机制间转换的概率能够得到以下几个推论:

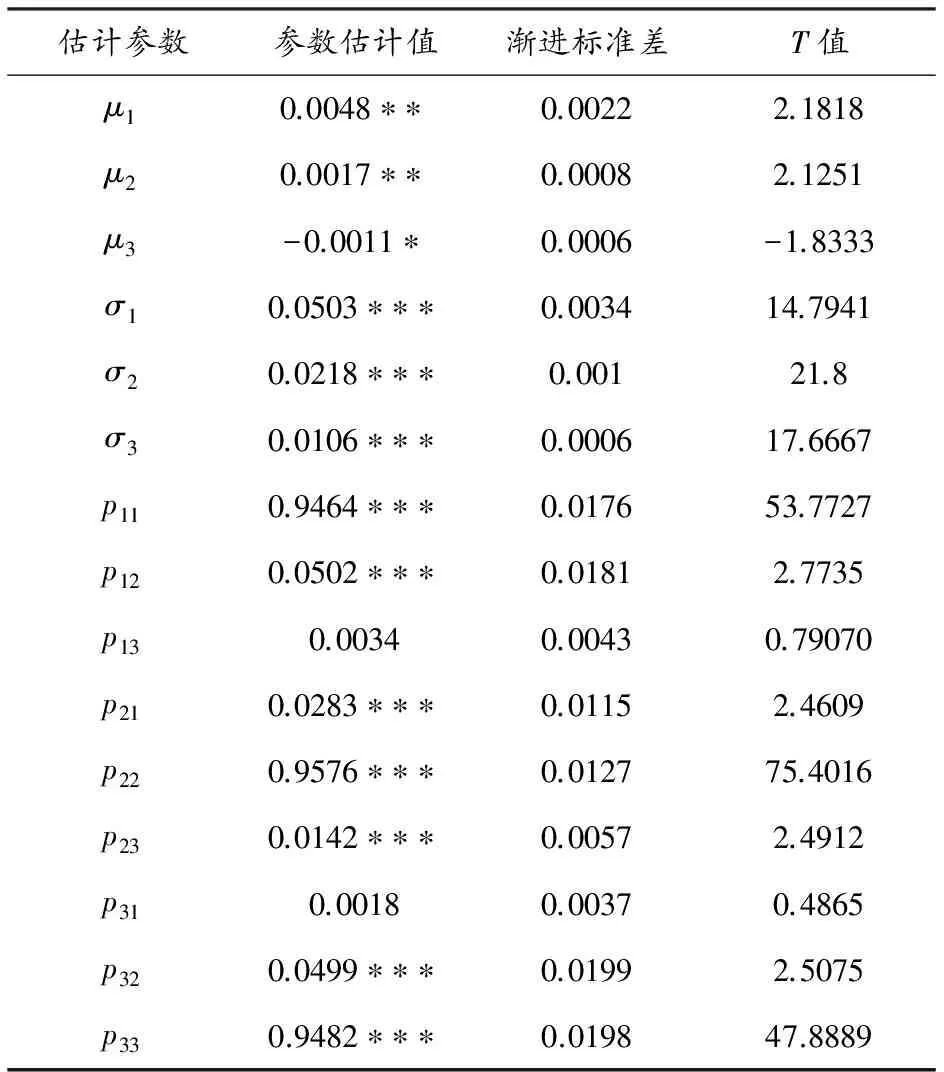
表1 参数估计结果

注：样本数大于120的t检验1%临界值是2.326，显著记为“***”; 5%临界值是1.96，显著记为“**”;10%临界值是1.645，显著记为“*”。表中的均值、方差为黄金处在不同波动机制下的周收益率的均值和方差。

(1)P11=0.9464表明本周黄金上涨(St-1=1)后下周继续上涨(St=1)的概率约为95%;

P12=0.0502说明本周黄金上涨后下周震荡的概率为5.02%；P13=0.0034表示本周黄金上涨后下周下跌的概率约为0 。由此可见，在黄金上涨之后未来主要还是持续价格上涨，且上涨的可能性要比震荡整理的可能性还大。本周黄金价格上涨后突然反转下跌的可能性几乎没有。

(2)P21= 0 .0283表示黄金价格本周(St-1=2)震荡后下周上涨(St=1)的可能性为2.83%;P22=0.9576表示黄金价格本周震荡整理后下周继续震荡整理的概率接近96%;P23=0.0142≈0表示黄金价格本周震荡整理后下周下跌的微乎其微。因此, 黄金价格处于震荡状态后,最可能的是维持震荡状态。

(3)P31=0.0018表示黄金本周下跌后(St-1=3)下周反转为升(St=1)的概率约为0.18% ;P32=0.0499表示黄金本周下跌后下周出现震荡整理的可能性为4.99% ;P33=0.9482表明黄金本周下跌后继续下跌的概率为94.8%。因此, 黄金价格本周下跌后,最可能的是继续下跌。转为震荡状态可能性很小，但反转为上涨的局面几乎不可能出现。

根据上面三个结论不难发现有一个共同的特征,当黄金价格波动处在某个特定的机制状态中的时候，向其他状态转移的可能性极小。

(二)黄金价格波动周期及三种状态转移概率图

根据等式(3)可计算得到黄金价格波动三种机制持续周期。上涨机制E(T1)持续的平均时间分别为18.7周；震荡状态机制E(T2)持续的平均时间分别为23.6周；下跌机制E(T3)持续的平均时间分别为19.3周。由此可见,黄金价格上涨、震荡、下跌三种机制的平均持续时间都比较长，这反映出黄金价格波动的趋势(机制)一旦形成，具有较强的持续性。这与自20世纪70年代至今的黄金价格波动特征基本相符。20世纪70年代至今的黄金价格波动表现出鲜明的机制周期性和轮换。黄金价格机制的周期性表现为黄金价格在某个阶段持续上涨或持续下跌，也可能持续震荡状态。黄金价格机制的轮换(机制转换)往往由外部各种影响黄金价格波动的因素或事件推动实现。如在20世纪70年代中后期“中东石油危机”、80年代初美国经济“滞涨”，这些因素及各种事件“驱动”黄金进入到持续上涨的机制状态，导致这个时期黄金长达3年多涨幅惊人、涨势迅猛的黄金价格牛市。随后随着上述事件影响效应的减弱，黄金价格陷入历时1年多的快速大幅回调，自20世纪90年代，全球经济进入快速平稳的发展阶段，国际政治形势相对平静，国际金融市场上投资者风险偏好较高，黄金作为避险资产的需求下降，黄金价格也因此进入长达十几年的震荡状态和下跌的机制状态中，直到2001年美国“9.11事件”爆发以及全球经济增长放缓等因素的出现，新外生影响“事件”和因素的出现再次推动了黄金从原来的以下跌和震荡为主要特征的机制状态，转换成当前以上涨机制和震荡为主要特征的机制状态。

根据机制转移概率的算法，可得图1、图2和图3黄金价格波动三个机制平滑概率图。图1是黄金价格上涨的平滑概率；图2是黄金价格下跌的平滑概率；图3是黄金价格震荡状态的平滑概率。通过观察平滑概率图，可更加清晰地了解每个机制的持续性以及每个时刻最可能出现的是哪种机制。基本判断法则是：如果St= 1 的平滑概率大于0.5，则表明黄金价格会出现上涨；如果St= 2 的平滑概率大于0.5，则表示出现黄金价格的震荡状态；如果St= 3的平滑概率大于0.5，则表示出现黄金价格呈现出明显的下跌趋势。

如图1和图2所示，本文可得以下基本结论： (1) 黄金上涨机制平滑概率形成的波峰最窄且波峰较为稀疏，震荡状态机制平滑概率形成的波峰最宽且波峰较为稠密，而黄金下跌机制平滑概率形成的波峰宽度和波峰稠密度介于黄金上涨机制和震荡状态机制之间。这表明黄金上涨机制和黄金下跌机制持续的时间较短,而黄金震荡状态机制持续的时间较长，这与前面根据转换概率计算出来结果是一致的。(2) 从总体上来说，三种机制交替出现，但第一、第三种机制出现的次数较少，即黄金价格持续上涨或下跌出现的次数较少。第二种震荡状态机制出现得最多，即黄金价格震荡状态是一种常态。另外，平滑概率图还很好地刻画出了特殊事件的影响。如图1中，在20世纪70年代中后期至20世纪80 年代初黄金价格大幅上涨概率值超过0.5的次数非常多, 这表明黄金价格在这个期间处在上涨机制的概率较高。这与当时国际政治经济事件如“两次中东石油危机”、1979年伊朗扣押美国人质事件以及后来美国经济的滞涨导致黄金价格在此期间快速上涨的历史表现基本吻合。

资料来源：作者根据Matlab程序运算的结果绘制

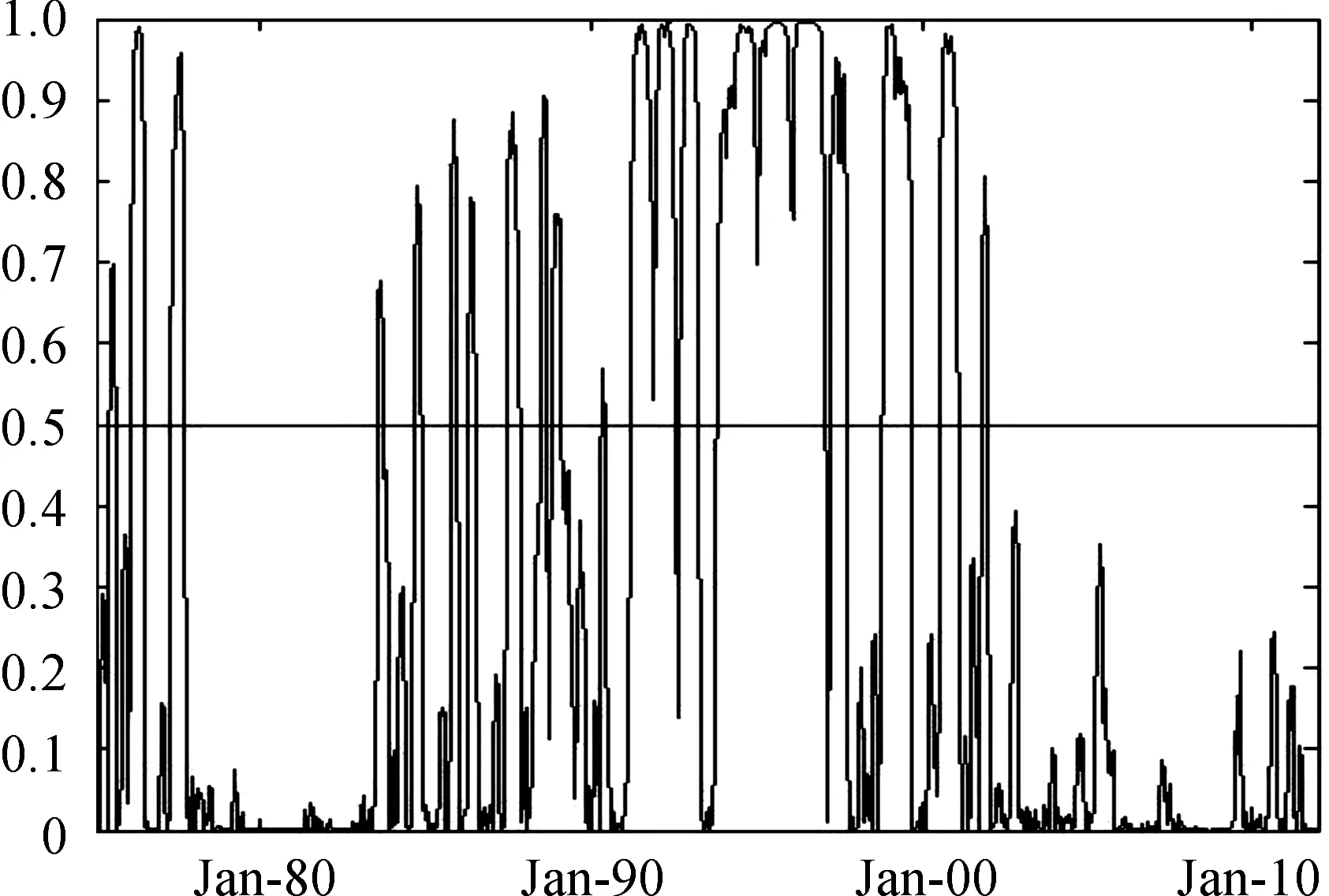
图2 黄金价格下跌机制(S3)平滑概率

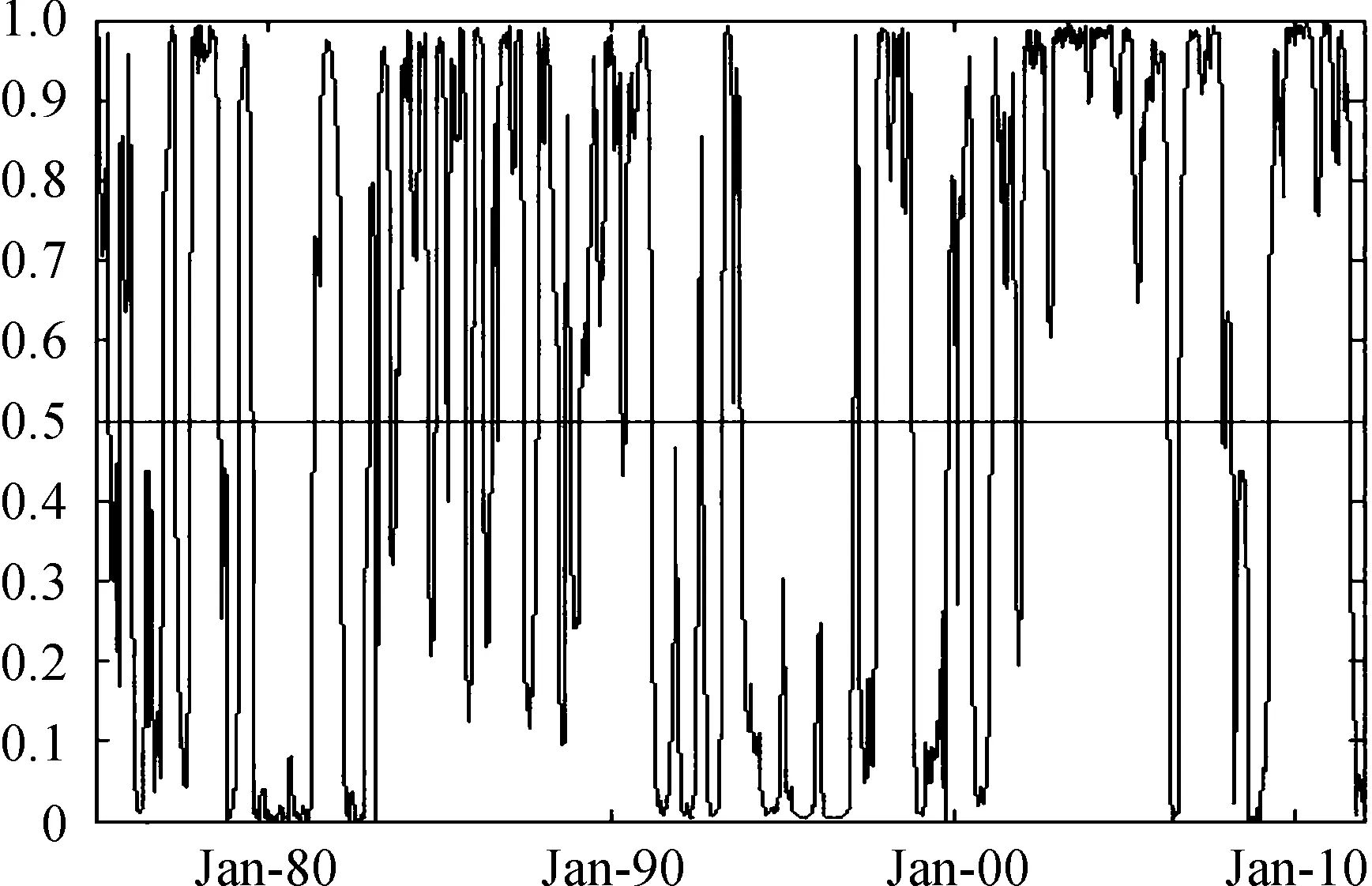
图3 黄金价格震荡状态机制(S2)平滑概率

三 基于Markov机制转换模型的黄金价格波动周期划分、影响因素及理论机制

根据Markov机制转换模型计算的三种机制转换的平滑概率图1、图2及图3，按照机制转换判断的规则，对1975-2011年间黄金价格波动机制状态进行划分，并对同期影响黄金的主要影响因素及影响的理论机制进行了分析，如表2所示。

表2表明，黄金价格的周期波动所处的机制由诸多因素引起，但最重要的因素是当时世界的经济状况，尤其是美国的经济状况。从表2来看，黄金价格波动所处的机制主要与美国经济周期所处的阶段相关。一般来说以美国经济为代表的世界经济处在比较好的发展时期的时候，黄金价格波动大体在震荡下跌的机制中。相反，2008年后美国经济、世界经济发展遇到问题，增长趋势的前景黯淡时，黄金价格往往处在震荡上升的机制中。其次，表2的研究结论表明，相对一般的自回归模型，Markov模型相对变量时间序列的刻画更细致，可以将黄金价格波动历史区分为上涨、震荡状态和下跌，并与同期国际政治格局、经济周期及其走势相对照，为研究黄金价格周期波动与潜在的影响因素间的关系提供一个新的观测视角。

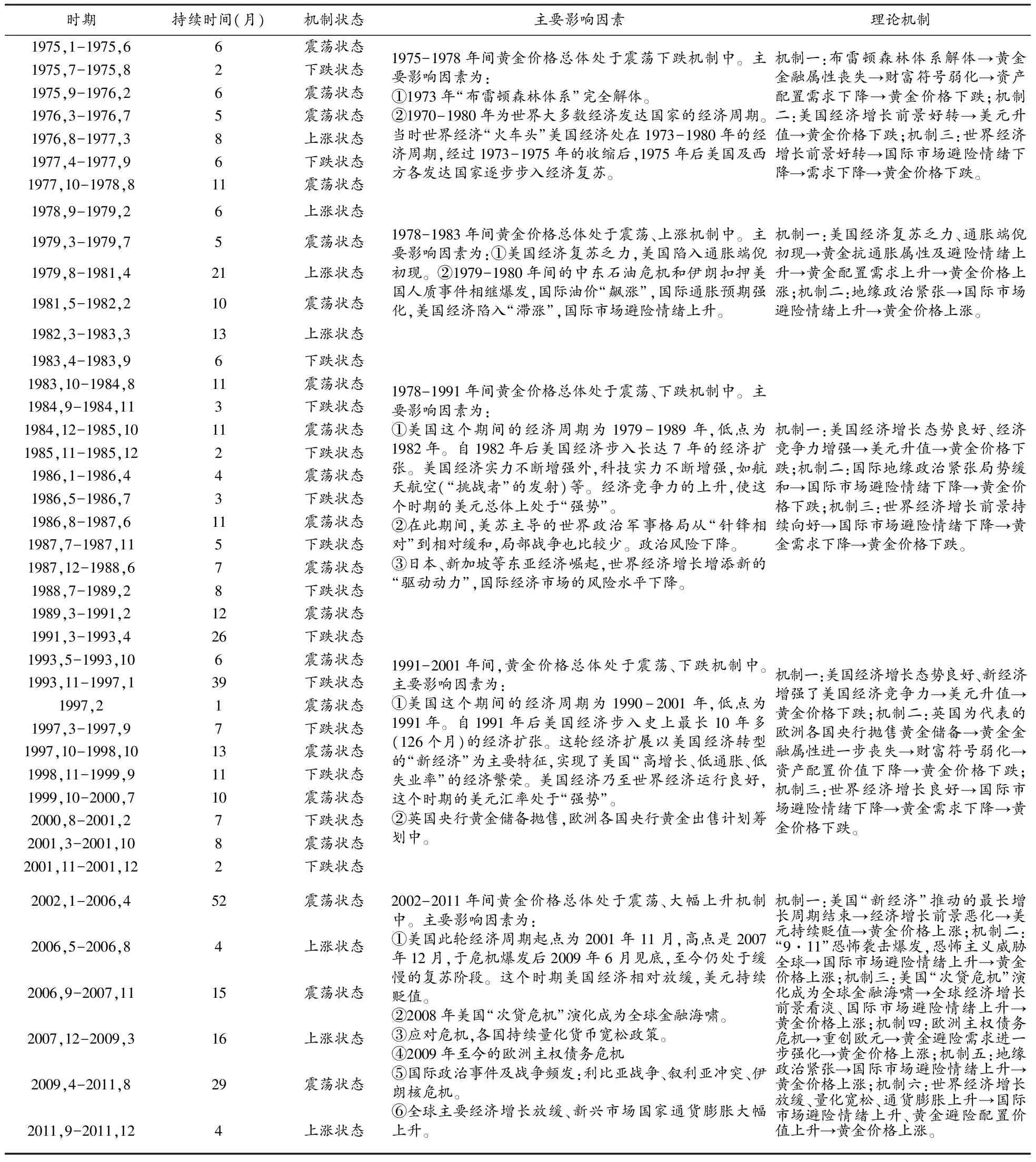
表2 黄金价格波动机制状态、主要影响因素与理论机制

资料来源：作者根据运算结果和相关资料整理

[1]Hamilton, James D. A new Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle[J].Econometrica,1989,(2).

[2]Myung Jig Kim, Charles R. Nelson, Richard Startz,Mean Reversion in Stock Prices? A Reappraisal of the Empirical Evidence[J].ReviewofEoonomicStudies,1991,(3).

[3]Bredin, Don and Stilianos Fountas. Inflation uncertainty, and Markov regime switching heteroskedasticity: evidence from European countries[J].Mimeo,2006,(4).

[4]谢赤，刘潭秋.人民币实际汇率中的马尔可夫转换行为[J].统计研究,2003,(9).

[5]赵留彦,等.中国通货水平与通胀不确定性: 马尔可夫域变分析[J].经济研究,2005,(8).

[6]魏巍贤,陈智文,王建军.三状态马尔可夫机制转换模型研究——在世界油价波动分析中的应用[J].财经研究,2006,(6).

[7]刘金全,刘志刚,于冬.我国经济周期波动性与阶段性之间关联的非对称性研究[J].统计研究,2005,(8).

关于我刊办公地址变更的通告

因我校校区整体搬迁，自2013年7月15日起，我刊办公地址变更为：浙江省杭州市余杭区仓前街道海曙路58号，邮编311121，编辑部电话号码、邮箱及网页不变。特此通告。

StudyonGoldPriceCyclicalFluctuationBasedonMarkovSwitchingModel

YAN Zhi-hui

(Assets Management Division, Shenyin & Wanguo Securities CO., LTD, Shanghai 200031, China)

The gold price fluctuations have become increasingly frequent since the 1970s. This paper studies the characteristics of gold price fluctuation during 1975-2011 based on the Markov switching model.The study found that: 1)the volatility of the price of gold is located in the different regions (up, horizontal shock, down); 2)the average duration of the three regions appears diferent; and 3)the regions of gold price fluctuations are caused by many factors, but the most important factor is the world economic situation, especially the U.S. Economy.

gold price cyclical fluctuation; Markov switching model; regional fluctuation characteristics

2012-09-05

浙江省高校人文社科重点研究基地课题“黄金及其衍生品组合投资研究” (RWSKZD01-201004)和浙江省哲学社会科学规划课题“浙江省外贸增长方式转变研究”(09CGYD039YBB)的研究成果。

严志辉(1974-)，男，浙江杭州人，经济学博士，讲师，申银万国证券股份有限公司客户资产管理总部高级研究员，主要从事包括大宗商品黄金资产等在内的各类证券投资产品的开发与创新。

F069

A

1674-2338(2013)04-0131-06

(责任编辑吴芳)