GM(1，1)与BP神经网络组合预测模型在田径成绩预测中的应用

郭维民

灰色系统理论自1982年问世以来，研究工作取得了很大的进展，已成功地应用于众多领域。GM(1，1)模型因其计算简便、实用广泛而在灰色预测中占有重要地位，是应用最早也是迄今为止应用最为广泛的灰色模型。灰色系统GM(1，1)模型是微分方程的时间连续模型，它将表面上无规律的原始数据变换成较有规律的生成数据后再建模。由于该模型不受一般统计模型对原始数据种种要求的约束，因而具有适应性强、预测性能好的优点。

本文首先给出灰色GM(1，1)模型的建模方法，然后考虑用BP人工神经网络算法对模型进行改进，建立灰色GM(1，1)与BP神经网络的组合预测模型。实例表明，相对于GM(1，1)模型用组合模型预测的精度预测有所提高。

1 研究对象与方法

1.1 研究对象

(1)第22～30届奥运会历届女子铅球冠军成绩;(2)我国链球运动员毕忠1989—1997年的链球比赛成绩。

1.2 研究方法

1.2.1 文献资料法 通过查阅相关文献资料，了解灰色模型和神经网络的建模方法，得到相关成绩数据序列。

1.2.2 建模法 首先介绍了GM(1，1)模型和GM(1，1)与BP神经网络组合预测模型的建模方法，然后针对第22届至第30届奥运会历届女子铅球冠军成绩和我国链球运动员毕忠1989—1997年的链球比赛成绩，各自分别建立了GM(1，1)模型和GM(1，1)与BP神经网络组合预测模型。

1.2.3 预测法 依据所建立的两种预测模型计算相关预测值。

1.2.4 检验法 比较预测值与实际成绩值，检验二者有无差异性。若有差异，分析差异程度如何。

2 模型建立与结果分析

2.1 建立灰色GM(1，1)模型

灰色GM(1，1)模型是最常用的单变量一次累加生成预测模型，其建模步骤及预测过程可归纳为:

(1)确定预测指标(变量)序列

若间距 Δki=ki－ki－1≠ ＜⊂≥∨⊆，则称 X(0)为非等间距序列;若间距Δki=const，则称X(0)为等间距序列。

(2)计算1次累加生成数据序列(1－AG0)

其中

(3)构造累加矩阵B

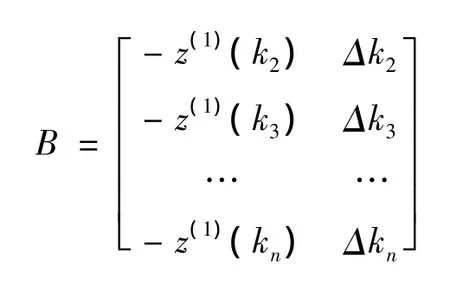
其中

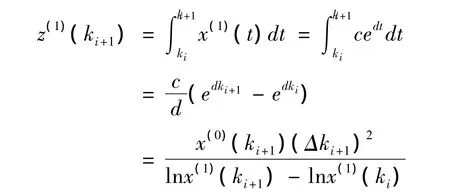
(4)利用最小二乘法则求^φ

其中

(5)建立预测模型方程并进行预测

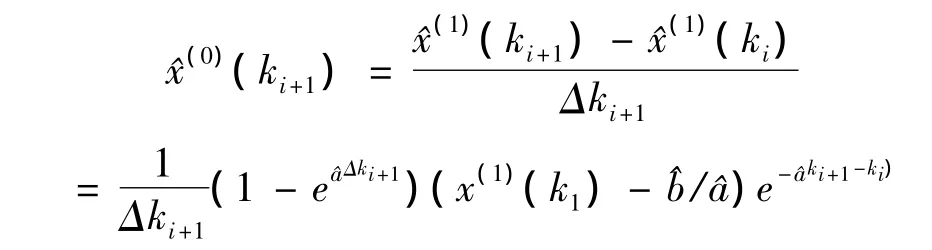
若个数据间的时间间隔是相等的，即Δki=const=Δk，则模型可以简化为

灰色预测具有要求样本数据少、原理简单、运算方便、短期预测精度高、可检验等优点，因此得到了广泛的应用，并取得了令人满意的效果。但是，它也存在着一定的局限性:GM(1，1)模型主要适用于单一的指数增长的模型，对序列数据出现异常的情况很难加以考虑，即必须进行模型预测结果的检验。因此，下面考虑用BP神经网络算法对GM(1，1)模型进行一定程度的改进。

2.2 建立GM(1，1)与BP神经网络组合预测模型

在对原始数据列建立GM(1，1)模型后，可得到对原始序列数据的一系列预测值。这些预测值可能和原始数据有一定的变差，而这些偏差关系可统一到神经网络模型中考虑[7]:将预测值作为神经网络的输入样本，实际值作为神经网络的输出样本，采取一定的结构，然后对神经网络进行训练，就可以得到一系列对应于相应节点的权值与阈值。将GM(1，1)各模型对下一时刻或多个时刻的预测值作为神经网络的输入，得到相应的输出值即为下一时刻或多个时刻最终的预测值。

这种组合方法，主要是通过三层BP神经网络(具有偏差)和至少一个S型隐含层加上一个线性输出层的网络能逼近任何有理函数的特性，通过训练使得神经网络来模拟序列数据之间的关系。假设某数据列有n个数据，组合模型预测步骤如下:

(1)对原始数据列建立GM(1，1)模型;

(2)用所建GM(1，1)模型预测数据列的第2到第n个数据，得到长度为n－1的数据序列P;

(3)取原始数列第2到第n个数据，得到另一个长度为n－1的数据序列T;

(4)将数列P作为神经网络的输入向量，T作为输出向量，训练BP网络，得到网络中对应于每个节点的一系列权值与阈值;

(5)再次用(1)中所建立的GM(1，1)模型来预测未来时刻(如n+1时刻)的值，并将预测值作为网络的输入向量，进行仿真，得到相应的输出向量，即GM(1，1)与BP神经网络组合预测模型的结果。

2.3 实例运用与结果分析

田径运动是一个明显的灰色系统。田径项目如短跑、中长跑、竞走、跳高、跳远、撑杆跳、铅球、铁饼、标枪、链球等这些比赛项目成绩可以认为是完全取决于运动员自身的身体素质和实力即个人发挥。相比体操、跳水等这些体育项目来说受评委主观评价较小，因此选用田径成绩进行模型的应用与检验更能检验模型的合理性及预测精度。

对成绩的预测分为两种，一种是根据某体育项目一段时间的成绩序列来预测下一时刻或多个时刻的成绩;另外一种是根据某运动员在某体育项目中的成绩序列来预测他在下一时刻或多个时刻的成绩。下面以第22届至第30届奥运会历届女子铅球冠军成绩为例进行第一种预测(见表1)，以我国链球运动员毕忠的历年成绩为例进行第二种预测(见表1、表2)。

文献[8]分别对GM(1，1)模型和 BP神经网络两种预测方法进行了比较，得出了灰色模型的预测精度远远高于神经网络模型的结论。而本文中由表1、表2的预测数据来看，GM(1，1)与BP神经网络组合模型相对于GM(1，1)模型的预测精度有很大提高，这说明了组合模型的可行性和准确性。

表1 第30届奥运会女子铅球冠军成绩两种模型预测精度比较

表2 链球运动员毕忠1997年比赛成绩两种模型预测精度比较

3 结论

本文建立的GM(1，1)与BP神经网络组合预测模型，采用灰色模型对数据序列进行预测，然后利用神经网络对预测值加以校正，得到最终预测值。与单纯用GM(1，1)模型进行预测相比，组合预测模型提高了预测的精度。非等间距灰色GM(1，1)模型可适用于非等间距序列进行灰色预测，提高了GM(1，1)模型的拟合精度，同时它也具有GM(1，1)模型预测精度高、所需样本少、计算简便等优点，进一步拓宽了GM(1，1)模型的应用范围。组合模型将GM(1，1)模型预测值与实际值之间的偏差关系统一到神经网络模型中来考虑，在利用神经网络对预测值加以校正时，采用的是BP神经网络。BP神经网络已被证明具有很强的模式识别能力或在任意精度内逼近任意连续映射的能力。这样使得模型具有更高的预测精度。

但是由于GM(1，1)模型是一种指数增长模型，使用灰色神经网络组合预测模型时，首先要用模型进行基于原始数据的预测，实际中用于预测的原始数据不一定会按指数形式规律变化。因此对于这些数据，其预测精度不能令人满意，使用范围也受到了限制，这也是GM(1，1)与BP神经网络组合预测模型的一个改进方向。另外，由于GM(1，1)模型预测所需数据量少，若数据增多，其预测精度会受到影响。因此当用该模型预测产生了多个数据后，再进行预测时应该考虑把原来的一些旧数据加以剔除，这样就更能反映新数据的变化趋势并提高精度。

[1]李春雷.2008年奥运会田径成绩预测及中国田径备战目标与对策研究[J].北京体育大学学报，2008，31(3):408 ～410.

[2]刘嘉津.解决转折期体育事件预测问题的GM(2，1)建模方法应用研究[J].天津体育学院学报，2006，21(3):252 ～254.

[3]闻新，周露，等.MATLAB神经网络应用设计[M].北京:科学技术出版社，2000.

[4]王钟羡，吴春笃，史雪荣.非等间距序列的灰色模型[J].数学的实践与认识，2003(10):16～20.

[5]郭存芝，汤瑞凉.应用非等时空距GM(1，1)拟合地下水计算参数[J].河海大学学报，1999，27(1):85 ～88.

[6]彭运福.灰色预测——校正模型及应用[J].系统工程，1989(3):37～41.

[7]许秀莉，罗键.一种新的组合灰色神经网络预测模型[J].厦门大学学报，2002，41(2):164 ～167.

[8]庄冲，王宗平.灰色系统模型与BP神经网络模型在体育成绩预测方面的比较研究[J].南京体育学院学报，2006，20(6):134～135.

[9]范文杰，刘芳.GM(1，1)模型在田径成绩预测中的运用[J].渝州大学学报，2001，18(3):63 ～66.

[10]韩中庾.数学建模方法及其应用[M].北京:高等教育出版社，2005.