无线传感器网络中的近似Unit Delaunay功率控制算法

徐鹏飞，陈志刚，邓晓衡

(1.湖南师范大学 数学与计算机科学学院，湖南 长沙 410081；2.中南大学 信息科学与工程学院，湖南 长沙 410083；3.湖南师范大学 高性能计算与随机信息处理省部共建教育部重点实验室，湖南 长沙 410081)

1 引言

传感器节点通过携带能量有限的电池供电，节能是无线传感器网络(wireless sensor network)设计的首要问题[1]。无线传感器网络功率控制在确保网络连通的前提下，兼顾通信干扰和网络延迟等设计目标，通过减小发射功率来降低节点的能耗，是延长网络生存周期的有效策略[2]。

无线网络的功率控制属于NP难问题，一般使用近似解决方案[2～4]。文献[3]将NP难的功率控制转换为协作路由，所有节点使用相同的发射功率；文献[4]提出节点自适应调整发射功率，建立协作路由的代价太大。文献[5]提出基于节点度的功率控制，每个节点调整发射功率使邻居维持在一个阈值内，不能保证网络的连通性。文献[6]提出基于方向的功率控制，每个节点调整发射功率使每个扇区ρ内至少有一个邻居，文献[7]证明ρ≤2π/k时满足k-连通，要求每个节点配备方向性天线，不适合廉价、微型的传感器节点。基于邻近图的功率控制使用邻近图作为无线网络的底层逻辑拓扑，从理论上保证网络拓扑的连通、逻辑邻居有界及延迟性能上界等[2,8]。UDel图(unit delaunay triangulation)是一种理想的无线网络邻近图，满足连通、对称、平面(planar)及t-支撑(t-spanner)等特性，不能分布式构造[8～11]；其中t-支撑是衡量网络延迟性能上界的重要指标[8]。若无特别说明，本文的图是指网络拓扑。

对于随机部署的无线网络，每个节点依据邻居构造的 Delaunay三角剖分(即 LDel图)非常接近UDel图，不过含有非对称和相交的边[9～11]；LDel图对称化和平面化后仍有可能满足 t-支撑，如PLDel图(planar local delaunay graph)[9]和 RDG 图(restricted delaunay graph)[11]。文献[11]构造RDG图的通信开销为 O(n2)，文献[12]优化后降为O( n)。文献[9]构造PLDel图的通信开销为O(n)，文献[13]优化后降低不明显。文献[14]提出与RDG图等价的Almost Delaunay图，其构造通信开销为O(n)，稍大于PLDel图。文献[10]提出与PLDel图等价的AUDel图(augment unit delaunay triangulation)，其构造通信开销约为PLDel图的50%。上述这些满足t-支撑的近似UDel图都是UDel图的超图。

此外，还可以从 UDel图的子图研究近似 UDel图，如RNG图(relative neighbor graph)、GG图(gabriel graph)和 PDT(partial delaunay triangulation)[15]图等；在分布式构造上述这些子图时，每个节点只要通过消息交互维护邻居的位置信息[15]，适合资源受限的传感器节点。遗憾的是，RNG图与GG图不满足t-支撑[8]，PDT图没有被证明满足t-支撑[15]；言外之意，上述这些UDel图的子图在网络延迟方面，很难满足无线传感器网络功率控制的设计目标。

针对基于邻近图的无线传感器网络功率控制，本文提出一种新几何结构AUDT (approximate unit delaunay triangulation)图，为无线传感器网络建立一个满足连通、对称、平面、逻辑邻居有界及t-支撑等特性的底层逻辑拓扑，每个节点依据最远的逻辑邻居调整到最小发射功率。本文工作的优势:AUDT图为 UDel图的子图，满足 t-支撑；分布式构造AUDT图的通信开销已经达到最小；AUDT图的网络延迟与UDel图和AUDel图相当，而最小发射功率与通信干扰均小于UDel图和AUDel图。

2 问题描述

在本文后继讨论中，将无线传感器网络作为平面上n个位置互异的节点集S，并假设任意4个节点不共圆以及所有节点不共线。

2.1 预备知识

1) 通信半径 R。所有节点具有相同的最大发射功率，节点在最大发射功率下的通信距离记为通信半径R。

2) 邻居集N(u)。相互位于通信半径R范围内的任意2个节点互为邻居或相邻；节点u∈S以及其所有邻居的集合记为邻居集N(u)，即k∈N(u)当且仅当||uk||≤R。

3) t-支撑[8～10]。用无向边连接任意 2个相邻节点，初始网络简化为一个连通的UDG图(unit disk graph)；UDG图的子图G满足t-支撑当且仅当任意节点 u 和 k 有||∏G(u,k)||≤t||∏UDG(u,k)||，其中||∏H(u,k)||是图H中连接节点u和k的最短路径长度；常数t(≥1)称为图G的t-支撑因子。

4) Voronoi划分[16]。将平面上的每个点划分到节点集 S中与之最近的节点，构成节点集 S的Voronoi划分 Vor(S)；其中，所有与节点 u∈S最近的点是一个凸多边形区域，记为 Voronoi区域V(S,u)；Voronoi区域的边界简称Vor边，每条Vor边为2个Voronoi区域共享的公共边界，如图1(a)所示。当V(S,u)和V(S,k)共享Vor边时，该Vor边位于线段uk的垂直平分线上。

5) UDel图[9]。任意节点 u、k∈S在 UDel图有一条无向边(记为UDel边uk)，当且仅当||uk||≤R且V(S,u)和V(S,k)共享Vor边。

引理 1 以点 q∈V(S,u)为圆心和||qu||为半径的圆内不包含S的任意节点[16]。

引理2 如果存在经过节点u、k∈S的圆C内不含S的任意节点, 则V(S,u)和V(S,k)共享Vor边，且圆C的圆心位于该Vor边上[16]。

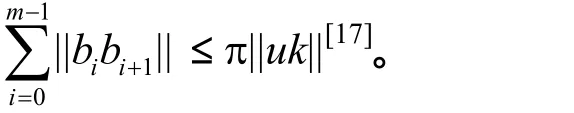
图1 Voronoi划分与DT(u,k)

2.2 AUDT图

定义1 (AUDT邻居)给定节点u的邻居k，如果 V(N(u),u)和 V(N(u),k)共享的 Vor 边上存在一个点与节点 u的距离≤R/2，则节点 k为节点 u的AUDT逻辑邻居，简称AUDT邻居。

定理 1 (对称性) 如果节点 k为节点 u的AUDT邻居，则节点u亦是节点k的AUDT邻居，即节点u和k互为AUDT邻居。

证明 依据定义1，设V(N(u),u)和V(N(u),k)共享Vor边ϖ的点q满足||qu||≤R/2，即q∈V(N(u),u)；依据引理1，以点q为圆心和||qu||为半径的圆Cq内不含N(u)的任意节点。Vor边ϖ在线段uk的垂直平分线上，点q∈ϖ满足||qk||=||qu||≤R/2，圆Cq的直径≤R且经过节点k和u，圆Cq在以节点u为圆心和R为半径的圆Cu内，如图2所示；显然，S-N(u)的所有节点在圆Cu外，圆Cq内不含S-N(u)的任意节点。因此，圆Cq内不含S的任意节点，当然圆Cq内不含N(k)的任意节点；依据定义1有||uk||≤R，将有k、u∈N(k)；依据引理2，圆Cq的圆心q在V(N(k),k)和V(N(k),u)共享的Vor边上；又知||qk||≤R/2，依据定义1，节点u为节点k的AUDT邻居。证毕。

图2 定理1的证明

定义2 (AUDT图) 任意节点u、k∈S在AUDT图有一条无向边(记为AUDT边uk)，当且仅当节点u和k互为AUDT邻居；所有AUDT边的集合构成一个对称的AUDT图。

3 AUDT功率控制

下面首先给出AUDT功率控制的算法描述，然后对算法进行理论分析。

3.1 算法描述

依据定义2，分布式构造AUDT图等价于每个节点求解AUDT邻居。当所有节点不共线时，Vor边为线段或半直线[16]；将半直线的无限远处抽象为虚拟点，任意Vor边简化为两点间的线段[18]。给定节点u的邻居 k，即 k∈N(u)(≠u)，设 V(N(u),u)和 V(N(u),k)共享Vor边k1k2，其中k1和k2分别为Vor边的2个端点。那么，Vor边k1k2与线段uk将满足下列情况之一。

1) Vor边k1k2与线段uk相交，如图3(a)所示。节点 k∈N(u)满足||uk||≤R，Vor边 k1k2又在线段 uk的垂直平分线上，那么线段uk的中点o满足o∈k1k2和||uo||=||uk||/2≤R/2，依据定义1，节点k为节点u的AUDT邻居。

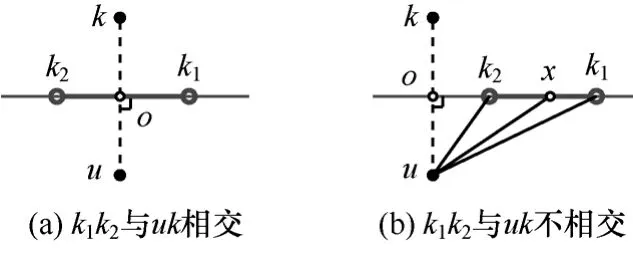
图3 Vor边k1k2与线段uk

综合上述，节点u求解AUDT邻居k仅使用Vor边k1k2；文献[18]的算法ICVR构造Voronoi区域 V(N(u),u)时，用 V(N(u),u)(k)(k2←k1)描述 V(N(u),u)和V(N(u),k)共享的Vor边k1k2。因此，AUDT功率控制的算法描述如图4所示，其中最小通信半径Rm为节点在最小发射功率下的通信距离。

图4 AUDT功率控制算法描述

3.2 理论分析

定理2 (时间复杂度)每个节点求解AUDT邻居的平均时间复杂度为O(Δ)，其中Δ为邻居数。

证明 图4初始化时，构造Voronoi区域的平均时间复杂度为O(Δ)[18]；For循环体为线性操作，任意Voronoi区域的Vor边平均数≤6[16]，For循环的平均时间复杂度为O(1)，即每个节点求解AUDT邻居的平均时间复杂度为O(Δ)。证毕。

定理3 (通信开销)构造AUDT图的通信开销为O(n)，其中n为节点数。

证明 图4初始化时，为了维护邻居的位置信息，每个节点广播自己的位置信息；For循环依据Vor边求解AUDT邻居，不需要交互任何信息，即每个节点求解 AUDT邻居时广播 1个消息，构造AUDT图的通信开销为O(n)。证毕。

定理4 (平面性) AUDT图是UDel图的平面子图，即满足平面性。

证明 已知 UDel图是一个平面图[9]。任意AUDT边uk，依据定理1的证明，存在经过节点u、k∈S的圆Cq内不含S的任意节点，V(S,u)和V(S,k)共享Vor边(引理2)。依据定义1，AUDT边uk满足||uk||≤R。综合上述，将有 UDel边 uk，即任意AUDT边亦是UDel边，当然AUDT图为UDel图的平面子图。证毕。

定理 5 (逻辑邻居有界)每个节点的平均AUDT邻居数≤6，即满足平均逻辑邻居有界。

上述6个系统也可以归纳到子功能包图范畴，以“资产报废处置管理系统”为例，它的主要目标就是帮助后勤仓库管理人员进行资产报废申请提交与资产报废功能启用，它主要会提出有关资产报废处置管理的4个子包，分别为资产报废申请、资产报废、报废资产启用以及审批。通过上述4个子包应用过程，就可以将报废固定资产系统工作再划分为报废申请与报废申请维护两部分，其中审批子包又可以分为对报废申请固定资产的审批以及对报废固定资产重新启用的审批［2］。

证明 给定 n个节点的 UDel图，其边数≤3n−6[9]；AUDT 图是 UDel图的子图(定理 4)，AUDT图的边数≤3n-6，每个节点的平均AUDT邻居数≤(3n−6)*2/n≈6。证毕。

推论1 对任意UDel边uk, DT(u,k)是AUDT图中连接节点u和k的路径。

证明 设 DT(u,k)=b0b1…bm-1bm，其中 b0=u和bm=k。任意0≤i＜m，依据引理3，设 V(S,bi)和V(S,bi+1)共享的 Vor边ϖi与线段 uk交于点 qi，将有qi∈V(S,bi)、qi∈uk 与 qi∈ϖi，如图 1(b)所示。

依据引理 1，以点 qi∈V(S,bi)为圆心和||qibi||为半径的圆Ci内不含S的任意节点，当然圆Ci内不含N(bi)的任意节点以及节点u和k；圆心qi满足qi∈uk，圆 Ci的直径在线段uk上，即 2||qibi||≤||uk||；UDel边 uk满足||uk||≤R，将有||qibi||≤R/2。Vor边ϖi在线段bibi+1的垂直平分线上，点qi∈ϖi满足||qibi||=||qibi+1||和||bibi+1||≤2||qibi||≤R，将有圆 Ci经过节点 bi和 bi+1以及 bi、bi+1∈N(bi)。

综合上述，经过节点bi、bi+1∈N(bi)的圆Ci内不含 N(bi)的任意节点，圆心 qi在 V(N(bi),bi)和V(N(bi),bi+1)共享的 Vor边上(引理 2)，且满足||qibi||≤R/2；依据定义 1和定理 1，节点 bi和 bi+1互为AUDT邻居，即有AUDT边bibi+1。因此，DT(u,k)的任意边亦是AUDT边，DT(u,k)是AUDT图中连接节点u和k的路径。证毕。

定理6 (t-支撑) AUDT图满足t-支撑，其t-支撑因子为2.42π。

证明 设任意节点u和k在UDel图的最短路径∏UDel(u,k)=u0u1…um-1um，其中 u0=u和 um=k，即有 UDel边 uiui+1(0≤i＜m)。依据推论 1，对任意 UDel边 uiui+1(0≤i＜m)，DT(ui,ui+1)是 AUDT 图中连接节点 ui和 ui+1的路径；显然，所有路径 DT(ui,ui+1)构成AUDT图中连接节点u和k的路径，即AUDT图为连通图；依据引理3，||DT(ui,ui+1)||≤π||uiui+1||；那么，AUDT图中连接节点u和k的最短路径长度||∏AUDT(u,k)||满足

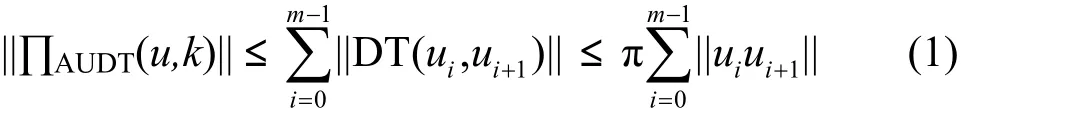
已知 UDel图满足 t-支撑，其 t-支撑因子为2.42[9]，即有

联立式(1)与式(2)有

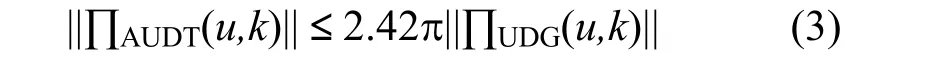
式(3)表明AUDT图满足t-支撑，其t-支撑因子为2.42π。证毕。

定理7 (连通性)AUDT图为连通图。

证明 依据定理6的证明可知。

4 仿真实验

为了评价算法性能，用 C++实现 AUDT图、AUDel图及UDel图，并进行大量仿真实验。在目标区域1000×1000内随机部署n个传感器节点，统计下列2组实验场景的最小通信半径、通信干扰、t-支撑因子及构造通信开销，所有结果均为 1000次仿真实验的平均值。

第1组:通信半径R设为50。在目标区域内随机部署1000个节点，然后每次随机增补200个节点，直到节点数量n增加到3000。

第2组:在目标区域内随机部署1000个节点。将通信半径R初值设为50，然后每次增加25，直到通信半径R增大到300。

4.1 最小通信半径

随着节点数量n的增加，更近的新邻居竞争为AUDT邻居，使AUDT图的最小通信半径Rm逐渐减小，即R/Rm呈下降趋势，如图5(a)所示。随着通信半径 R的增大，较远的新邻居竞争为AUDT邻居，使AUDT图的最小通信半径Rm逐渐增大，但R/Rm仍呈下降趋势，如图5(b)所示。与UDel图和AUDel图相比，AUDT图的最小通信半径减小1.1和1.3；随着节点数量n的增加，这种优势稍微有所减小；但随着通信半径R的增大，这种优势将越来明显。

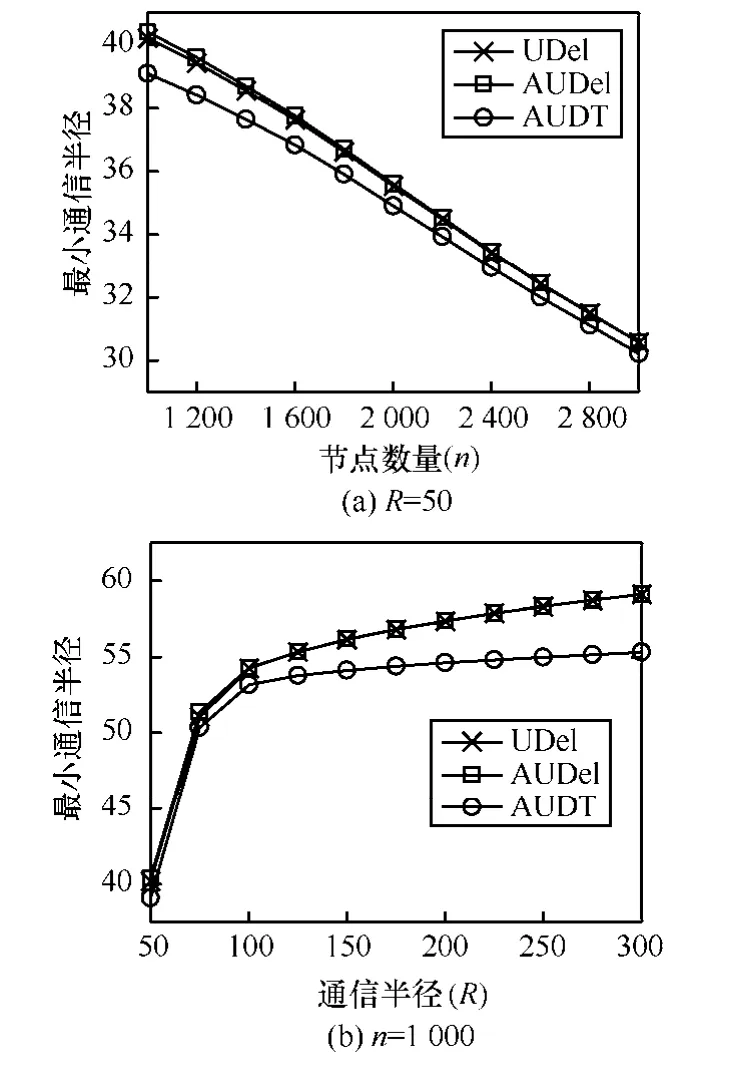
图5 最小通信半径

4.2 通信干扰

1) 随着节点数量n或者通信半径 R的增大，每个节点的平均AUDT邻居逐渐收敛于6，但不会超过6，如图6所示；大部分情况下，AUDT图的逻辑邻居，相对UDel图降低了0.16，相对AUDel图降低了0.19。

2) 物理邻居是指最小通信半径范围内的邻居。随着节点数量n的增加，虽然最小通信半径Rm减小(如图 5(a)所示)，但部署密度在增大，使 AUDT图的物理邻居逐渐增加，大致收敛于10，如图7(a)所示。随着通信半径R的增大，虽然部署密度不变，但最小通信半径Rm增大(如图5(b))，使AUDT图的物理邻居逐渐增大，维持在10左右，如图7(b)所示。与UDel图和AUDel图相比，AUDT图的物理邻居减少0.3和0.4；随着节点数量n的增加，这种优势稍微有所减小；但随着通信半径R的增大，这种优势越来明显。

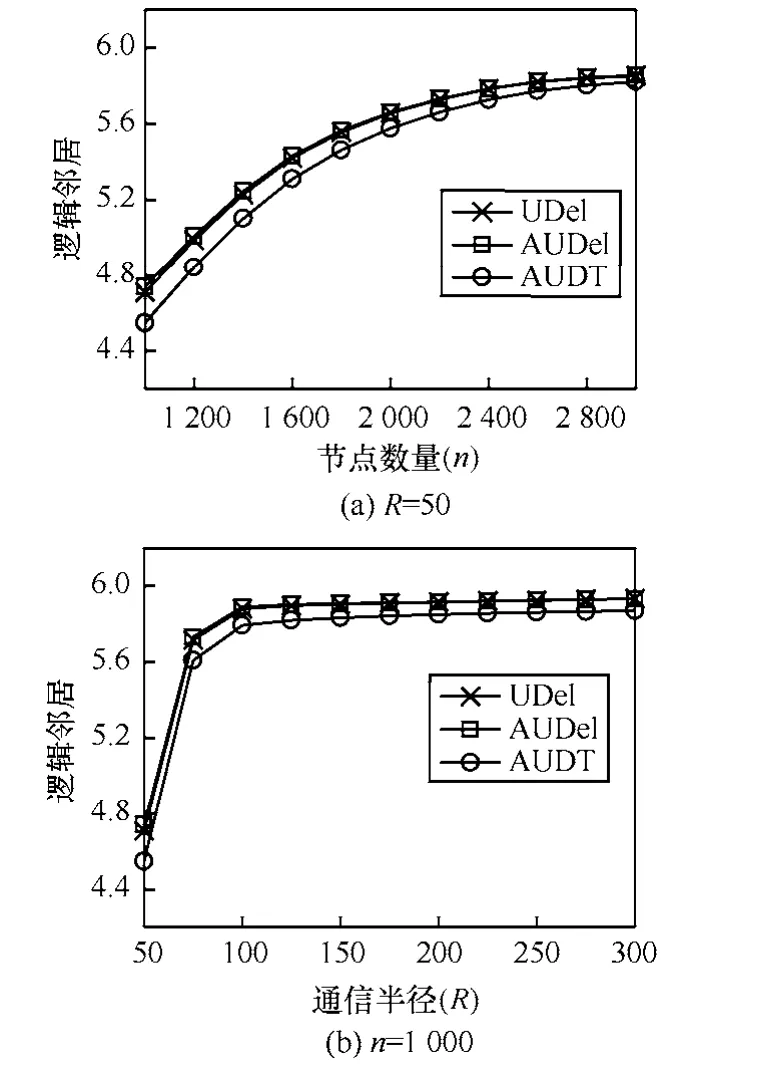
图6 逻辑邻居

图7 物理邻居

3) 通信干扰率=物理邻居/逻辑邻居。随着节点数量n的增加，AUDT图的通信干扰率逐渐增大，大致收敛于 1.7，如图 8(a)所示。随着通信半径 R的增大，AUDT图的通信干扰率逐渐增大，维持在1.7左右，如图8(b)所示。与UDel图和AUDel图相比，AUDT图的通信干扰率降低0.026和0.034；随着节点数量n的增加，这种优势有所减小；但随着通信半径R的增大，这种优势越来越明显。

图8 通信干扰率

4) 物理邻居和通信干扰率是衡量节点间通信干扰程度的重要指标[8]。总的来说，AUDT图的物理邻居维持在10左右，通信干扰率维持在1.7左右，明显小于UDel图和AUDel图，即AUDT图的通信干扰程度要小于UDel图和AUDel图。

4.3 t-支撑因子

理论上，UDel图和 AUDel图的 t-支撑因子为 2.42[9,10]，AUDT图的 t-支撑因子为 2.42π(定理6)。实际上，随着节点数量n或者通信半径R的增大，AUDT图的 t-支撑因子逐渐增大，大致收敛于1.126，稍大于UDel图和AUDel图，如图9所示。总的来说，AUDT图的t-支撑因子与UDel图和AUDel图之间的差别，随着节点数量n或者通信半径 R的增大逐渐减小，最大差值不超过0.022；即 AUDT图的网络延迟与 UDel图和AUDel图相当。

4.4 构造通信开销

本节的构造通信开销是指分布式构造无线网络邻近图时，每个节点平均广播的消息数量。AUDel图通过消息交互完成 LDel图的对称化和平面化，每个节点平均广播的消息数量维持在4左右，其中包含 1个广播自己的位置信息。在分布式构造AUDT图时，每个节点只要广播自己的位置信息，不到AUDel图的1/3，如图10所示，这已是分布式构造无线网络邻近图的最小通信开销。

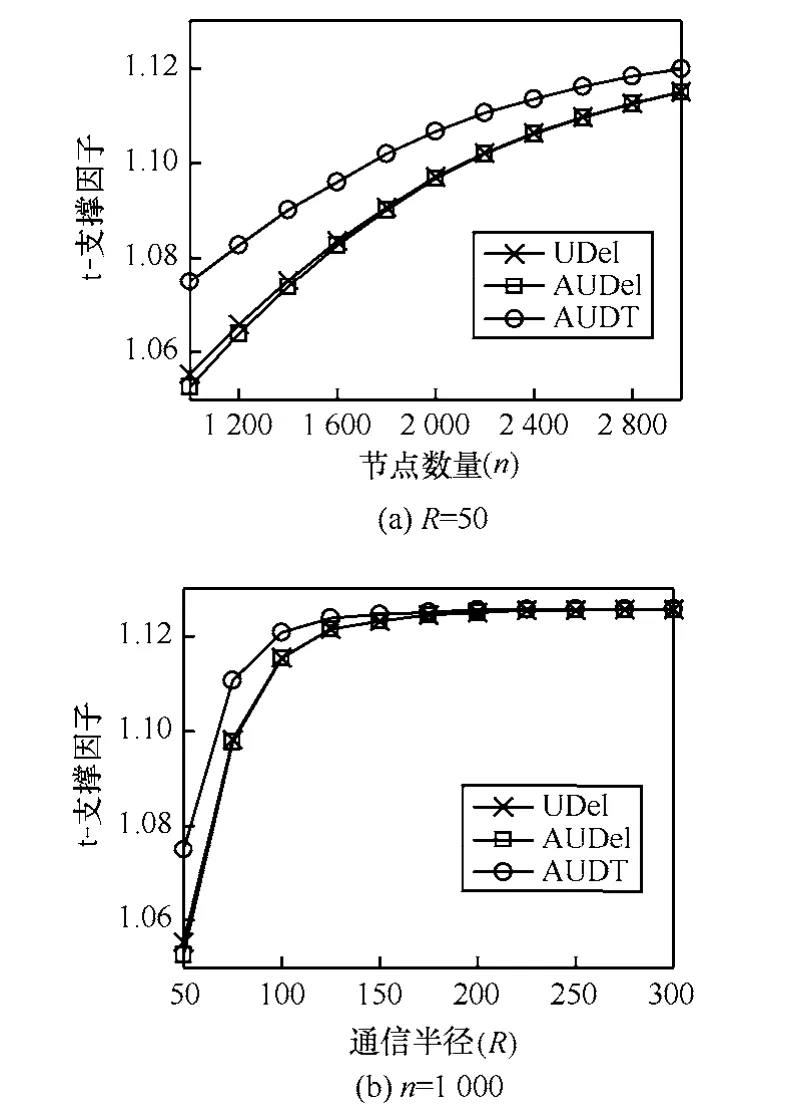
图9 t-支撑因子

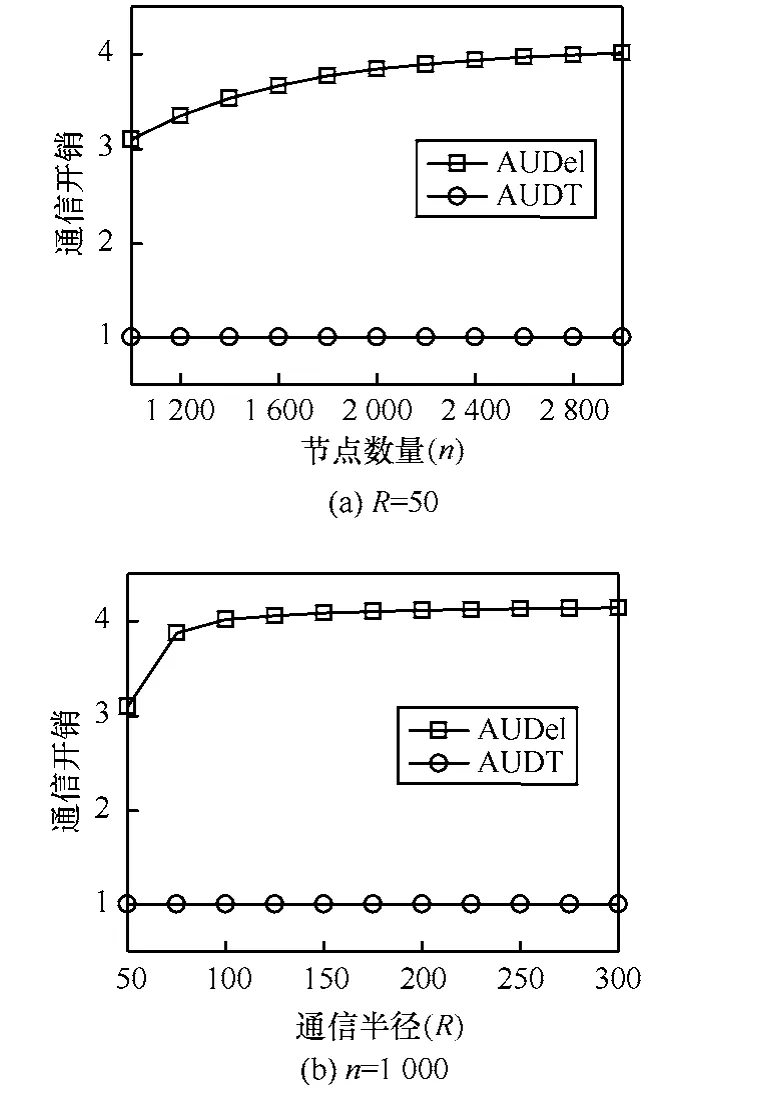
图10 通信开销

5 结束语

本文提出一种新几何结构 AUDT图以及其分布式构造算法，应用于无线传感器网络功率控制。理论证明 AUDT图满足连通、对称、平面、逻辑邻居有界及t-支撑等特性。仿真实验显示，AUDT图的网络延迟与 UDel图和 AUDel图相当，而最小通信半径与通信干扰(包括物理邻居与通信干扰率)均小于UDel图和AUDel图，特别是分布式构造 AUDT图的通信开销已经达到最小。下一步工作将考虑节点加入、退出及移动等情况，改进AUDT功率控制；AUDT图只考虑了平均逻辑邻居有界，下一步将约束每个节点的逻辑邻居数量；将 AUDT功率控制和睡眠调度结合，研究更为高效的拓扑控制机制等。

[1]ANASTASI G, CONTI M, FRANCESCO M D.Energy conservation in wireless sensor networks:a survey[J].Ad Hoc Networks,2009,7(3):537-568.

[2]张学, 陆桑璐, 陈贵海.无线传感器网络的拓扑控制[J].软件学报,2007, 18(4):943-954.ZHANG X, LU S L, CHEN G H.Topology control for wireless sensor networks[J].Journal of Software, 2007, 18(4):943-954.

[3]NARAYANASWAMY S, KAWADIA V.Power control in ad-hoc networks:theory, architecture, algorithm and implementation of the COMPOW protocol[A].Proc of European Wireless Conference[C].Florence, 2002.156-162.

[4]ZHANG X, LIU M, GONG H.PCAR:a power controlled routing protocol for wireless ad hoc networks[A].Proc of IEEE International Symposium on a World of Wireless Mobile and Multimedia Networks,Montreal[C].2010.1-16.

[5]KUBISCH M, KARL H.Distributed algorithms for transmission power control in wireless sensor networks[A].Proc of IEEE Wireless Communications and Networking[C].New Orleans, 2003.558-563.

[6]LI L, HALPERN J.A cone-based distributed topology-control algorithm for wireless multi-hop networks[J].IEEE/ACM Transactions on Networking, 2005, 13(1):147-159.

[7]PODURI S, PODURI S.Using local geometry for tunable topology control in sensor networks[J].IEEE Transactions on Mobile Computing,2009, 8:(2):218-230.

[8]路纲, 周明天, 牛新征.无线网络邻近图综述[J].软件学报, 2008,19(4):888-911.LU G, ZHOU M T, NIU X Z.A survey of proximity graphs in wireless networks [J].Journal of Software, 2008,19(4):888-911.

[9]LI X Y, CALINESCU G, WANG P J.Distributed construction of a planar spanner and routing for ad hoc wireless networks[A].Proc of IEEE INFOCOM[C].New York , 2002.1268-1277.

[10]李铭, 卢锡城, 彭伟.面向无线Ad Hoc网络的一种平面t-支撑图[J].通信学报, 2006, 26(6):62-69.LI M, LU X C, PENG W.Planar t-spanner for wireless ad hoc networks [J].Journal on Communications, 2006, 26(6):62-69.

[11]GAO J, GUIBAS J L, et al.Geometric spanners for routing in mobile networks[J].IEEE Journal on Selected Areas in Communications,2005,23(1):174-185.

[12]CHEN A.Fast and efficient restricted delaunay triangulation in random geometric graphs [J].Internet Mathematics, 2008, 5(3):195-210.

[13]FILIPE A, LUIS R.Single-step creation of localized delaunay triangulations [J].Wireless Networks, 2009, 15(7):859-873.

[14]HAIDER M B, IMAHORI S J.Success guaranteed routing in almost delaunay planar nets for wireless sensor communication[J].International Journal of Sensor Networks, 2011, 9(2):69-75.

[15]LI X Y, IVAN S.Partial delaunay triangulation and degree limited localized Bluetooth scatternet formation [J].IEEE Transactions on Parallel and Distributed Systems, 2004, 15(4):350-361.

[16]MARK D B, OTFRIED C.Computational Geometry:Algorithms and Applications (3rd) [M].Berlin Heidelberg:Springer-Verlag, 2008.

[17]DOBKIN D P, FRIEDMAN S J, SUPOWIT K J.Delaunay graphs are almost as good as complete graphs [J].Discrete Computational Geometry, 1990, 5(1):399-407.

[18]XU P F, CHEN Z G, DENG X H.An efficient implementation of incremental construction voronoi region [J].International Journal of Advancements in Computing Technology, 2012, 4(2):230-237.