关于有向环网平均直径的研究

陈业斌，李颖，郑啸，陈涛

（1.安徽工业大学 计算机学院，安徽 马鞍山 243002；2.马鞍山师范高等专科学校 理工系，安徽 马鞍山 243041）

1 引言

从目前网络运营商为大用户提供的光纤接入网状况来看，对于某些大型用户，比如电力、电信、有线电视等，其主干网大多以环型网络的方式提供服务。其中，比较有代表性的有电力通信系统的SDH（synchronous digital hierarchy）环网、电信系统的以太环网和有线电视光纤网。

全光通信技术的发展为环型网络在现实世界中的应用提供了可能和保障，环网的通信性能与其拓扑结构密切相关。一个结构不好的环网往往会出现信息传输延迟较大、通信效率和容错效率低下等现象。为了更好地发挥环网在各行业的潜力，必须在设计其结构时对其进行优化。

环网技术要达到应用级要求，高可靠性是首先需要解决的问题。网络的高可靠性与网络的传输延迟密切相关。传输延迟是指信号从一个地方传输到另一个地方所需的时间，是指信号传输的群延时，即信号以群速通过一个物理连接所经历的时间。在端到端通信连接中，产生延时的环节很多，主要是由传输媒质延时和网络节点延时组成。光在纤芯中传输速率很快，因此，与网络节点延时相比，传输媒质延时可以忽略不计。网络节点延时是指信号通过若干网络节点过程中的延时，这是造成信号传输延时的主要原因，这部分延时与传输距离无关，只与网络系统中的节点多少以及网络结构相关。

节点相同的环型网络，由于其结构上的差异，其传输延迟有时相差很大。因此，对网络结构的优化是一个比较重要的课题。以前人们往往用直径去度量传输延迟。直径可定义为任意 2个节点之间最短距离的最大值，而平均直径定义为任意2个节点之间最短距离的平均值。因此，人们自然会产生这样的疑问:就传输延迟而言，直径与平均直径哪个更具有代表性呢？直径最小的网络，其平均直径是否也是最小值呢？本文将以环型网络中的有向双环网络和有向三环网络为基础研究这个理论问题。

近年来，关于环型网络的研究主要集中在双环网络和三环网络上。研究的目标主要集中在网络直径、路由和构造最优网络和容错等问题上。Wong和 Coppersmith[1]证明了有向双环网络的直径存在下界，该结论为研究紧优有向双环网络提供了理论依据。Chen[2,3]证明了有向双环网络最小路径图的存在，并给出L-型瓦的定义。有了最小路径图，直径的计算变得更加容易。接下来，人们用数学的方法证明了大量紧优有向双环网络的存在[4～6]；方木云[7]用仿真的方法发现了大量紧优环网。2007年，GOMEZ[8]给出了有向双环网络的最优路由算法。有向双环网络能并行传输信息，为了衡量其并行传输能力，CHEN[9]给出了宽直径对其并行传输的效率进行度量。能够并行输送信息的网络一定具有容错能力，DHARMASENA[10]和陈业斌[11]分别给出了有向双环网络容错路由算法和容错容直径的计算方法。

就平均直径而言，人们对其认识和研究还不够深入，相关的结论也很少。2009年，方木云[12]对非单步长有向双环网络的平均直径进行了研究，给出了平均直径的计算公式:avg d(N;r,s)=从计算公式中不难发现，i从1变化到n−1只能得到n−1个 d，最后求平均值应该是除以 N−1，而不是除以N。当N的值较小时，其计算结果会存在较大的误差。2011年，边琼芳[13]也对双环网络平均直径进行了研究，但并没有得出新的结论。

本文针对环型网络这一较有代表性的网络结构，针对目前应用较为广泛的有向双环网络和有向三环网络，就其平均直径做如下研究。

1) 根据有向双环网络的最小路径图（L-型瓦），给出计算任意节点有向双环网络 G(N;r,s)平均直径的计算公式及算法。

2) 根据有向三环网络的最小路径图（T(N; s1, s2,s3)），给出计算任意节点有向三环网络平均直径的计算公式及算法。

3) 通过实验分析有向环型网络中直径与平均直径之间的关系，通过实验数据对比分析平均直径在有向环网传输效率上的代表性。

2 有向双环网络的平均直径

有向双环网络的拓扑结构是一个如图 1(a)所示的有向图G(N;r,s)，其节点数N不小于4，r和s为网络的步长，而且满足关系式:1≤r ＜s ＜N（r,s为整数）[1]。L-型瓦是有向双环网络的最小路径如图 1(b)所示。L-型瓦通常是由 a、b、p和 q 4个参数所决定的L型区域（矩形为其特例），其中，a、b、p和 q都是整数，且 a,b≥2，0≤p＜a，0≤q＜b，记为L(N; a,b,p,q)[1]。当双环网络的3个参数N、r、s的最大公约数为1，即gcd(N;r,s)=1时，有向双环网络为一个强连通图，下文中的研究都是在强连通图的基础上进行的。

定义1 对于任意给定N（N≥4）的有向双环网络G(N;r,s)，当r取某大于0的整数值，且满足r＜ s ＜ N，s从r到N−1之间变化所得到的一组有向双环网络称为有向双环网络的一个无限族。

图1 G(12;2,5)的拓扑结构及其L-型瓦

定义 2 有向双环网络的直径是指在有向双环网络中，任意2点之间最短距离的最大值，表示为 d(N;r,s)=max{du,v, (0≤u ≠ v≤N−1)}，其中，du,v指节点u到节点v的最短距离。

定义3 有向双环网络的平均直径是指在有向双环网络中，一个节点到其他所有节点最短距离的平均值，表示为(N;r,s)=(0≤i ≠ j≤N−1)，其中，di,j指节点 i到节点 j的最短距离。

2009年，方木云[12]对非单位步长的平均直径进行了研究，他的算法思想是在生成有向双环网络最小路径图—L-型瓦的过程中，利用相关参数来计算平均直径，该算法的时间复杂度最高为 O(N2)。为了提高效率，本文将采用新的算法，无需绘制 L-型瓦，只要知道G(N; r, s)中的N、r和s的值，就能计算出L-型瓦的4个参数a、b、p和q，从而计算出有向双环网络的平均直径。

2.1 平均直径的计算公式

研究表明:在有向双环网络中，与距离相关的问题都可以利用有向双环网络的最小路径图—L-型瓦来得到[8]。根据有向双环网络直径的定义，则d(N; r, s)=max{a+b−q−2, a+b−p−2}。有向双环网络的平均直径(N; r, s)也可以从L-型瓦中得到，有向双环网络的平均直径可以用 L-型瓦的 4个参数表示，如定理1所描述。

定理 1 令有向双环网络的最小路径图表示为L (N; a, b, p, q)，则其平均直径(N;r,s)可分为2种情况。

证明 将 L-型瓦看作是由若干个单元格所组成的，每一个单元格放一个节点。因为有向双环网络的L-型瓦总体可分为2种情况:当ab=N时，L (N;a, b, p, q)为矩形；当 ab ＜ N 时，L (N; a, b, p, q)为“L”型。根据有向双环网络 G(N;r,s)的对称性，节点u到节点v之间的距离等于节点0到节点v−u之间的距离，所以要研究有向双环网络中的平均距离，只要考虑L(N; a,b,p,q)中节点0到其他节点的平均距离。

1) 当ab=N时，p=q=0，此时，平均直径d(N;r,s)可以看成是节点 0到剩下 N−1个节点距离的平均值。由于相连2个节点的距离为1，所以节点0到其他N−1个节点的平均距离为

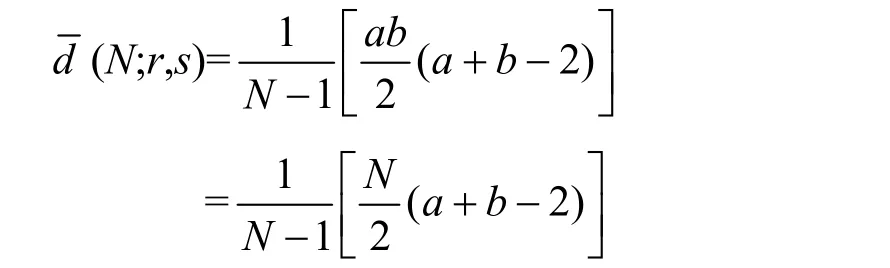
2) 当ab＜N时，设节点0到边长为a和b的大矩形的每个单元格的距离之和为φ，设节点0到边长为p和q的小矩形的每个单元格的距离之和为δ，则有

2.2 计算平均直径的算法

根据有向双环网络平均直径的计算公式，要计算G(N;r,s)的平均直径，必须先计算出L (N; a, b, p,q)的4个参数。为此给出2种直接计算L-型瓦4个参数的算法，当有向双环网络 G(N;r,s)的第一步长r=1时，使用算法1；否则使用算法2。

算法1 递归算法。

该算法的实现过程如下。

1) 令 l−1=N，l0（0≤l0≤N）为正整数且满足:rl0+s≡0(mod N)；定义 li、qi为如下的递归式:li−2=qili−1+li(0≤li≤li−1, 1≤i≤m+1, lm+1=0)。

2) 定义 U−1=0，U0=1 且 Ui+1=qi+1Ui+Ui−1(0≤i≤m)。由定义可知li随着i的增大不断减小，直到lm+1=0为止；Ui随着i的增大不断增大，直到Um+1=N为止，于是有

4) L-型瓦的 4个参数分别为:a=lu−vlu+1，b=Uu+(v+1)Uu+1，p=lu−(v+1) lu+1，q=Uu−vUu+1。

5) 根据定理1计算d(N;r,s)。

算法2 同余方程算法。

该算法的实现过程如下。

1) 解同余方程:a=min{j|ks=jr(mod N), j ＞ k≥0, j=2,…,N−1}，q={k|ks=ar(mod N), k≥0}。算法思想是设计一个双重循环，外循环j从2到N−1变化，内循环k从1到j−1变化，当ks(mod N)=jr(mod N)时，a=j，q=k。

2) 解同余方程:b=min{k|ks=jr(mod N), k≥j≥0, k=2,…,N−1}，p={j|bs=jr(mod N), j≥0}。算法思想是设计一个双重循环，外循环k从2到N−1变化，内循环j从1到k−1变化，当ks(mod N)=jr(mod N)时，b=k，p=j。

3) 根据定理1计算d(N;r,s)。

3 有向三环网络的平均直径

与有向双环网络相比，有向三环网络系统中的每个节点都多出一条有向边，这无疑给实际的系统增加了成本，同时也增加了技术难度。人们之所以关注它，是因为与相同节点的有向双环网络相比，有向三环网络的信息传输延迟相对较小，尤其是当节点数较大时更是如此。那么随着节点数和边数的增加，环型网络的平均直径又会发生怎样的变化呢？下面将以有向三环网络为代表，来研究其平均直径的相关特性，并与有向双环网络的相关数据进行比较。

有向三环网络的图论模型是一个如图2所示有向图G(N; s1,s2,s3)[14]，其中，N、s1、s2和s3都是自然数，且满足:N≥4，1≤s1≠ s2≠ s3＜ N。图中有 N个节点，分别记为 0,1,2,…,N−1，有 3个步长，分别记为s1、s2和s3，每个节点v发出3条有向边:v→v+s1(mod N)、v→v+s2(mod N)和 v→v+s3(mod N)，分别记为[+s1]边、[+s2]边和[+s3]边。对于一个给定的 N、s1、s2、s3的有向三双环网络，其平均直径是一定的。

现有的研究结果表明:超L-型瓦结构是三环网络所对应的最小路径图之一[15]，它是一个三维立体图形[16]，当网络节点较大时，仿真试验的效率不是很理想，其相关参数的计算比较复杂。2002年，侯新民等提出了利用图层的方式来研究三环网络[17]，该思想与超L-型瓦相比，虽然复杂度上大大降低了，但其只限于第一步长为单位步长的有向三环网络，并不具有通用性。研究表明:利用树型结构来研究有向环网，可使研究工作相对简单化[18]。本文将有向三环网络的空间结构映射为二维平面上的三叉树结构，并证明三叉树结构是有向三环网络最小路径图的另一种表现形式。在此基础上，进一步对三环网络的平均直径相关特性进行研究。

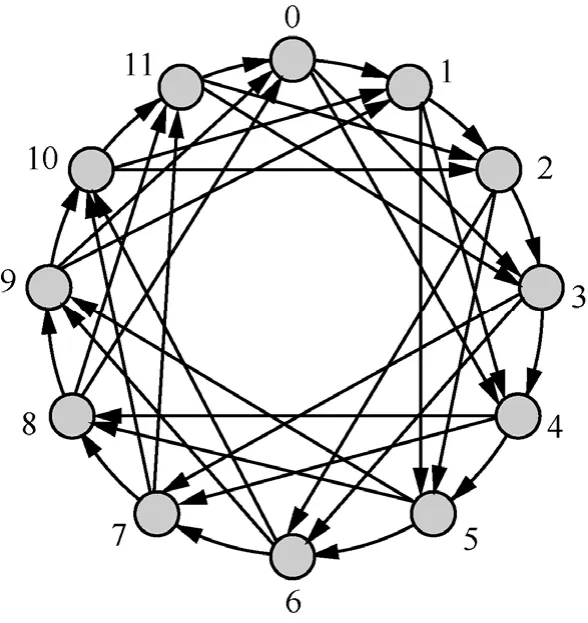
图2 有向三环网络G(12;1,3,4)的拓扑结构

3.1 构建最小路径图

定义4 对于任意给定N（N≥4）的有向三双环网络G(N;s1,s2,s3)，当s1和s2取大于0的整数值，且满足 s1＜s2＜N，s3从 s2到 N−1之间变化；或当s1=1，s3=N−1，s2从s1到s3之间变化，所得到的一组有向三环网络称为有向三环网络的一个无限族。

定义 5 三环网络的直径是指在三环网络中，任意2点之间最短距离的最大值，表示为d(N; s1, s2,s3)=max{du,v, (0≤u ≠ v≤N−1)}，其中，du,v指节点u到节点v的最短距离。

定义 6 三环网络的平均直径是指在三环网络中，一个节点到其他所有节点最短距离的平均值，表示为(N;s1,s2,s3)=(0≤i≠j≤N−1)，其中，di,j指节点i到节点j的最短距离。

由定义5和定义6可知，不论是计算有向三环网络的直径还是平均直径，都必须求出有向三环网络中任意2节点之间的最短距离，但从图2所示的拓扑结构中显然无法直接求出任意2节点之间的最短距离。为此，将三环网络的拓扑结构映射为二维平面上等价的三叉树结构，得到三环网络的最小路径图。其映射方法如定义7。

定义7 有向三环网络的等价树T (N;s1,s2,s3)的构造方法如下。

1) 选节点0为三叉树的根节点，其所对应的层数为第0层。

2) 分别以[+s1]边、[+s2]边和[+s3]边为连线，以s1、s2、s3的值来构造三叉树第1层上的节点。

3) 分别取第i（i≥1）层上的每一个节点v，分别以[+s1]边、[+s2]边和[+s3]边为连线，以v+ s1(mod N)、v+s2(mod N)、v+s3(mod N)的值来构造三叉树第i+1层上的节点；若新的节点在三叉树中已经出现，则第i+1层上不再放置该节点。

4) 重复步骤3)，直到三叉树中不再出现新的节点为止。

定义7所生成的图形是一个三叉树结构，有向三环网络 G(12;1,3,4)所对应的三叉树 T(12;1,3,4)结构如图3所示。

图3 三叉树T(12;1,3,4)

定义8 若有向三环网络G(N;s1,s2,s3)中的所有节点都在其等价的三叉树T(N;s1,s2,s3)中出现，则称此三叉树为满节点树。

满节点树出现的充要条件是图 G(N;s1,s2,s3)为强连通图，此时N、s1、s2、s3必须满足条件:gcd(N, s1,s2, s3) =1，即N、s1、s2、s34个数的最大公约数为1。下文所做的研究都是在满节点树的基础上展开的。

根据有向三环网络的对称性，任意节点x到节点y之间的距离等于节点0到节点y − x(x＜y)之间的距离。因此，研究三环网络的相关问题，只需研究节点0到其他任意节点之间的相关问题。所以在三叉树的根节点上放置了节点 0。于是，三环网络的直径可以重新表示为:d(N;s1,s2,s3)=max{d0,v,(0＜v≤N−1)}，平均直径可以重新表示为:(N;s1,s2,s3)=(1≤i≤N−1)。

3.2 平均直径的计算策略

研究表明:有向三环网络的最小路径图可以表示为三叉树结构，其平均直径为三叉树中根节点到其他节点的平均距离。其依据如下。

引理1 从三叉树T(N;s1,s2,s3)的根节点(节点0)出发，必存在一条路径p=m[+s1]+n[+s2]+k[+s3](m≥0, n≥0, k≥0，m、n、k不全为0)可以到达树中的任意节点 v(v ≠ 0)。

证明 由定义7可知，除第0层外，其他层上的节点至少存在一个父节点，而它们共同的祖先是根节点(节点 0)，因此从根节点可以到达任意节点v(v ≠ 0)。由于树中的任意节点 v(v ≠ 0)的值都必须满足同余方程:v=ms1+ns2+ks3(mod N) (m≥0, n≥0,k≥0)，所以必存在一条从根节点到节点v(v ≠ 0)的路径p, 且p=m[+s1]+n [+s2]+k [+s3](m≥0, n≥0, k≥0，m、n、k不全为0)。

引理2 在三叉树T(N;s1,s2,s3)中，从根节点出发经过路径p（p=m[+s1]+n [+s2]+k [+s3]）到达任意节点v(v ≠ 0)的路径长度Lp=m+n+k，且Lp为2节点间最短路径的长度。

证明 由三环网络 G(N;s1,s2,s3)的拓扑结构可知，从节点0到任意节点v(v ≠ 0)都存在多条路径。由引理1可知，在三叉树T(N;s1,s2,s3)中，必存在一条路径p=m[+s1]+n[+s2]+k[+s3](m≥0, n≥0, k≥0，m、n、k不全为0)，使得从根节点出发经过路径p到达树中任意节点v，其路径p的长度为Lp=m+n+k。假定树中存在路径p '，使得从根节点出发经过路径p'到达节点 v，其路径长度 Lp'＜Lp，则节点 v 应该出现在更小的层上，后面的层上就不会再出现节点v。现在是在2层上都现出了节点v，这与定义7矛盾，假设不能成立。所以在树T(N;s1,s2,s3)中，从根节点出发经过路径p到达节点v的路径长度Lp为根节点到任意节点v的最短路径长度。

定理2 在三叉树T(N;s1,s2,s3)中，节点v的层数l等于其最短路径长度Lp。

证明 由引理 2可知，在等价树 T(N;s1,s2,s3)中，根节点到任一层上节点v的路径长度Lp等于其到节点v的最短路径长度。令v=ms1+ns2+ks3(mod N) (m≥0, n≥0, k≥0，m、n、k不全为 0)，则最短路径长度为 Lp=m+n+k。由定义 7可知，在树T(N;s1,s2,s3)中，若节点v=ms1+ns2+ks3(mod N)，则从根节点开始共走m+n+k步到达v，而每走一步，层数就会增加一层，因此，节点 v所位于的层数l=m+n+k。于是得:节点v的层数l等于其最短路径长度Lp。

定理 3 三叉树 T(N;s1,s2,s3)是三环网络 G(N;s1,s2,s3)所对应的最小路径图。

证明 由定理2可知，在三叉树T(N;s1,s2,s3)中，节点v的层数l等于其最短路径长度Lp。因此，根节点到任一层上节点距离都相等，且为最短距离。由于在三叉树中不存在多余的重复节点，所以三叉树 T(N;s1,s2,s3)是三环网络 G(N;s1,s2,s3)所对应的最小路径图。

定理 4 有向三环网络的平均直径d(N;s1,s2,s3)等于其三叉树T(N;s1,s2,s3)的层数l与每层节点总数nl积之和的平均值。即(N;s1,s2,s3)=(1≤l≤L)。

证明 根据平均直径的定义和定理3可知，有向三环网络的平均直径可以看成是T(N;s1,s2,s3)中节点0到其他节点最短距离的平均值。首先，节点0到其他节点的路径数共有N−1条；其次，设三叉树T(N;s1,s2,s3)的层数l=1,2,3,…,L（L为最大层数），每层上的节点数为nl，则节点0到其他节点路径的总长度为，所以(N;s1,s2,s3)=

3.3 计算平均直径的算法

根据上文的分析可知，要计算有向三环网络G(N;s1,s2,s3)的平均直径，首先必须构造出相应的等价树，得到其层数以及每层上的节点个数。其算法如下。

1) 定义3个线性表l、l1和l2，线性表l中首先放节点0作为根节点，线性表l1放3个节点s1、s2和s3作为树的叶子节点，线性表l2置空。定义初始树高:layer=1。定义树中路径总长度初值:sum=3。

2) 依次取线性表 l1中的每个节点 v，以v+s1(mod N)、v+s2(mod N)和 v+s3(mod N)来生成 3个新的叶子节点，若每个新的节点在树中没有出现过，则分别将其加入到l1和l2中。然后将节点v从l1移到l中。

3) 判断线性表l2是否为空，若不为空，统计线性表 l2中叶子节点的个数放置到 k中，layer++，sum=sum+layer*k，将线性表l2置空，重复步骤2)，直到l2为空，即不再产生新的叶子节点为止。

4 实验结果及分析

1974年，Wong C K和Coppersmith D 给出了有向双环网络G(N;r,s)直径的下界:lb=−2[1],表示不小于x的最小整数。如果某G(N;r,s)的直径取得最小值，即d(N;r,s)=−2，则称该双环网络G(N;r,s)是最优双环网络。若最优环网的平均直径也取最小值，此时的环网从传输效率上来看应该是最优中的优秀者，因此，将其定义为双优网络。双优网络也应该存在三环网络的无限族中。

同一网络的直径与平均直径之间是否存在一定的关系？有向环网的平均直径是否可以代替直径来表示网络的传输效率？带着这些问题，笔者利用Java作为前台开发工具，SQL Server 2005作为后台数据库服务器，建立了有向环网仿真实验平台，对有向双环网络和三环网络多个无限族进行了大量的实验，实验参数选取如下。

1) 节点数N是从4～1000中抽取出的一系列整数，其中，4～1000区间中的每一个N值都必须进行实验，从1000～10000区间中取一个数作为起点（如1100），然后按循环变量加上某整数（如i+100）的数列选值。

2) 根据环网的对称性，有向双环网络的第一步长r的变化范围为1～N/2；第二步长s的变化范围为r～N−1。有向三环网络的第一步长s1选取为1，第二步长s2变化范围为1～N−2，第三步长s3选取为N−1。这样的取值可使得到的每一个无限族都很完整，容易发现数据的变化规律。

3) 存放到后台数据库中的参数有:节点值 N，步长r、s或（s1、s2、s3），直径d，平均直径d。

表1所示为有向双环网络G(50;1,s) 和有向三环网络G(50;1,s,49) 2组无限族的直径和平均直径的部分实验数据。为了简化表中数据，分别用、、)和(50)来替代)、d()和()。根据实验数据绘制的仿真图如图4和图5所示。

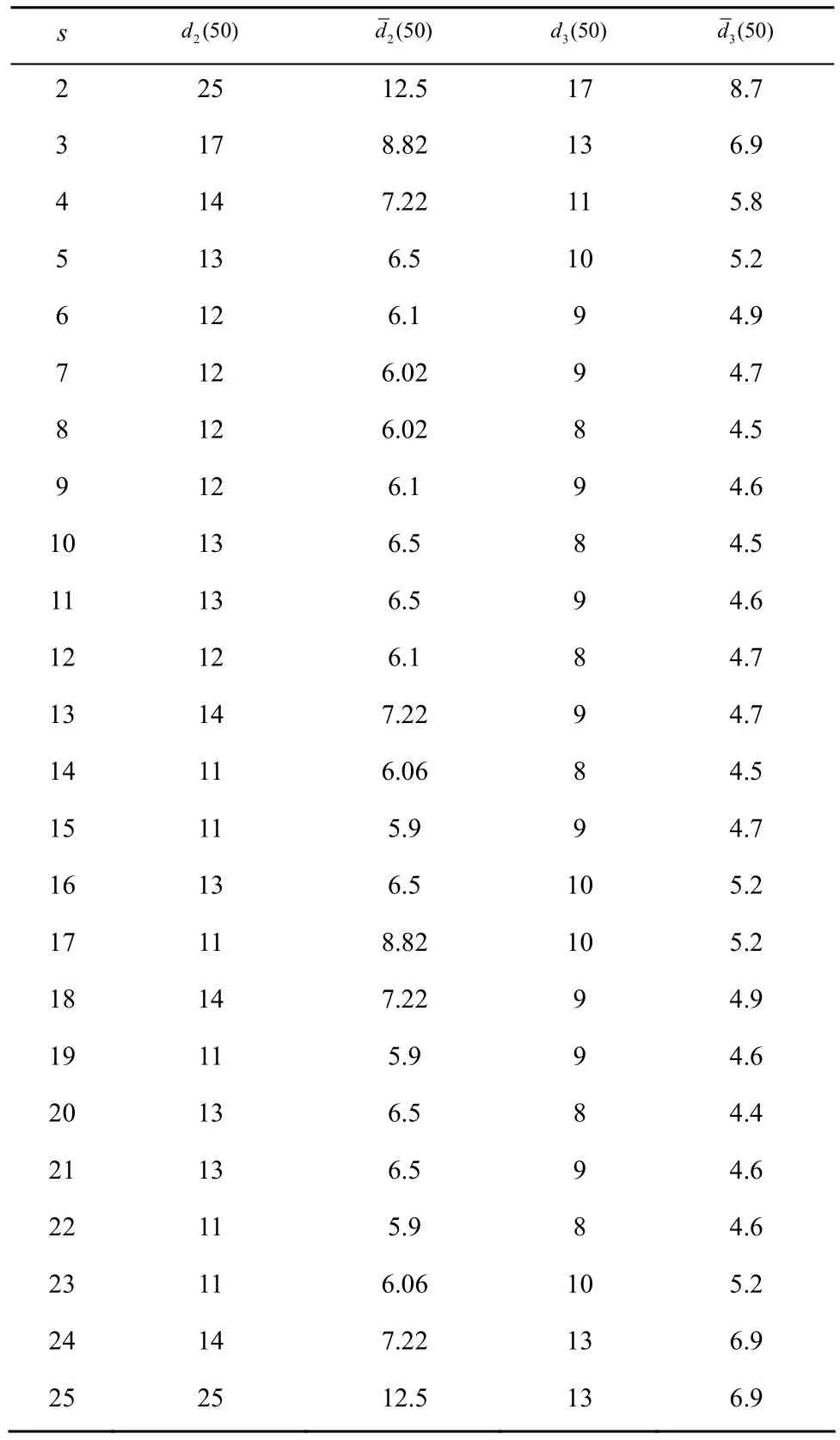
表1 G(50;1,s)和G(50;1,s,49)的直径和平均直径对照

表1中的数据包括有向双环网络G(50;1,s)的第二步长s在2～49变化所得的无限族中直径和平均直径的值，还包括有向三环网络G(50;1,s,49)的第二步长s在2～48变化所得的无限族中直径和平均直径的值。根据有向环网的对称性，只取前一半数据来分析即可。

对于有向双环网络 G(50;1,s)，其直径下界为lb=−2=−2=11，从表1中的数据可以看出 G(50;1,14)、G(50;1,15)、G(50;1,17)、G(50;1,19)、G(50;1,22)、G(50;1,23)的直径都是 11，达到了下界值，根据定义这些都是最优双环网络。进一步分析可知，在该无限族中，平均直径的最小值是5.9，对应的网络分别是 G(50;1,15)、G(50;1,19)、G(50;1,22)。由此可见:平均直径最小的有向双环网络一定是最优的，反之不然。另外，最优有向双环网络的平均直径之间存在较大的差值:(50;1,17)−d(50;1,15)=8.82−5.9=2.92。从表中数据还可以看出相同有向双环网络的平均直径约等于直径的一半。

根据实验数据分析得:有向三环网络 G(N;s1,s2,s3)在 4≤N≤86的区间内满足:d(N;s1,s2,s3)≥−1，当N＞86时，其下界的分布是一个分段函数，目前还没能找到其分布规律。对于有向三环网络G(50;1,s,49)，其直径下界为lb=−1 =8，从表 1中的数据可以看出 G(50;1,8,49)、G(50; 1,10,49)、G(50;1,12,49)、G(50;1,14,49)、G(50;1,20,49)、G(50;1, 22,49)的直径都是8，达到了下界值，它们都是最优网络。进一步分析可知，在该无限族中，最小的平均直径为d(50;1,20,49)=4.4。由此可知:平均直径最小的有向三环网络一定是最优的，反之不然。从表中数据还可以看出有向三环网络的平均直径约等于其直径的一半。

图4所示为有向双环网络无限族G(50;3,s)的直径与平均直径的分布，图5所示为有向三环网络无限族G(50;1,s,49)的直径与平均直径的分布。从图4和图5中可以看出:不论有向双环网络还是有向三环网络，在一个无限族内，直径和平均直径的分布都呈轴对称图形；在一个无限族内，直径到达下界的网络个数往往要大于平均直径达到最小值的网络个数；在一个无限族内，平均直径的变化规律与直径大致相同，但又不完全相同。

图4 G(50;1,s)无限族的直径和平均直径的分布

图5 G(50;1,s,49)无限族的直径和平均直径的分布

5 结束语

通过对有向环网平均直径的研究，笔者发现同一网络的平均直径与直径之间存在着一定的关系:同一网络的平均直径约等于直径的一半；在一个无限族中，当某网络的直径取得最小值时，其平均直径不一定取得最小值，有时甚至相差很多；但平均直径最小的网络其直径一定也取最小值，此时的网络传输效率是最高的，因此，称此类网络为双优网络。以前在设计网络结构时，通常只是用直径的大小作为传输效率的衡量标准，研究表明就传输效率而言，平均直径比直径更具有参考价值。因此，平均直径应该成为构造环型网络重要的参考依据之一。

有向双环网络的直径存在下界，有向三环网络的直径在一定的区间范围内也存在下界。那么，有向环网的平均直径是否也存在下界呢？它的存在对计算平均直径的最小值有着一定的意义，这将成为下一个要攻克的难题。

[1]WONG C K, COPPERSMITH D.A combinatorial problem related to multimodule organizations[J].J Assoc Computer, 1974, 21(3):392-402.

[2]CHEN C Y, HWANG F K.The minimum distance diagram of double-loop networks[J].IEEE Transactions on Computers, 2000, 49(9):977-979.

[3]CHEN C Y, JAMES K L, TANG W H.An efficient algorithm to find a double-loop network that realizes a given L-shape[J].Theoretical Computer Science , 2006, 359(1-3):69-76.

[4]AGUILO F, FIOL M A.An efficient algorithm to find optimal double loop networks[J].Discrete Mathematics,1995,138(1-3):15-29.

[5]CHEN B X, XIAO W J.Optimal designs of directed double-loop networks[A].Lecture Notes in Computer Science (LNCS)[C].Berlin,Germany:Springer Verlag, 2004.19-24.

[6]周建钦.关于 K紧优双环网络[J].中国科学技术大学学报, 2005,35(6):738-742.ZHOU J Q.On K-tight optimal double-loop networks[J].Journal of University of Science and Technology of China, 2005,35(6):738-742.

[7]方木云,赵保华,屈玉贵.双环网络G(N;1,s)的L形瓦仿真算法[J].系统仿真学报.2005, 17(4):914-916.FANG M Y, ZHAO B H, QU Y G.An algorithm to simulate the L-shaped tile of double-loop networks G(N;1,s)[J].Journal of System Simulation, 2005,17(4):914-916.

[8]GOMEZ D, GUTIERREZ J, IBEAS A.Optimal routing in double loop networks[J].Theoretical Computer Science, 2007, 381(1-3):68-85.

[9]CHEN Y B, LI Y, WANG J K.On the wide diameter of directed double-loop network[J].Journal of Network and Computer Applications,2011, 34(2):692-696.

[10]DHARMASENA, HETTEHE P, XIN Y.An optimal fault-tolerant routing algorithm for weighted bidirectional double-loop networks[J].IEEE Transactions on Parallel & Distributed Systems, 2005, 16(9):841-852.

[11]陈业斌,王建堃,李颖.有向双环网络的容错路由及容错直径[J].华中科技大学学报(自然科学版),2010,38(2):12-15.CHEN Y B, WANG J K, LI Y.Fault-tolerant routing and diameters of directed double-loop networks[J].Journal of Huazhong University of Science and Technology (Natural Science Edition), 2010,38(2):12-15.

[12]方木云, 汤红霞.非单位步长双环网络平均直径的研究[J].华中科技大学学报(自然科学版), 2009,37(6):12-15.FANG M Y, TANG H X.A survey on the average diameter of double-loop networks with non-unit step[J].Journal of Huazhong University of Science and Technology (Natural Science Edition), 2009,37(6):12-15.

[13]边琼芳,姜太平,刘辉等.双环网络平均直径的研究[J].安徽工业大学学报(自然科学版),2011,28(3):277-281.BIAN Q F, JIANG T P, LIU H, et al.Survey on the average diameter of double-loop networks[J].J of Anhui University of Technology(Natural Science), 2011,28(3):277-281.

[14]AGUILO F, FIOL M A, GARCIA C.Triple-loop networks with small transmission delay[J].Discrete Math, 1997,15(4):3-16.

[15]CHEN C Y, HUNG C S, TANG W S.On the existence of hyper-L triple-loop networks[J].Discrete Math, 2006,306(12):1132-1138.

[16]邰伟鹏,方木云,徐宏.三环网络 TL(N;1,s,s+1)超 L-型瓦仿真算法[J].华中科技大学(自然科学版), 2010,38(8):50-52.TAI W P, FANG M Y, XU H.Algorithm to simulate the hyper L-shaped tile for triple-loop networks TL(N;1,s,s+1)[J].Journal of Huazhong University of Science and Technology (Natural Science Edition), 2010,38(8):50-52.

[17]侯新民, 王天明.分布式三环网络传输延迟[J].大连理工大学学报,2002,42(1):9-12.HOU X M, WANG T M.On the transmission delay of distributed triple loop networks[J].Journal of Dalian University of Technology, 2002,42(1):9-12.

[18]陈业斌.基于二叉树的有向双环网络最短路径算法[J].华中科技大学学报(自然科学版), 2009,37(4):78-81.CHEN Y B.Bintree-based shortest path algorithm of directed double-loop networks[J].Journal of Huazhong University of Science and Technology (Natural Science Edition), 2009,37(4):78-81.