“形数”试题缤纷现 如今靓影又重来——对湖北省3道高考“形数”试题的赏析
2013-10-26
●
(黄陂区第一中学盘龙校区 湖北武汉 430312)
“形数”试题缤纷现如今靓影又重来——对湖北省3道高考“形数”试题的赏析
●李红春
(黄陂区第一中学盘龙校区 湖北武汉 430312)
翻开2013年湖北省数学高考试卷,一股别样的气息扑面而来,特别是理科第14题,该题融知识、方法、思想、能力于一体,文化底蕴深厚.值得一提的是这是湖北省自主命题以来,第3次考查“形数”知识,然而常考常新,不禁让人有这样的感慨:“形数”试题缤纷现,如今靓影又重来!
1 靓影重现
例1古希腊毕达哥拉斯学派的数学家研究过各种多边形数,如三角形数1,3,6,10,…,第n个三角形数为
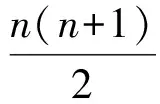
记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:

四边形数N(n,4)=n2;

六边形数N(n,6)=2n2-n;
……
可以推测N(n,k)的表达式,由此计算N(10,24)=______.
(2013年湖北省数学高考理科试题)
解法1 由观察可知

N(n,4)=1+3+5+…+(2n-1)=n2;
N(n,5)= 1+4+7+…+(3n-2)=
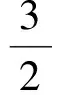
N(n,6)=1+5+9+…+(4n-3)=2n2-n;
…
N(n,k)= 1+(k-1)+(2k-3)+…+
[(k-2)n-(k-3)]=

从而
N(10,24)=1 000.
解法2由观察可知
N(n,k)=an2+bn.


从而
N(10,24)=1 000.
例2传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数,他们研究过如图1所示的三角形数:

图1
将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn}.可以推测:
(1)b2 012是数列{an}中的第______项;
(2)b2k-1=______(用k表示).
(2012年湖北省数学高考文科试题)
解归纳猜想数列{an}的通项公式为
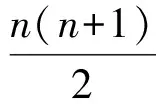
又数列{bn}是由可被5整除的三角形数按从小到大的顺序组成一个新数列,由任意2个连续正整数之积的个位数字特征可得:
b1=a4,b2=a5,b3=a9,b4=a10,
b5=a14,b6=a15,b7=a19,b8=a20,
…
归纳猜想,得
b2k-1=a5k-1,b2k=a5k,
从而
b2 012=b2×1 006=a5×1 006=a5 030,

例3古希腊人常用小石子在沙滩上摆成各种形状来研究数,比如:
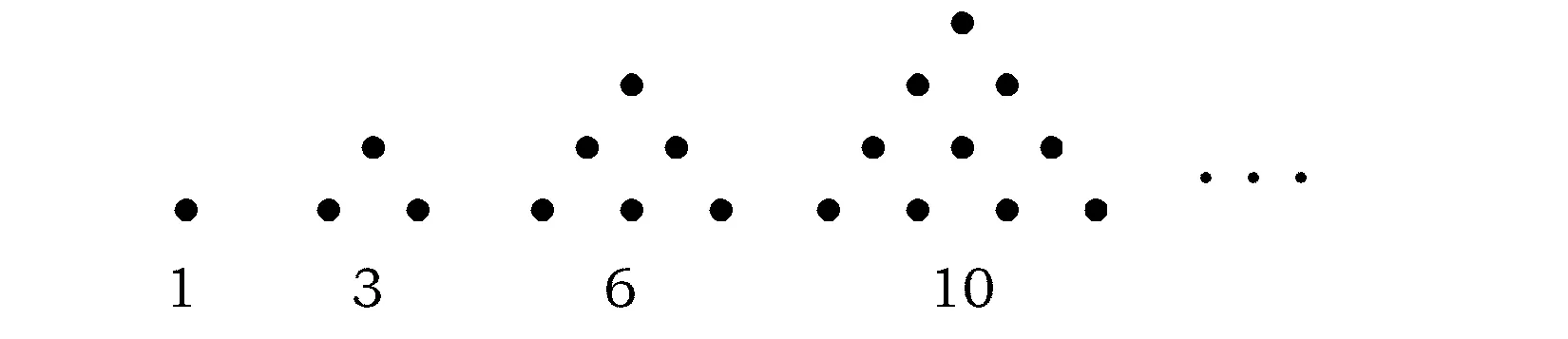
图2

图3
他们研究过图2中的1,3,6,10,…由于这些数能够表示成三角形,将其称为三角形数;类似地,称图3中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是
( )
A.289 B.1 024 C.1 225 D.1 378
(2009年湖北省数学高考理科试题)
解设三角形数数列为{an},观察图形可知a1=1,a2=3=1+2,a3=6=1+2+3,a4=10=1+2+3+4,猜想
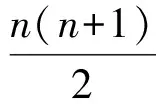
设正方形数数列为{bn},由b1=1=12,b2=4=22,b3=9=32,b4=16=42,猜想
bn=n2.
分析可知三角形数的个位数字只能是0,1,3,5,6,8.正方形数是平方数,其个位数字只能是0,1,4,5,6,9.故排除选项A,B,D,选C.
2 亮点赏析
2.1 植根课本
“问渠那得清如许,为有源头活水来”,以上3道试题均源自新课标人教A版《数学(必修5)》第2.1节“数列的概念与简单表示法”的引言部分以及《数学(选修3-1)》第2.2节“毕达哥拉斯学派”的部分内容.由于试题取材于课本,不但背景公平,而且学生做这样的试题倍感亲切,无形中加深了对课本的深厚感情,对引导师生重视课本、研读教材、挖掘教材有着重要作用.
2.2 底蕴深厚
著名数学家和数学史家邹腾强调:通过数学史的学习,学生不仅获得了一种历史感,而且通过从新的角度看数学学科,他们将对数学产生更敏锐的理解力和鉴赏力.
在数学史上,古希腊数学家毕达哥拉斯最早把正整数和几何图形联系在一起,把数描绘成沙滩上的小石子,又按小石子所能排列的形状,把正整数与正三角形、正方形等图形联系起来,将数分为三角形数、正方形数……
形数试题底蕴深厚,如三角平方数数列为{fn},则
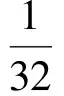
这个含有无理数的公式,给出的解却是正整数,与斐波纳契数列{an},其通项为
一样神奇.这些以数学史为背景的试题的出现,不但激发了人们对数学学习的兴趣,更在潜移默化中传播了源远流长的数学文化.
2.3 立意高远
合情推理,是数学家波利亚提出的概念,它是指“观察、归纳、类比、实验、联想、猜测、矫正和调控等方法”.一直以来,我们十分重视双基教学,但学生在校所学到的学科知识,随着他们离开学校,多数会逐渐忘掉.“教育是所有学会的东西都忘却以后仍然留下来的那些东西”,学生学习数学获得的不仅仅是知识,除此之外,更重要的是思想与方法.而在研究“探究性学习”的今天,我们的教学一直在研究如何组织和组织的形式上,对在发展过程中使用的合情推理等方法没有予以足够的重视,而这些恰恰是人类优秀文化素质的重要组成部分.归纳、类比是发现和获取知识的重要方法,也是探究和解决问题的重要工具,如今归纳与演绎并重已成为新课程数学教学的一条重要原则.我们的数学课堂,一方面要教会学生规范地演绎推理证明,另一方面也要教会学生运用归纳、类比、合情推理发现和猜想.《数学(选修2-2)》中专设一章推理与证明,结合具体案例进行学习和深化.
这3道“形数”试题,别具一格,着重考查学生合情推理能力,以及特殊与一般思想;考查考生探索、研究及理性思维.在此题的求解过程中,“归纳、猜想、验证,从特殊到一般”展现了数学命题的发现与验证的全过程,突出了新课程“知识与技能、过程与方法、情感态度与价值观”的三维目标.
2.4 导向鲜明
这3道试题取材一样,都是将文字语言和图形语言相结合,以数学符号语言和图形语言为载体,要求学生从特殊结构发现一般规律,提醒我们:高三复习必须重视对历年高考试题的研究!因为历年高考试题一直是新高考试题的重要来源,命题者一直重视传承和相互借鉴,他们坚持“命题是一种自然的发展,不会有突变,不能隔断历史”的观点.其次,高考试题凝结了命题者巨大的智慧和心血,有的立意高远,有的背景深刻,有的内涵丰富,有的创意新颖.在研究的过程中,我们可以掌握丰富的数学方法,学习朴素的数学原理,完成火热的数学思考,激发蕴藏的生命活力,使我们领悟解题方法、解题思想、问题的深层次联系,使我们的解题能力与思维品质向更深、更高的层次发展和升华!
