历经三重境界探究椭圆性质的一个案例

● ●

(宁波市第二中学 浙江宁波 315000) (鄞州区教育局教研室 浙江宁波 315100)

历经三重境界探究椭圆性质的一个案例

●任伟芳●江一鸣

(宁波市第二中学 浙江宁波 315000) (鄞州区教育局教研室 浙江宁波 315100)

高中数学课程标准指出：“高中数学课程应力求通过各种不同形式的自主学习、探究活动，让学生体验数学发现和创造的历程，发展他们的创新意识．”笔者在备高三复习课时，发现一个探究椭圆性质的题目，通过此题可以引导学生从一个普通数学问题出发，层层推进，自主探索，合作交流，进而领悟数学思想方法．为此，笔者以该题为引子精心编制了一个“探索椭圆的一个性质”的教学设计，并在教研活动中进行了展示，获得广泛好评．下面是这堂探究课的教学片断和课后思考，供大家参考．

1 教学片段实录

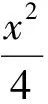
(2009年辽宁省数学高考理科试题)

说明课前预习作业要求：(1)用尽可能多的证法来证明；(2)如果移动点A会改变直线EF的斜率，那么直线EF的斜率与点A的哪个值有关；(3)能否把这个结论推广到抛物线和双曲线上.

片段1不畏浮云遮望眼,只缘身在最高层

师：预习作业同学们准备得很充分，4位同学分别用直接法、方程组法、参数法和点差法来证明，这4种证法都很精彩．尽管题目像“雄关漫道真如铁”，同学们还是用多种解法把它“从头越”．现在我们已处在题目思路方法的“最高层”，但不要被“浮云遮望眼”，力图抓住问题的本质，去猜想、拓展、引申和类比，探究出新的问题．想一想：直线EF的斜率值与点A的哪个值有关系？

生1：直线EF的斜率与过点A的椭圆切线斜率是互为相反数．我是用量角器通过量直线的倾斜角验证得到的，但是还没有证明出来．

生2：这个结论我是猜想得出．

师：你是怎样猜想出来的？

生2：只要把如图2的椭圆变成特殊情形圆，如图1所示，∠1=∠E+∠4，∠2=∠3+∠5，而∠1=∠2，因此∠4=∠5.类比到图2得：直线EF的斜率与过点A的椭圆切线斜率是互为相反数．

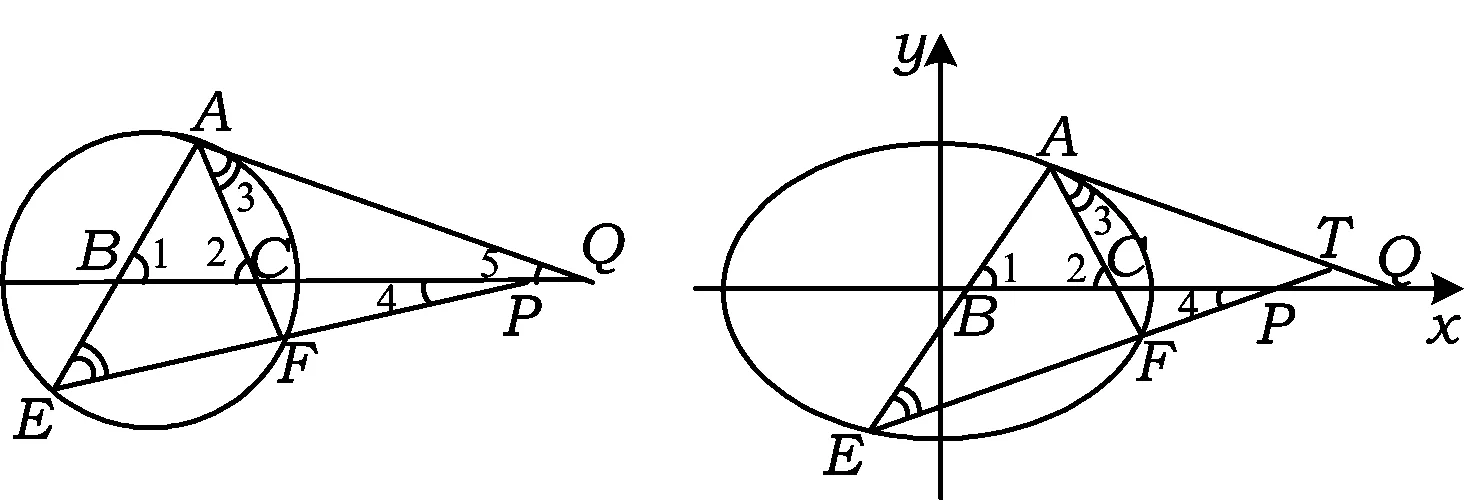
图1 图2

师：通过观察由特殊情形出发，类比猜想得到一般结论是科学研究的一种有效方法,但还要严格证明．

从而

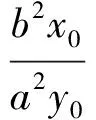
设kAE=k,则kAF=-k.又点A(x0,y0)在椭圆上,得

从而

(b2+a2k2)x2+2a2k(y0-kx0)x+

a2(y0-kx0)2-a2b2=0.

记E(x1,y1)，F(x2,y2)，则

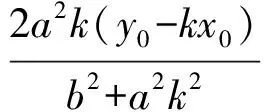
同理可得

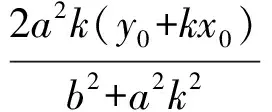
于是

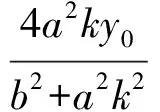
又因为y2-y0=-k(x2-x0)，y1-y0=k(x1-x0),

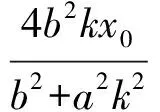
从而

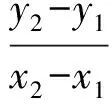
又

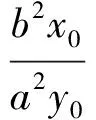
故

kEF+kAQ=0.

师：对于一个命题成立自然会想到它的逆命题是否成立呢？

证明与结论1类似．

结论1作为椭圆性质的基本定理，进而又得到以下结论：

生4：根据△TAF∽△TEA，不难得到以下结论：

片段2行到水穷处，坐看云起时

师：椭圆也有类似于圆的性质的确令人惊奇，似乎我们已经到了“水穷处”了，但同学们思考一下：椭圆除了有“切割线定理”，是否还会有“相交弦定理”呢？这样的探究就会看到“云起时”．如图2，把2条弦AE和AF移开，变成2条相交弦，切线变成割线，结论1的条件是椭圆中2条弦相交点在椭圆上，如果2条弦相交点不在椭圆上时，通过研究还可以得到一般性结论．

图3

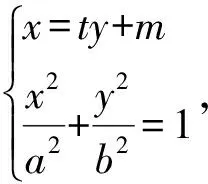
(a2+b2t2)y2+2tmb2y+b2m2-a2b2=0.

设C(x1,y1)，E(x2,y2),则

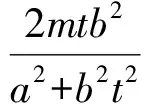
同理可设Q(x3,y3)，F(x4,y4)，则

从而

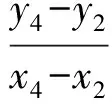
记kCD+kEF的分子为

μ= (y3-y1)[-t(y4+y2)+n-m]+

(y4-y2)[-t(y3+y1)+n-m]=-t(y3y4-

y1y2)+(n-m)[(y3+y4)-(y1+y2)]=

即kCD+kEF=0结论成立．

生5：由此,可以进一步探究△PCD∽△PEF，得出结论：

片段3会当凌绝顶,一览众山小

师：是否可以把昨天作业中的数学问题由椭圆推广到抛物线和双曲线上？

(让学生分小组讨论、探究，再由代表进行总结发言.)

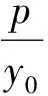
师：通过讨论分析，还可以得到更一般的结论：

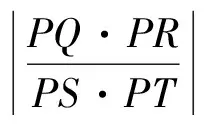
证明设圆锥曲线方程为

f(x,y)=Ax2+Bxy+Cy2+Dx+Ey+F=0,

(1)

直线PQR与直线PST的倾斜角分别为θ1,θ2，则过点P的直线PQR的参数方程为

(2)

联立式(1)，(2)，得

PQ·PR=t1·t2=

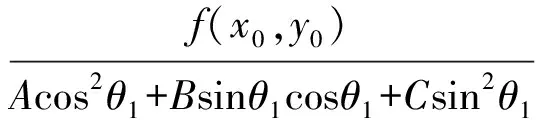
同理可得

PS·PT=t3·t4=

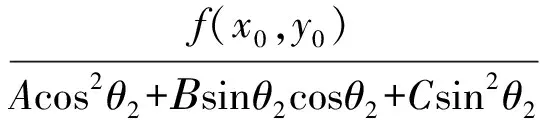
该值与点P位置无关．

特别地，当B=0,θ1+θ2=π(即直线QR与直线ST的斜率互为相反数)时，|PQ|·|PR|=|PS|·|PT|成立．

师：当圆锥曲线换成圆时，就是圆幂定理．上述证明已涵盖了圆幂定理，并且说明把圆推广到椭圆、双曲线、抛物线时，类似结论仍然成立．结论9是圆锥曲线的牛顿定理，它的特例包含了今天我们所探究的所有结论，此结论可以作为编写相关圆锥曲线试题的依据或根源．

师(结束语)：同学们，优美的结论、奇妙的数学，令人神往．在平常的学习中，要做学习的有心人，处处留心皆学问，让我们探究数学、喜欢数学、享受数学吧!

2 课后思考

2.1 摒弃知识灌输，营造探究环境

高三数学复习时间紧、任务重，教师往往把思维变成即成思路，精心备好课，准备若干解题方法，整个课堂以讲解为主，使问题解答变成可传信物，学生看到的是思维的结果，很难体会思维的过程．事实上,很多学生并不一定会像教师那样去思考、去探究，原因是：思维是靠启迪，而不是靠灌输，越是传授得一清二楚，学习者就越不会思维．因此在教学时要给学生独立思考、自由发现问题进而解决问题的机会，有意培养其自主探究的能力和习惯，从而提高学生的后期继续学习的能力．复习课营造良好的探究环境，是提高数学课堂教学效果的关键，是发展学生数学学习能力的根本．本节课教学设计的策略是启发引导学生跨越探究的三重境界，从“不畏浮云遮望眼,只缘身在最高层”的坚持到“行到水穷处，坐看云起时”的困惑再到“会当凌绝顶,一览众山小”的顶峰境界，使学生充分品味探究过程的魅力，体验数学学习的乐趣．

2.2 运用合作学习，促进有效探究

小组合作学习是新课程理念下比较常用的一种教学手段，但并不是所有的内容都适合合作学习，只有那些抽象的、深刻的、具有开放性的问题，才需要合作学习．本节课教学班级的学生属中偏下水平，如果让学生独立去思考探究，能够得到结论7和结论8的学生毕竟少数．事实证明，通过合作学习，学生的积极性得到很大的提高，课堂气氛热烈，结论7和结论8的合作发现也为师生共同探究，为得到结论9起到了很好的铺垫作用．有效的合作学习，可以使数学课堂充满活力，更能揭示数学本质，可以使数学课堂充满智慧，更有内涵，探究更有成效．

2.3 把握探究方式，提高复习效率

数学探究式课堂教学，主要是指在数学课堂教学中，学生在教师的指导下，用类似科学研究的方式去解决问题的学习方式．“类似科学研究的方式”就是让学生通过观察、比较、类比、猜想等方式发现问题，提出结论，进行推理和证明解决问题．其实质是让学生学习科学研究的思维方式，从而培养学生主动探究、体验数学发现和创造的历程，发展他们的创新意识．这节复习课从一道好题出发，从椭圆性质到一般圆锥曲线性质，从圆幂定理推测出圆锥曲线也有类似“圆幂定理”的结论，达到了“秀枝一株，嫁接成林”的目标，教学设计高屋建瓴，潜移默化，浅入深出，最后走向“以不变应万变”的“一课一例”的复习课模式．

总之，本节课通过对椭圆性质的探索，合理地运用几何直观去推测，或是出于直觉，或是通过归纳和类比，体现了一种自然思考的过程．课堂上不但提出了几个新的结论，而且在猜测和证明的过程中，体现了科学研究的一般规律，有利于激发学生的兴趣．因此，在日常教学中，我们要注意挖掘探究素材，让学生在“一题多解、一题多变、多题归一”中体会题目的数学本质，领悟解题的思想方法，促进学生创新思维的发展．

[1] 李士锜.数学学习心理[M].上海：华东师范大学出版社，2001：64-65.

[2] 王顺耿.再论圆锥曲线“相交弦定理”的探索[J].数学教学，2008(7):31-37.