少齿数非对称齿轮主动设计与温度场分析
2013-10-25田兴李威
田兴,李威
(北京科技大学机械工程学院,北京100083)
随着科技的进步,机械传动装置向小型、轻量化方向发展,少齿数齿轮传动得到了越来越多的研究和应用.为了满足用户日益严格的订制要求,齿轮的主动设计方法应运而生.Kapelevich等[1-3]运用主动设计方法对非对称齿轮的齿形做了研究,李宁等[4-6]探讨了非对称斜齿轮的啮合机理.Alipiev[7-8]在非对称齿轮的基础上,对少齿数齿轮副啮合情况做了理论分析.Anifantis等[9-11]计算了齿面摩擦热流量和对流换热系数,龚宪生等[12]对行星齿轮轮齿本体温度和闪温进行了分析.
目前,国内关于少齿数非对称渐开线齿轮的研究处于起步阶段,相关文献很少.本文运用主动设计方法研究该齿轮的啮合机理,并利用ANSYS参数化设计语言(APDL)对其温度场进行分析.
1 齿轮的主动设计
非对称齿轮主要用于单向传动,本文以工作侧齿廓为研究重点.使用传统理论方法设计齿轮时,实际啮合线要比理论啮合线短,当齿轮副齿数减少时,传动重合度很有可能小于1,所以齿轮设计的重点是尽可能延长实际啮合线.如图1,当实际啮合线与理论啮合线相等,重合度达到理论上的最大值.在这种极限情况下,啮合线开始于点N1,结束于点N2.齿顶圆ra1和齿顶圆ra2分别过啮合线的结束点N2和起始点N1.于是,非对称齿轮在传动方向上的重合度计算公式为

这就是齿轮的主动设计,通过改变齿形来提高传动质量,目的是使重合度达到潜在最大值.本文采用等变位齿轮传动,变位系数之和X1+X2=0,Xτ1+Xτ2=0.此时,非对称刀具齿条的齿形角等于非对称齿轮的压力角.

图1 基于主动设计方法的渐开线啮合Fig.1 Involute meshing based on direct design method
为了确定图1中齿轮的参数,预先选取啮合的一对齿轮的齿数z1和z2,模数m以及齿轮的潜在重合度εpd(εpd≥1),根据式(1),计算出非对称齿轮工作侧的压力角αd:
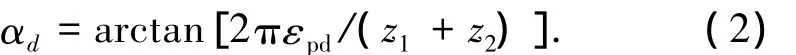
然后,根据图1的几何关系,可以得到以下参数的关系式.
1)齿顶圆压力角:

2)以节点P为界点,齿条刀具斜直线部分高度:
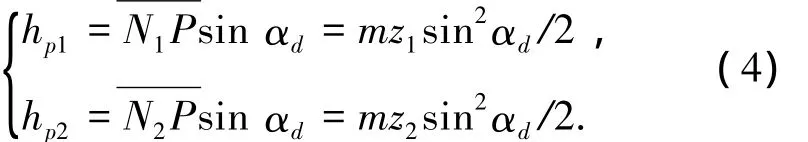
3)根据式(4),齿条刀具斜直线部分高度之和:

4)非对称齿条刀具圆角高度为
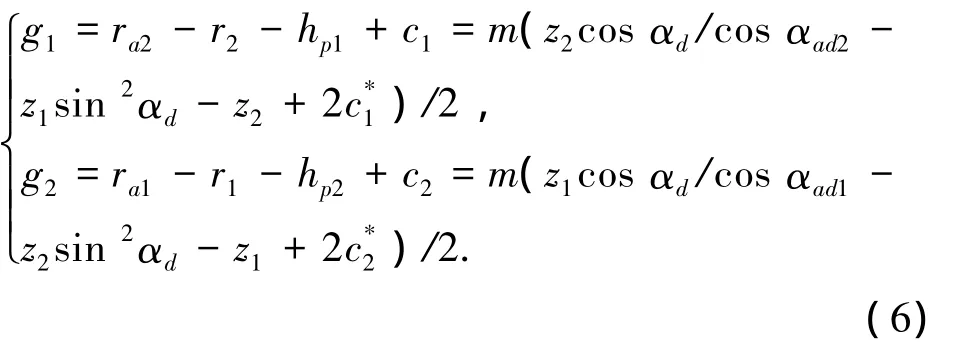
5)非对称齿条刀具齿全高:

6)非对称齿轮的径向变位系数:

7)非对称齿轮齿顶圆的齿顶厚:
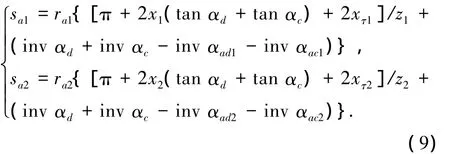
式中:inv为渐开线函数,invα=tanα-α;ra1=(0.5z1+h*a+x1)m,为齿轮1的齿顶圆半径;ra2=(0.5z2+h*a+x2)m,为齿轮2的齿顶圆半径.
8)当sa1=sa2时,切向变位均衡系数xΔτ:

运用主动设计方法,本文研究的少齿数非对称渐开线齿轮的参数如下:齿数比 z1/z2为 6/10,模数为10mm,变位系数 x1、x2分别为 0.2、-0.2,齿宽为10 cm,齿顶高系数为0.92,顶隙系数为0.18,压力角为30°/20°.
2 齿面摩擦热流量的计算
齿轮在任意啮合位置接触点C处的主动轮与从动轮的摩擦热流量可以由下式分别表示:

式中:qc1、qc2分别为主动轮和从动轮摩擦热流量;βs为摩擦热流密度分配系数;η为热量转换系数,η=0.9~0.95;f为齿面摩擦系数;σH为齿面平均接触压力;Vc为齿轮相对滑动速度;λ1、λ2分别为主动轮和从动轮导热系数;ρ1、ρ2分别为主动轮和从动轮材料密度;c1、c2分别为主动轮和从动轮材料比热容.
主动轮和从动轮选用相同的材料,所以

2.1 齿轮相对滑动速度的分析
轮齿的相对滑动是衡量摩擦热流量大小的重要因素.在分析啮合面切线方向的速度时,引入无量纲参数Γ来表示啮合线上任意点x的线性坐标.

则主动轮和从动轮沿啮合面切线方向的绝对速度V1、V2为

主动轮和从动轮沿啮合面切线方向的相对滑动速度Vc为

式中:ω为主动轮角速度,rad/s;n1、n2为主、从动轮转速,r/min;αx为主动轮任意啮合位置的压力角,rad;u为齿轮传动比.

图2 齿轮啮合示意Fig.2 Gear meshing
2.2 齿面摩擦系数的计算
影响齿面摩擦系数的因素很多,如:齿面的材料、粗糙度、润滑油动力粘度.此外,齿轮的转速和承受的载荷对齿面摩擦系数也有一定的影响.由于摩擦系数计算非常复杂,工程中通过实验测量来确定平均摩擦系数.本文根据Buckingham摩擦系数经验公式,齿面摩擦系数f可表示为

由图3综合考虑,本文取齿面摩擦系数f=0.05.
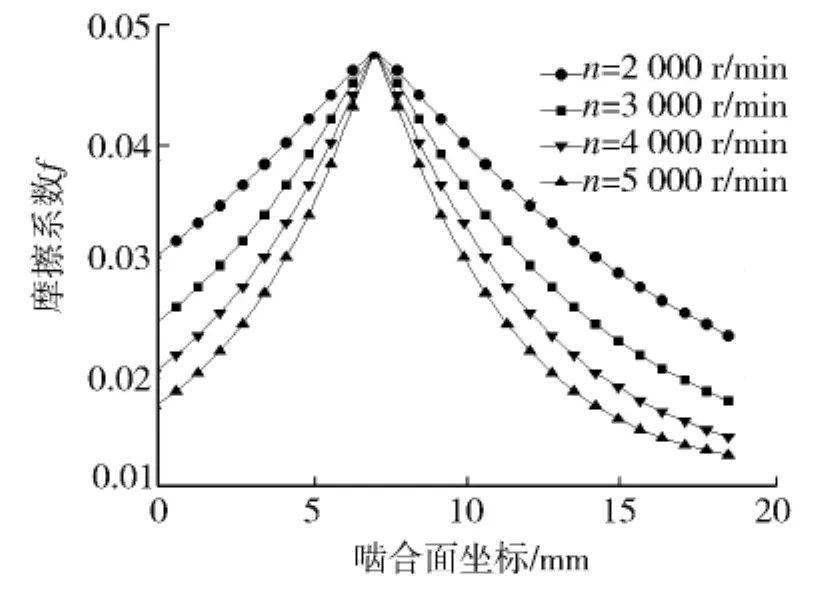
图3 齿面摩擦系数分布Fig.3 Tooth surface friction coefficient
2.3 齿面接触应力的计算
齿轮齿面平均接触压力公式为

式中:Fn为啮合齿面的法向载荷,N;vi为齿轮材料泊松比;Ei为齿轮材料弹性模量,MPa;Ri为齿轮曲率半径,mm;bH为接触线的长度,mm.
啮合点处于单齿啮合区时,其接触线长度为bH=b;当啮合点进入双齿啮合区时,接触线长度变为bH=2b.
3 对流换热系数的确定
计算齿轮润滑油的对流换热系数,本文采用的润滑油在60℃时的性能参数如下:运动粘度vf=80×10-6m2/s,比热容 cf=2 000 J/(kg·K),热导率λf=0.133 7 W/(m·K),密度 ρf=998 kg/m3.
齿轮的对流换热系数,没有成型的理论可以精确计算,下面给出的是国内外文献[9]中提供的经典公式.
端面
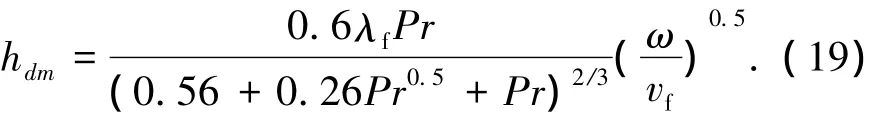
齿根、齿面

齿顶

4 轮齿本体温度场的有限元计算
4.1 轮齿温度场计算原理
轮齿温度可分为稳态本体温度和表面瞬态温度.表面瞬态温度呈周期性变化,但仅限于热表层,影响很小.所以,在进行齿轮温度场分析时,将轮齿的本体温度作为稳态温度场进行处理.
如图4,整个齿轮的求解域为D,把求解域划分为E个单元,Z个节点.在求解域D中,T=T(x,y,z)为满足边界条件的本体温度场温度函数.泛函I(T)的表达式为

式中:λg为齿轮的导热系数,T0为环境温度.
使I(T)取极小值,用δI(T)=0来计算求解域的温度函数.求解以上方程必要的边界条件如下:
工作齿面
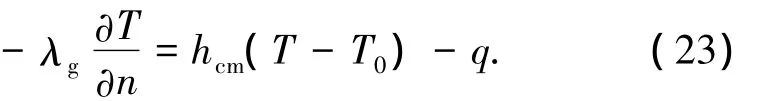
非工作齿面、齿根

齿顶

端面
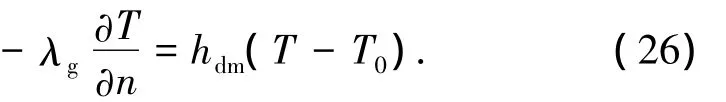
轴孔内圈

进行有限元计算时,离散计算区域,得到单元温度函数,将其代入单元的泛函Ie.于是,对I(T)变分求极值问题就转化为对I(T)各节点温度求极值问题,得到总体热平衡方程的矩阵形式,即

式中:Q为总的热流量矩阵,H为总的热传导矩阵,T为总的温度列矩阵.求解式(28),就可得到齿轮有限元模型各节点的温度值.

图4 少齿数非对称渐开线齿轮加载边界Fig.4 Loading boundary for sm all numbers of teeth
4.2 轮齿本体温度场的有限元分析
摩擦热流量是随啮合位置变化的量,在有限元分析中不能作为常数加载.本文运用APDL对摩擦热流量进行加载:用公式编制程序,计算出每一节点处的摩擦热流量,利用循环语句依次加载到单元表面上.
少齿数非对称渐开线齿轮的本体温度场分布如图5所示.由于摩擦热流量的输入,轮齿的温度明显高于齿轮轮体.齿轮的最高温度出现在分度圆靠近齿顶的位置,齿轮轮体上温度几乎相等.
从图6可以看出,沿齿轮啮合面方向,温度出现2个峰值,分别是齿根和齿顶附近;沿齿宽方向,由于轮齿端面散热条件好,轮齿表面温度沿齿宽方向对称,轮齿端面的温度值略低于中部.
图7中,当转速为3 000 r/min、载荷从183.8 N/mm增加到367.6 N/mm时,载荷比值为2,齿轮的最高温度从87.55℃增加到115.12℃,温升比为1.31.当载荷为275.7 N/mm、转速从2 000 r/min增加到4 000 r/min时,速度比值为2,齿轮的最高温度从100℃增加到109.51℃,温升比为1.10.由此可见,载荷对温度的影响比转速要大.
当齿轮的载荷和转速增时,由式(11)、(16)和(18)可知,啮合面的摩擦热流量增加.但是载荷的增加,对对流换热系数的影响很小;而转速的增加,导致对流换热系数增大.所以载荷的温升比会大于转速,载荷对温度的影响要比转速大.
从图8可以看出,齿轮最高温度和最低温度分别随着油温的增加呈线性增加.油温每增加10℃,齿轮的温度也相应增加了约10℃.油温直接影响齿轮的温度,这也说明控制油温对降低齿轮温度的重要性.
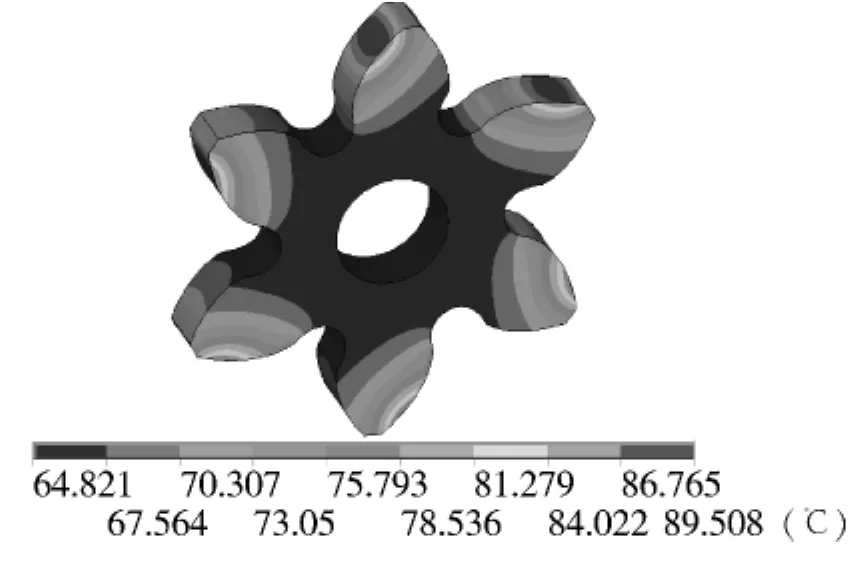
图5 本体温度场分布Fig.5 Bulk temperature field distribution

图6 啮合齿面温度分布Fig.6 Meshing surface temperature distribution

图7 齿面最高温度随载荷和转速的变化规律Fig.7 Change rule of the highest tooth surface temperature with load and speed

图8 不同油温下齿轮的温度Fig.8 Gear temperature with different oil temperatures
5 轮齿本体温度最大值近似表达式
速度、载荷和油温是影响齿轮本体温度的重要因素.为了预测在不同转速、载荷和油温下的齿轮本体最高温度,为齿轮设计提供可靠的依据,建立了少齿数非对称渐开线齿轮齿面的本体最高温度随转速、载荷和油温变化的近似表达式:

其中:

式中:k为温度系数,b为指数系数,W为法向单位线载荷,Toil为油温,Tmax为齿轮本体温度最大值.
6 少齿数非对称齿轮传动系统温度场试验
试验采用封闭功率流式齿轮试验台—MRC-1型FZG摩擦磨损试验机,试验台主要包括一对试验齿轮及一对驱动齿轮,现场试验布局如图9.

图9 齿轮试验台Fig.9 Gear experiment bench
从表1可以看出,在一定的转速和载荷范围内,有限元分析获得的仿真值以及拟合公式得到的近似值,与试验所得数据比较接近,证明了运用有限元方法分析少齿数非对称渐开线齿轮温度场的正确性.试验值比近似值要大,主要原因是有限元分析中没有加入齿轮轴,但是在试验中,齿轮轴轴承旋转摩擦生热对齿轮温度分布会产生影响.随着载荷和转速的增加,试验值与仿真值差值也逐渐加大,表明轴承摩擦生热也在增加.但是两者相差不大,也说明齿轮轴轴承摩擦生热对齿轮的温度分析影响不大.在以后的齿轮的温度仿真分析中,考虑轴承摩擦生热的影响会提高分析的精度.

表1 试验参数和结果Table 1 The experiment parameter and result
7 结论
1)运用主动设计方法,对少齿数非对称渐开线齿轮的啮合机理进行了研究,推导出了齿轮各参数的关系式.
2)在啮合面,齿根和靠近齿顶的位置,温度分别出现2个峰值,最大值出现在靠近齿顶的位置,轮齿表面温度沿齿宽方向对称,端面的温度值略低于中部.
3)转速、载荷和油温是影响齿轮温度大小和分布的重要因素,推导了少齿数齿轮齿面的本体最高温度随转速、载荷和油温变化的函数表达式,为齿轮的优化设计和润滑改进提供可靠的依据.
4)运用有限元分析获得的结果,与试验测得的数据比较接近,证明了有限元方法分析少齿数非对称渐开线齿轮温度场的正确性.温度场的分析结果,为进一步研究齿面闪温、热应力、抗胶合能力和齿轮修形提供了研究基础.
[1]KAPELEVICH A.Geometry and design of involute spur gears with asymmetric teeth[J].Mechanism and Machine Theory,2000,35(1):117-130.
[2]KAPELEVICH A.Application of gears with asymmetric teeth in turboprop engine gearbox[J].Gear Technology,2008,25(1):60-65.
[3]KAPELEVICH A,SHEKHTMAN Y.Tooth fillet pr of ile optimization for gears with symmetric and asymmetric teeth[J].Gear Technology,2009,26(7):73-79.
[4]肖望强,李威,李梅.双压力角非对称齿廓齿轮齿根弯曲应力的有限元分析[J].北京科技大学学报,2006,28(6):570.XIAO Wang qiang,LI Wei,LI Mei.Finite element analysis of the tooth root bending stress of an unsymmetric gear with double pressure angles[J].Journal of University of Science and Technology Beijing,2006,28(6):570.
[5]李宁,李威,韩建友,等.非对称齿廓渐开线斜齿圆柱齿轮的齿形设计及啮合分析[J].北京科技大学学报,2011,33(7):876-882.LINing,LIWei,HAN Jianyou,et al.Tooth pr of ile design and meshing analysis on a helical gear with asymmetric involute teeth[J].Journal of University of Science and Technology Beijing,2011,33(7):876-882.
[6]陈国定,李剑新,刘志全,等.斜齿轮非定常温度场的计算[J].西北工业大学学报,2000,18(4):11-14.CHEN Guoding,LI Jianxin,LIU Zhiquan,et al.Helical gear unsteady temperature field calculation[J].Journal of Northwestern Polytechnical University,2000,18(4):11-14.
[7]ALIPIEV O.Geometric calculation of involute spur gears defined with generalized basic rack[J].Theory of Mechanisms and Machines,2008,12(2):60-70.
[8]ALIPIEV O.Geometric design of involute spur gear drives with symmetric and asymmetric teeth using the realized potential method[J].Mechanism and Machine Theory,2011,46(1):10-32.
[9]TOWNSEND D P,AKIN L S.Analytical and experimental spur gear tooth temperature as affected by operating variables[J].Journal of Mechanical Design,1981,103(l):219-226.
[10]ANIFANTISN,DIMAROGONASA D.Flash and bulk temperatures of gear teeth due to friction[J].Journal of Mechanical Machine Theory,1993,28(1):56-61.
[11]GARDON G,ASTARITA T,CARLOMAGNO G M.Infrared heat transfer measurements on a rotating disk[J].Optical Diagnostics in Engineering,1996,1(2):1-7.
[12]龚宪生,王欢欢,张干清,等.行星齿轮轮齿本体温度场与闪温研究[J].农业机械学报,2011,42(10):209-216.GONG Xiansheng,WANG Huanhuan,ZHANG Ganqing,et al.Analysis of bulk temperature field and flash temperature for planetgear teeth[J].Transactions of the Chinese Society for Agricultural Machinery,2011,42(10):209-216.
