特殊建筑双微方法几何造型
2013-10-25张群力周平槐杨学林
张群力 周平槐 杨学林
(浙江省建筑设计研究院,杭州 310006)
建筑是凝结着人类文明历史与科学技术的智慧结晶,一个城市建筑业的发展同时标志着它的综合实力和社会精神面貌。近些年来,建筑师们不断激发灵感,大胆创新,新建筑除了往高的方向发展,同时也呈现追求造型奇特的特点,给人以强烈的视觉冲击。当代建筑设计,包括理念和方法都因为计算机技术的发展而发生着根本的变革。自由曲线曲面的造型技术已成为现代建筑几何造型的重要方法。曲线曲面的造型方法综述起来有参数样条方法、Coons曲面、Bezier曲线曲面和B样条方法,其它还有自由变形造型、偏微分方程造型、和能量法造型、小波技术造型、逆向工程造型、几何偏微分方程造型等等。当前CAD/CAM中曲面造型的主流方法为Bezier曲线曲面和 NURBS 方法[1~2]。解析曲面和自由曲面都可以用NURBS曲面(非均匀有理B样条曲面)统一表达[3~4]。
高技派大师诺曼·福斯特在再保险大厦和水晶岛项目中建筑造型采用的是一种不定向斜网格几何造型技术[5]。本文中要研究的是另一种可定向的网格(斜驶线网格)造型技术。该网格的空间螺旋结构极为优美,其倾角还可以自由选取。还是以莫斯科“水晶岛”和伦敦“瑞士再保险总部大厦”的基本曲面为例,采用微分几何与微分方程的方法建立这二个建筑的斜驶线网格几何造型。
1 斜驶线的定义及几何意义
过旋转曲面旋转轴的平面与旋转曲面的交线称为经线。斜驶线是指曲面上与经线夹角保持为定常数的曲线[6]。斜驶线又称为定向线。在航海学里称为航海线。飞机的航线也是按斜驶线划分的。在生物形态学里称为斜生线。螺线为柱面上与给定直线夹角保持为定常数的曲线,又称定倾线,是斜驶线的一种特例。在平直的欧氏空间上可用直线作为参考方向。螺线定义中借助了外围空间E3中直线的概念。但在弯曲空间(或流形)上高斯曲率不恒为0。一般不存在直线,要摆脱外围空间影响,把曲面本身作为一个空间。用曲线与径线在交点处切向量间的夹角来定义曲线与经线夹角这种内蕴定义方法更容易推广到一般流形以及高维流形上[7]。
由于斜驶线被约束在一个对称的旋转曲面上,再加上定向的几何约束,便在三维欧氏空间E3中呈现出了三维螺旋几何结构。比如,地球表面的斜驶线,由赤道出发朝着南北二极盘旋而去,无限延伸。在回转曲面上,经纬线是封闭的平面曲线,但斜驶线族却是既不封闭又互不相交的开曲线。同一倾角的斜驶线在二维流形上是互相平行的(内蕴平行)。根据曲面论基本定理,曲面是由其第一、二基本型完全确定的。曲面上由第一基本型决定的几何量与性质称为内蕴量与内蕴性质。曲面上曲线的长度、二曲线在交点处的夹角、曲线所围的曲面面积等,均是曲面的内蕴量。因此首先要求出曲面的第一基本型。曲线上的任一点邻域内曲线相对于直线的弯曲程度用曲率来衡量,曲面上任一点邻域内曲面相对于欧氏平面的弯曲程度用高斯曲率来衡量[8]。在高斯曲率恒为0的回转柱面上,斜驶线、螺线、测地线,三者微分方程是一致的[9]。
2 曲面上二曲线交点处的夹角
对于参数曲面:
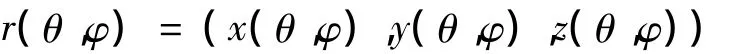
其第一基本型:
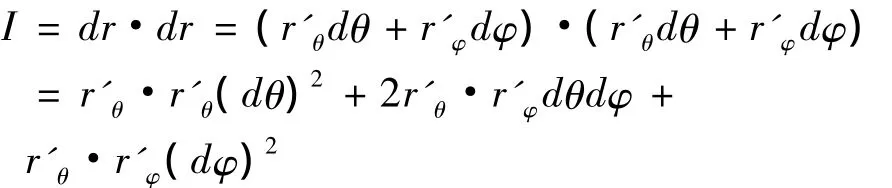
记 E=r'θ·r'θ,F=r'θ·r'φ,G=r'θ·r'φ,则有I=E(dθ)2+2Fdθdφ +G(dφ)2
其中E、F、G称为曲面S的第一基本型系数。
第二基本型:
II=n·d2r=记 L=·n,M=·n,N=·n,则有
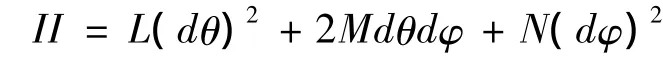
其中L、M、N称为第二基本型系数。
假设dr,δr为曲面上二曲线在交点处切向量,则有:

假定dr,δr的交角为A,根据矢量点乘的定义:

3 回转曲面斜驶线微分方程
假设θ为纬向参数,φ为经向参数,(dθ,dφ)为斜驶线切向量的方向,(δθ,δφ)为经线切向量的方向,A为经线与斜驶线的交角。根据经线定义,φ=const,故有δφ=0;由于回转曲面的经纬线正交,矢量 r'θ和r'φ垂直,即 F=r'θ·r'φ=0。由斜驶线定义得:

化简得

这是一个关于参数(内蕴变量θ,φ)的局部微分方程,其通解为(θ,φ)平面上的曲线族,特解的几何意义是平面(θ,φ)上的一条光滑曲线(θ,φ(θ)),也就是参数θ,φ间的一个几何约束关系。对该曲线作坐标映射,便可得到E3中的一条完整斜驶线线:
r(θ,φ(θ))= [x(θ,φ(θ)),y(θ,φ(θ)),z(θ,φ(θ))]从而可以在E3观察到其螺旋几何结构。正负夹角A对应左右倾两条斜驶线,这二条空间曲线镜象对称。
3.1 球面上的斜驶线
球面是半圆弧回转面,其参数方程为:
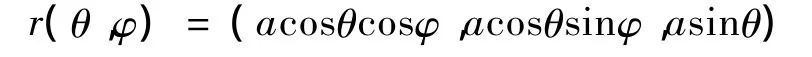
分别求导:
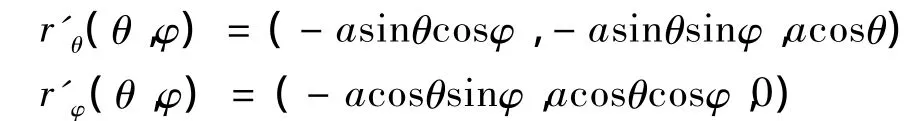
因此有:
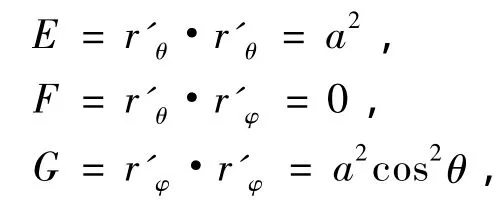
球面的第一、二基本形式:

对应高斯曲率K=LN/EG=1/a2,为正的定常数。
由式(1)可得,球面上的斜驶线约束微分方程为:

该方程的通解为:

式中c为任意实常数。
将解回代到球面参数方程,可得球面上的一条斜驶线:
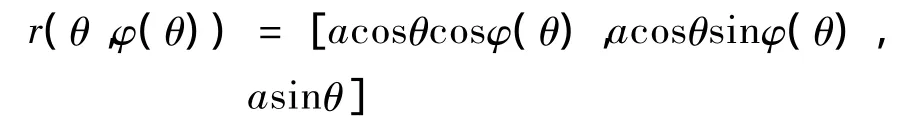
图1为上述方程对应的斜驶线。可以看出,斜驶线在球面上无限盘旋,向两极延伸,但与两个极点永不重合。

图1 球面上的斜驶线
3.2 圆柱面上的斜驶线
圆柱面参数方程为:
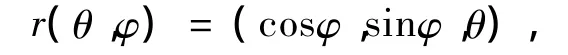
求导得
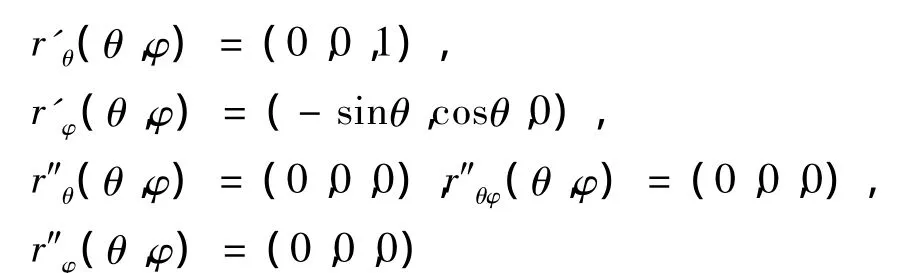
由此可得单位法向量

高斯曲率K=LN/EG=0。
由式(1)可得,圆柱面上的斜驶线约束微分方程为:
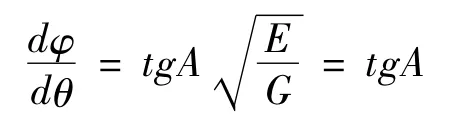
即

该方程的通解为

令tgA=1,并假设初始条件为:φ =0,θ=0,则得c=0,对应特解为

经坐标映射得斜驶线方程:
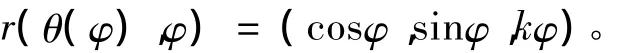
这正是圆柱螺线方程。
4 伪球面上的斜驶线——莫斯科“水晶岛”
莫斯科斥巨资正在兴建的全球最大型建筑物——“水晶岛”,图2为其效果图。水晶岛以“楼中城”的概念为主,高约457m,可容纳3万人,建筑面积250万m2。建成后将成为全世界单体面积最大的建筑物。

图2 水晶岛效果图
通过伪球面上的斜驶线,可以得到水晶岛的建筑造型。伪球面是负常高斯曲率曲面,由曳物线绕其渐近线z轴旋转而形成的回转曲面。曳物线,亦称追迹曲线,是指被曳拉物体受垂直于初始静止状态时绳线方向的牵引力作用下的运动轨迹[10],其参数方程为:
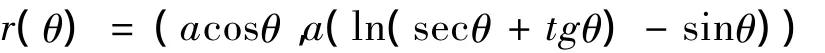
绕z轴旋转得伪球面参数方程:
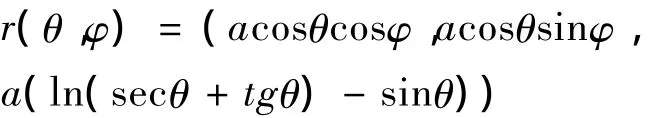
偏导得:
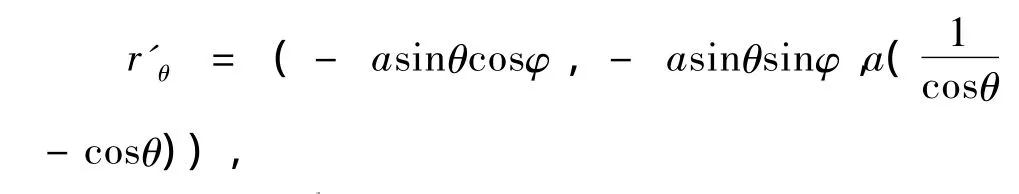

图3 曳物线参数示意图
r'φ=(- a cosθcosφ,a cosθsinφ,0),因此,第一基本型系数:
E=a2tg2θ,F=0,G=a2cos2θ,第一基本形式:
Ι=a2tg2θdθ2+a2cos2θdφ2,单位法向量计算并化简后得

伪球面的等距面方程为:

其中λ0为给定常数。每一条斜驶线在等距面上有一条对应的曲线,二者互为E3空间中的外在等距线。
令 ω =a ln(cosθ),则有

因此,第一基本型可化简为

高斯曲率:
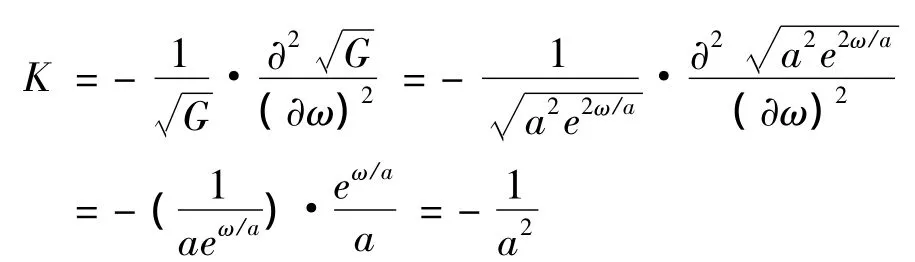
为负的定常数。
由式(1)可得,伪球面上的斜驶线约束微分方程为:

即

其通解为

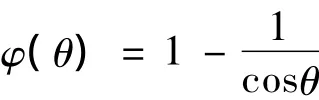
回代到伪球面的参数方程,得伪球面上的一条斜驶线:

假定式(3)中的参数a=10000;将连续参数θ进行离散,当θ越接近 π/2,φ(θ)值增长越快。因此为保证整体效果,当θ<70°时每隔5°取一个数据点;当70°≤θ <80°时间隔为 1°;当 80°≤θ <85°时间隔为0.1°;当 85°≤θ <88°时间隔为 0.01 弧度;当88°≤θ<89°时间隔为0.001弧度。表1为各区段典型节点的坐标。用样条曲线连接相邻数据点得到一条伪球面上斜驶线的样条逼近曲线,将此样条曲线线环向阵列,即以z轴为旋转轴,旋转复制24次,得到24条斜驶线。再将24条斜驶线以x0z平面作镜像复制,便得到一个空间对称的几何图形。该图形的对称性可由一个24阶旋转变换群来表征。这就是水晶岛的斜驶线网格造型,如图4所示。

表1 伪球面上的斜驶线典型离散点坐标
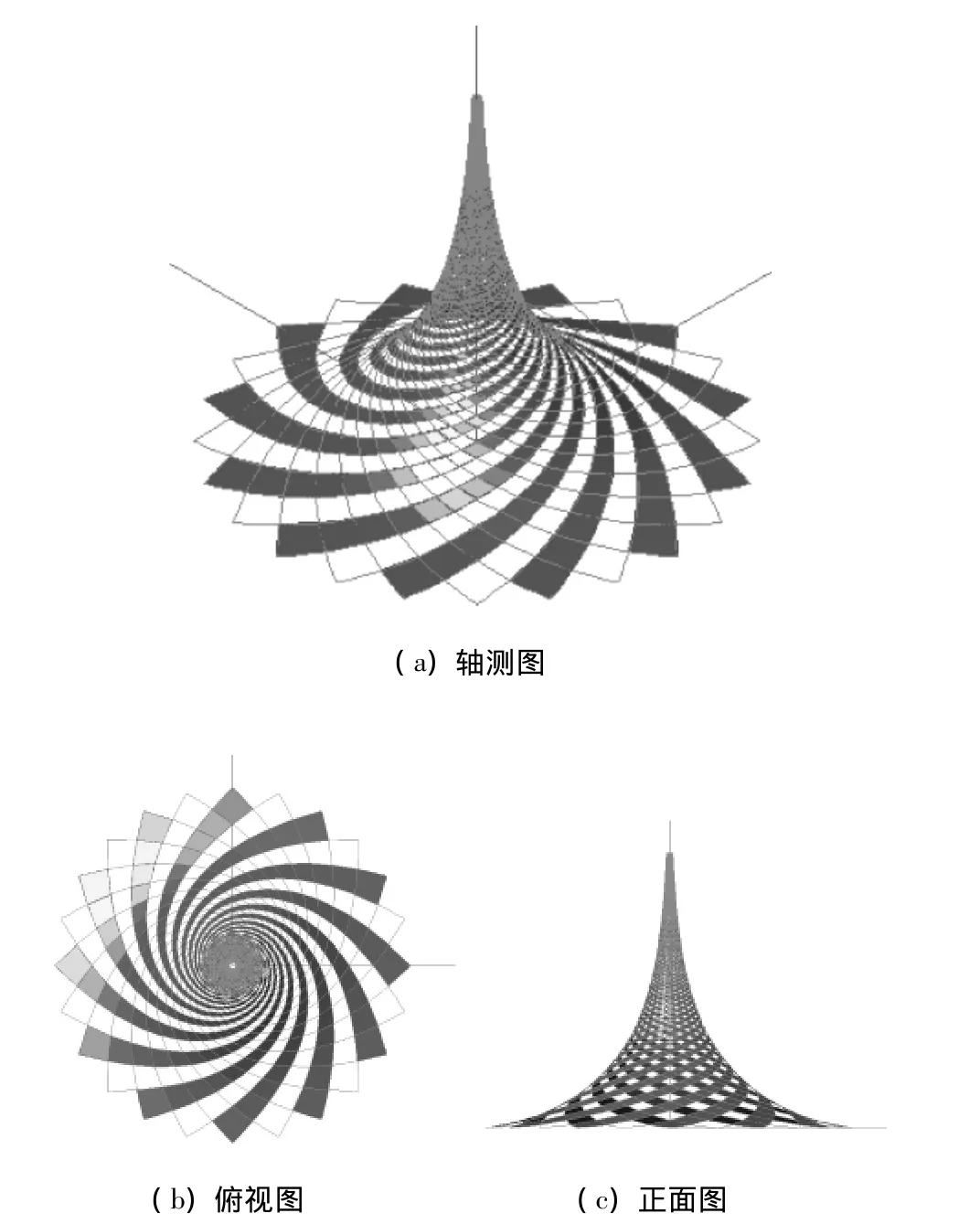
图4 水晶岛几何模型
5 劣圆弧回转面上的斜驶线——伦敦“瑞士再保险总部大厦”
瑞士再保险大厦是伦敦第一座高层生态建筑,已成为了欧洲金融中心办公建筑的里程碑式建筑。大厦的设计表达了高度激进的高层生态建筑意识,借助空气动力学的研究,大厦取得了最大程度的自然采光和通风,并将建筑运转的能耗降至最低。大厦高180m,40层,打破了传统办公建筑设计的“火柴盒”式结构,圆弧形的设计使底部和顶部渐渐收紧形成曲面,将大厦的轮廓线最大程度地融入周围建筑和街道环境之中,并使底层广场能够得到最多的日照。图5为建成后的实景图。
通过劣圆弧回转面上的斜驶线,可以得到大厦的建筑造型。劣圆弧在x0z平面上的母线方程,各参数的具体含义如图6所示:


图5 瑞士再保险大厦实景图

图6 劣圆弧参数示意图
劣圆弧回转面参数方程:
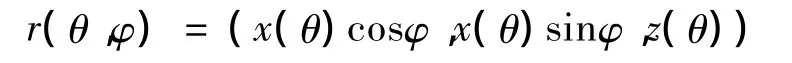

求导得

其中 v(θ)=au(θ)- d
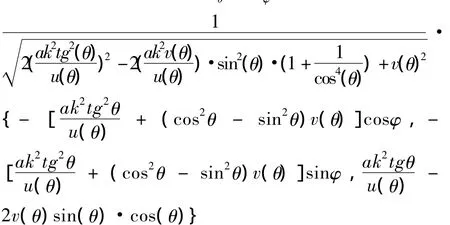
劣圆弧回转面的等距面方程为:
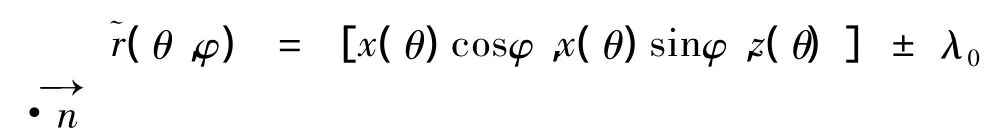
回转曲面上经纬线是曲率线,因此劣圆弧回转面上任一点经线的曲率为k1=1/a,纬线的曲率为k2,相应高斯曲率为[11]:

第一基本型系数:
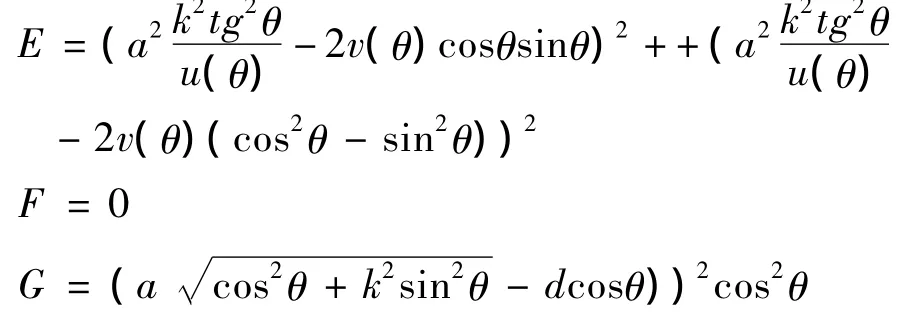
从式(1)可得劣圆弧回转面上的斜驶线约束微分方程为:

两边积分,得

从而将斜驶线约束微分方程的求解,转化为求不定积分。经Matlab验算,式(4)无法求得用基本函数表达的解析解。改用数值积分方法,所谓求数值积分,就是计算原函数F(x)(不论能否积出)在一系列离散点x0<x1<x2<…xn<…的近似值。利用Matlab的常用数值积分函数Quad函数来实现,Quad函数是采用自适应步长的辛普森求积法[12]。
r(θi,φ(θi))=(x(θi)cosφ(θi),x(θi)sinφ(θi),z(θi))于是得到E3中斜驶线上对应的一组离散点坐标(xi,yi,zi),i=1,2,…n。
假定斜驶线与经线的夹角A=30°,a=140×5/3=233.333,d=4/5a=186.666。k2=(a2- d2)/a2=0.36,由 matlab 数值积分得到 θi与 φ(θi)的关系,便可求得各点坐标如表2。然后利用与水晶岛类似的方法,得到再保险大厦的斜驶线网格造型,如图7所示。由图可知劣圆弧旋转面的顶部较为尖锐。而由相关介绍资料,再保险大厦顶部设计是将劣圆弧渐渐收紧形成曲面。因此需要采取“压顶技术”,也就是顶部保持x、y坐标不变的情况下,将z坐标乘以一个介于0和1之间的渐变的权系数。
同样采用样条曲线逼近,环向列阵、镜像复制等几何操作就得到再保险大厦的斜驶线网格造型。
6 小结
莫斯科“水晶岛”的基本造型曲面是一个沿高度方向进行压缩的伪球面,伦敦“瑞士再保险总部大厦”的基本造型曲面是一个接近于劣圆弧回转面的自由曲面。利用微分几何、微分方程方法,推导出伪球面和劣圆弧回转面上的斜驶线微分方程。伪球面上斜驶线微分方程可求得解析解,劣圆弧回转面上的斜驶线只能获得数值解。每种曲面上只需求出一条斜驶线上的若干个离散点坐标,用样条曲线依次连接,得到斜驶线的样条逼近。将样条曲线进行环形阵列和镜像,分别得到莫斯科“水晶岛”和伦敦“瑞士再保险总部大厦”的斜驶线网格建筑造型。由基本曲面上的法向量再求出其等距面方程,便可进行幕墙与结构构件的布置。
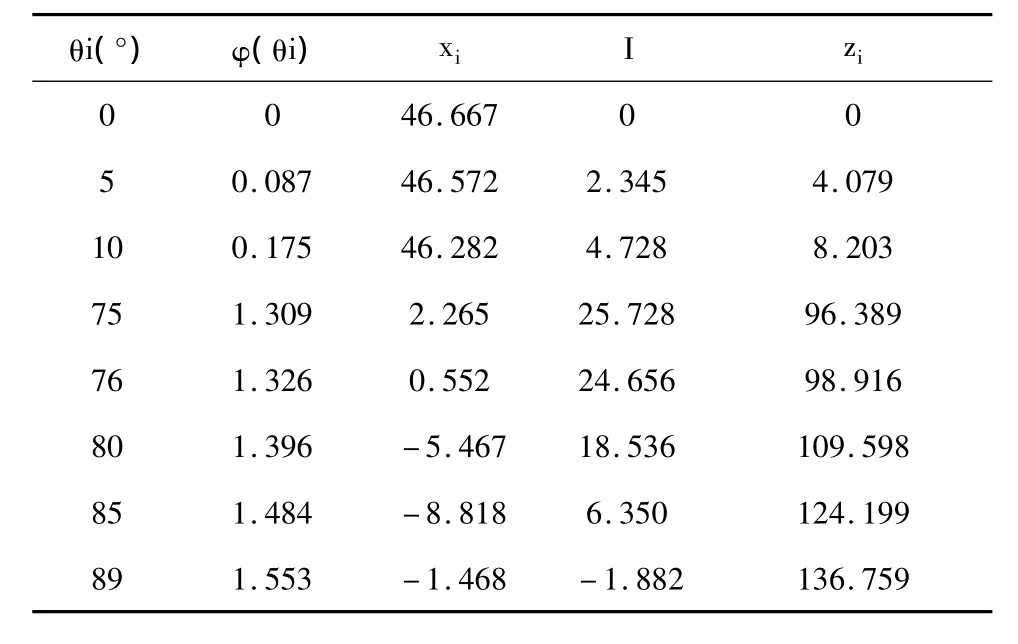
表2 劣圆弧回转面上的斜驶线典型离散点坐标

图7 瑞士再保险大厦几何模型
[1]丁汉,朱利民.复杂曲面数字化制造的几何学理论和方法[M].北京:科学出版社,2011.
[2]徐国良.计算几何中的几何偏微分方程方法[M].北京:科学出版社,2008.
[3]朱心雄.自由曲线曲面造型技术[M].北京:科学出版社,2008.
[4]曾旭东,王大川,陈辉.参数化建模[M].湖北:华中科技大学出版社,2011.
[5]张群力,周平槐等.基于软件Rhino的异型建筑几何造型方法[J].浙江建筑,Vol.(30),2013.
[6]陈维恒.微分几何[M].北京:北京大学出版社,2006.
[7]陈维恒.微分流形初步[M].北京:高等教育出版社,1998.
[8]陈维恒,李兴校.黎曼几何引论[M].北京:北京大学出版社,2002.
[9]田宗若,田宗漱.复合材料簿壳最佳缠绕状态的研究[J].机械科学与技术,Vol.20(3),2001.
[10]数学词典[M].上海:上海辞书出版社,1992.
[11]彭家贵,陈卿.微分几何[M].北京:高等教育出版社,2006.
[12]张德丰.Matlab数值分析与应用[M].北京:国防工业出版社,2007.
