2个渐近拟伪压缩型非自映像公共不动点的强收敛性定理*

石惠敏, 王元恒

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

2个渐近拟伪压缩型非自映像公共不动点的强收敛性定理*

石惠敏, 王元恒

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

在实Banach空间中引入了一种关于2个渐近拟伪压缩型非自映像的新型带误差修正的混合Ishikawa迭代序列;并在适当的条件下,巧妙证明了此迭代序列的强收敛性.所得结果改进和推广了许多已有结果.

渐近拟伪压缩;非自映像;带误差修正的Ishikawa 迭代;公共不动点

0 引 言

在非线性分析中,不动点问题是人们比较关注的重点问题之一,因为这类问题在微分方程、优化理论、通讯工程、图像处理和理论物理等方面都有着广泛的应用.近年来,人们分别从空间、 映像以及映像满足的条件等方面对不动点的问题做了进一步的研究,并得到了许多结果[1-7].2003年,Chidume等[8]在一致凸Banach空间中首先提出了渐近非扩张非自映像的概念.之后,许多学者研究了渐近非扩张非自映像、渐近伪压缩自或非自映像不动点的强收敛性问题.2008年,文献[9]引入渐近拟伪压缩型映像,并得到以下结果:

定理1[9]设X是任意实Banch空间,K是X的非空凸集,T:K→K是一致L-Lipschitz的渐近拟伪压缩型映像,其渐近系数为kn≥1.假设αn,βn,γn,δn是[0,1]中的实序列,且满足以下条件:

1)αn+γn≤1,βn+δn≤1;

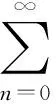
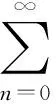
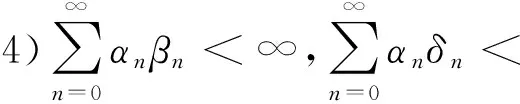
给定x0∈K,{xn}是带误差的修改的Ishikawa迭代序列.任给x*∈F(T),则{xn}强收敛于x*的充要条件是存在一严格增加函数φ:[0,∞)→[0,∞),φ(0)=0,使得

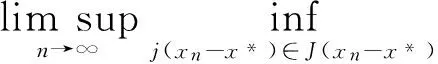
受以上文献的启发,本文在任意实Banach空间中,对于2个渐近拟伪压缩型非自映像的公共不动点,引入一种新型带误差修正的Ishikawa迭代序列,并在适当的条件下,巧妙利用该迭代格式的特征证明了它的强收敛性.

因为本文所研究的是2个映像T1和T2的公共不动点,研究的映像是非自映像(包括自映像),其迭代格式是2个映像混合的修正的新Ishikawa迭代格式,所以本文结果在一定程度上改进和推广了文献[1-6,8-9]的结果.

1 预备知识

设X是一个实Banach空间,其对偶空间为X*,〈5,5〉表示X与X*之间的广义配对.J:X→2X*是由下列定义的正规对偶映像:

J(x)={f∈X*:〈x,f〉=‖x‖‖f‖,‖x‖=‖f‖},∀x∈X.

设K是实Banach空间X的非空子集.若存在从X到K上的连续映像P,使得Px=x,∀x∈K,则称K为是X的收缩核,称P为X到K上的收缩映像.

定义1设K是实Banach空间X的收缩核,具有收缩映像P:X→K,T是从K到X的映像.

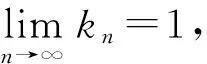
〈T(PT)n-1x-T(PT)n-1y,j(x-y)〉≤kn‖x-y‖2,

则称T为广义渐近伪压缩的非自映像.

2)若对∀x,y∈K,存在L≥1,使得

‖T(PT)n-1x-T(PT)n-1y‖≤L‖x-y‖,

则称T为广义一致L-lipschitz的非自映像.

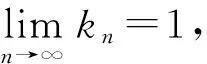
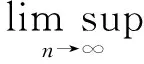
则称T为广义渐近伪压缩型非自映像.

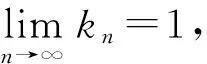
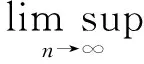
则称T为广义渐近拟伪压缩型非自映像.

注1由定义1知,广义渐近伪压缩非自映像和广义渐近伪压缩型非自映像都是广义渐近拟伪压缩型非自映像的推广.

定义2设X是实Banach空间,K是X的收缩核,具有收缩映像P:X→K,映像T1,T2都是广义一致L-Lipschitz的非自映像,且T1是广义渐近拟伪压缩型非自映像.

称由下式定义的序列{xn}为新型带误差修正的混合Ishikawa迭代序列:

式(1)中:{αn},{βn},{γn},{α′n},{β′n},{γ′n}都是[0,1]中的数列;{μn},{υn}有界.

引理1[9]设φ(s)是实的[0,+∞]上的严格增加函数,且φ(0)=0,n0是一个非负整数.若当n≥n0时,An,Bn,Cn,εn和αn都是非负整数并且满足如下条件:

1)An+1≤(1+Bn)An-αnφ(An+1)+αnεn+Cn;

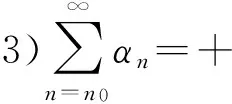
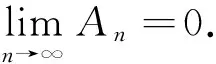
2 主要结果

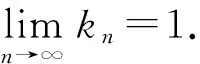
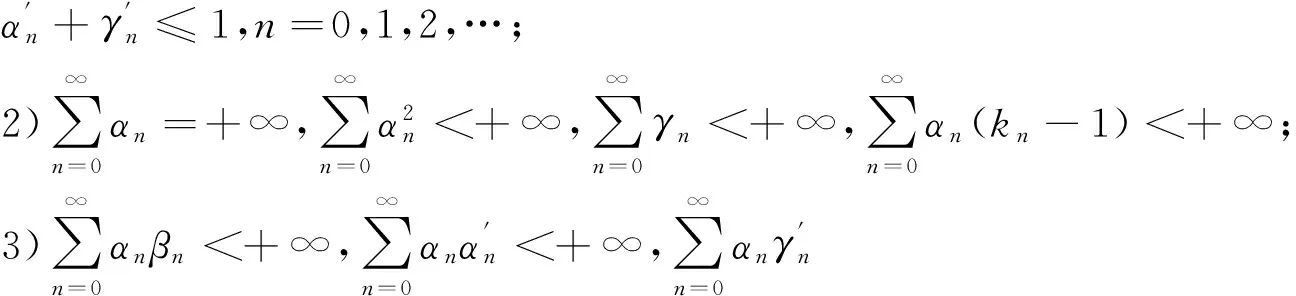
给定x1∈K,{xn}由迭代序列(1)生成.对于x*∈F, 有如下结果:

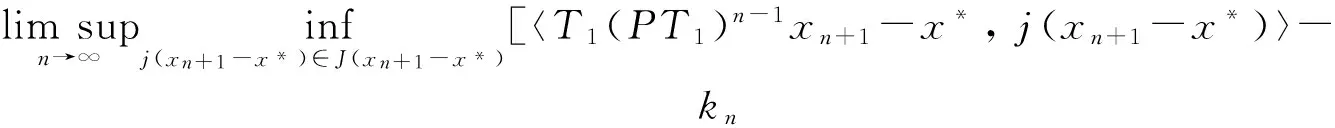
(3)

则{xn}强收敛于x*.

②反之,若{xn}强收敛于x*,则存在非负增函数φ:[0,∞)→[0,∞),且φ(0)=0,使得式(3)成立.

证明 ①设ε′n=inf[〈T1(PT1)n-1xn+1-x*,j(xn+1-x*)〉-kn‖xn+1-x*‖2+φ(‖xn+1-x*‖)],εn=max{ε′n,0}+1/n,则存在j(xn+1-x*)∈J(xn+1-x*),使得

〈T1(PT1)n-1xn+1-x*,j(xn+1-x*)〉-kn‖xn+1-x*‖2+φ(‖xn+1-x*‖)<ε′n+1/n≤εn.

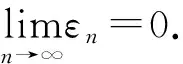
‖δn-x*‖≤β′n‖T2(PT2)xn-x*‖+(1-β′n)‖xn-x*‖≤β′nL‖xn-x*‖+‖xn-x*‖;

‖yn-x*‖≤(1-α′n-γ′n)‖xn-x*‖+α′nL‖δn-x*‖+γ′n‖υn-x*‖≤

‖xn-x*‖+α′nβ′nL2‖xn-x*‖+α′nL‖xn-x*‖+γ′nM=

(1+α′nβ′nL2+α′nL)‖xn-x*‖+γ′nM≤(1+L+L2)‖xn-x*‖+M;

‖σn-x*‖≤βn‖T1(PT1)n-1yn-x*‖+(1-βn)‖yn-x*‖≤

βnL‖yn-x*‖+‖yn-x*‖≤(1+L)(1+L+L2)‖xn-x*‖+(1+L)M;

‖yn-xn+1‖≤αnL‖σn-x*‖+αn‖xn-x*‖+α′nL‖δn-x*‖+

α′n‖xn-x*‖+(γn+γ′n)‖xn-x*‖+(γn+γ′n)M≤

αnL[(1+L)(1+L+L2)‖xn-x*‖+(1+L)M]+

α′nL[(1+β′nL)‖xn-x*‖]+(αn+α′n+γn+γ′n)‖xn-x*‖+(γn+γ′n)M≤

[αnL(1+L)(1+L+L2)+α′nL(1+β′nL)+αn+α′n+γn+γ′n]‖xn-x*‖+

(αnL(1+L)+γn+γ′n)M;

‖σn-xn+1‖≤‖yn-xn+1‖+βn‖T1(PT1)n-1yn-yn‖≤sn‖xn-x*‖+tn.

其中:

sn=αnL(1+L)(1+L+L2)+α′nL(1+β′nL)+αn+α′n+γn+γ′n+βn(1+L)(1+L+L2);

tn=[αnL(1+L)+γn+γ′n+βn(1+L)]M.

于是:

2αn〈T1(PT1)n-1σn-T1(PT1)n-1xn+1,j(xn+1-x*)〉≤

2αnL‖xn+1-x*‖‖σn-xn+1‖≤2αnL‖xn+1-x*‖[sn‖xn-x*‖+tn];

(4)

‖xn+1-x*‖2≤(1-αn-γn)2‖xn-x*‖2+

2αn〈T1(PT1)n-1σn-x*,j(xn+1-x*)〉+2γn〈μn-x*,j(xn+1-x*〉≤

(1-αn-γn)2‖xn-x*‖2+2αn〈T1(PT1)n-1σn-T1(PT1)n-1xn+1,j(xn+1-x*)〉+

2αn〈T1(PT1)n-1xn+1-x*,j(xn+1-x*)〉+2γnM‖xn+1-x*‖.

(5)

对于式(5)右边第3项,有

2αn〈T1(PT1)n-1xn+1-x*,j(xn+1-x*)〉=2αndn+2αn[kn‖xn+1-x*‖2-φ(‖xn+1-x*‖)]≤

2αnεn+2αn[kn‖xn+1-x*‖2-φ(‖xn+1-x*‖)].

其中,

dn=〈T1(PT1)n-1xn+1-x*,j(xn+1-x*)〉-kn‖xn+1-x*‖2+φ(‖xn+1-x*‖)≤εn.

把式(4)代入式(5)并化简得

‖xn+1-x*‖2≤(1-αn)2‖xn-x*‖2+2αnεn+2αnkn‖xn+1-x*‖2-2αnφ(‖xn+1-x*‖)+

2αnL(sn‖xn-x*‖+tn)‖xn+1-x*‖+2γnM‖xn+1-x*‖.

(6)

引入下列记号:

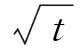
ξn=Lαnsn=L2α2n(1+L)(1+L+L2)+αnα′nL2(1+β′nL)+α2nL+

αnα′nL+Lαnγn+Lαnγ′n+Lαnβn(1+L)(1+L+L2);

(7)

ρn=Lαntn+Mγn=[α2nL2(1+L)+Lαnγn+Lαnγ′n+αnβn(L+L2)]M+γnM.

(8)

则式(6)化简为

An+1≤(1-αn)2An+2αnεn+2αnknAn+1-αnφ(An+1)+2(ξn‖xn-x*‖+ρn)‖xn+1-x*‖.

利用不等式2ab≤a2+b2得

An+1≤(1-αn)2An+2αnεn+2αnknAn+1-αnφ(An+1)+ξn(An+An+1)+ρn(1+An+1)=

(1-2αn+α2n+ξn)An+(2αnkn+ξn+ρn)An+1-αnφ(An+1)+2αnεn+ρn.

(9)

根据假设条件,由式(7)和式(8)得

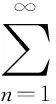
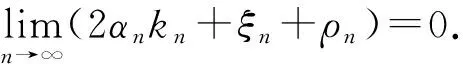
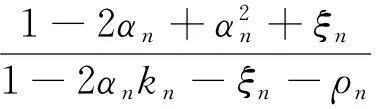
当n≥n0时,0≤Bn≤2[2αn(kn-1)+α2n+2ξn+ρn],0≤Cn≤2ρn,由式(9)得

An+1≤(1+Bn)An-αnφ(An+1)+4αnεn+Cn,∀n≥n0.

‖xn-x*‖2=0.

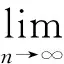
②设{xn}强收敛于x*∈F,由于xn∈K,且T:K→X是广义渐近拟伪压缩型非自映像,根据广义渐近拟伪压缩型非自映像的定义,有

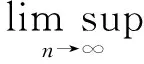
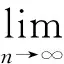
注2由于具有不动点的广义渐近伪压缩型非自映像是广义渐近拟伪压缩型非自映像的特例,所以对于渐近伪压缩型非自映像也有相应结论成立.

注3显然,定理2中,若非自映像T1,T2:K→K是自映像,则可以在迭代式(1)中取非扩张收缩映像P=I为恒等映像,式(1)即为自映像的新型带误差修正的混合Ishikawa迭代序列;若再对于2个映像有T1=T2=T,则式(1)即为自映像的新型带误差修正的Ishikawa迭代序列;若再进一步有βn=β′n=0,则式(1)即为通常的自映像的带误差的Ishikawa迭代序列.特别当T1=T2=T:K→K是自映像,P=I为恒等映像,βn=β′n=0时,定理 2 就是文献[9]中的定理 3.1(即本文的定理1).因此,本文的结果在一定程度上推广和改进了许多已有的结果,例如文献[1-6,8-9]的结果.

[1]Chang S S.Some results for asymptotically pseudo-contractive mappings and asymptotically nonexpansive mappings[J].Proc Amer Math Soc,2001,129(3):845-853.

[2]潘灵荣,王元恒.伪压缩映像修正迭代序列的强收敛性[J].浙江师范大学学报:自然科学版,2008,31(4):397-400.

[3]曾六川.Banach空间中带误差的修改的Ishikawa迭代程序[J].数学学报,2004,47(2):219-228.

[4]王绍荣,王彭德,杨泽恒,等.一致L-Lipschitz的渐近伪压缩映像不动点的Ishikawa迭代逼近问题[J].系统科学与数学,2010,30(9):1206-1212.

[5]王元恒,徐卫.非扩张映像不动点的一种变形迭代算法[J].浙江大学学报:理学版,2009,36(3):259-263.

[6]曾六川.关于渐近伪压缩型映像的不动点的迭代构造[J].系统科学与数学,2004,24(2):261-270.

[7]罗红平,王元恒.三重复合修正的Ishikawa迭代序列的强收敛性[J].浙江师范大学学报:自然科学版,2013,36(1):31-36.

[8]Chidume C E,Ofoedu E U,Zegeye H.Strong and weak convergence theorems for asymptotically nonexpansive mappings[J].J Math Anal Appl,2003,280:364-374.

[9]向长合.一致L-Lipschitz的渐近拟伪压缩型映像迭代收敛的充要条件[J].系统科学与数学,2008,28(4):447-455.

[10]王元恒,曾六川.Banach空间中广义投影变形迭代法的收敛性[J].数学年刊:A,2009,30(1):55-62.

(责任编辑 陶立方)

Strongconvergencetheoremsforcommonfixedpointsoftwoasymptoticallyquasipseudo-contractivetypenonself-mappings

SHI Huimin, WANG Yuanheng

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

It was introduced a new modified hybrid Ishikawa iterative sequence with error for common fixed points of two asymptotically quasi pseudo-contractive type nonself-mappings in a real Banach space. By manipulating the iterative format, some strong convergence theorems were proved under suitable assumptions. The results improved and generalized the existed results in literatures.

asymptotically quasi pseudo-contractive type; nonself-mapping; modified Ishikawa iteration with error; common fixed point

O177.91

A

1001-5051(2013)04-0396-05

2013-09-03

国家自然科学基金资助项目(11271330);浙江省自然科学基金资助项目(Y6110270)

石惠敏(1987-),女,河南焦作人,硕士研究生.研究方向：非线性泛函分析.

王元恒.Email: yhwang@zjnu.cn