若干介观体系的散射矩阵对称性质的一些讨论*

蒋永进， 徐 勇

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

若干介观体系的散射矩阵对称性质的一些讨论*

蒋永进， 徐 勇

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

散射矩阵是刻画许多满足量子相干性介观体系的电子输运性质的重要理论工具.结合几个介观体系的量子力学散射问题，讨论了体系的对称性对散射矩阵对称性的重要影响.几个被讨论的例子包括：1)满足时间反演不变性的自旋轨道耦合体系；2)含单轴应变的石墨烯(满足中心反演对称)体系；3)含有Majorana费米子(手征Majorana粒子的一维波导模式或Majorana束缚态)的2个典型问题.从系统的对称性推导散射矩阵的对称性，进而对体系的输运性质得出一些定性的理解.在某些场合，依据散射矩阵的对称性甚至可以对体系的电子结构的拓扑性质给出预言.

散射矩阵；对称性；自旋轨道耦合；石墨烯；Majorana费米子

0 引 言

介于宏观(μm尺度及以上)和微观(原子尺度)之间的物理体系往往称为介观体系[1-3].一般地说，当一个实际的三维体系的3个尺度至少1个是介观尺度的时候，即可以称之为介观体系.介观体系的主要特点之一是电子在穿越体系时可以维持量子相干性.著名的Landauer-Buttiker理论[2]就是描述电子在介观体系中的输运过程的主要理论框架.在此理论中，导线被描述成无多体相互作用的半无限长的一维体系，在无限远处与给定化学势的电极相连.由无穷远处的电极沿着导线入射的电子被介观体系散射，经由各导线至无穷远处的各个电极，整个过程被描述成标准的量子力学散射问题.输运过程的不可逆性完全在于各电极中的热平衡效应抹杀了入射到该电极的动量、相位和能量的信息[3].

对介观体系的散射矩阵加以研究，是理解体系输运性质的中心问题.在很多研究工作中，人们往往把电导和各种非平衡物理量的计算用非平衡Green函数等理论工具来表达[2,4]，这样可以帮助我们对较大的体系进行有效的叠代运算，甚至考虑体系的电子相互作用，而其缺点是可能掩盖掉体系的某些对称信息.在很多问题中，根据系统的对称性直接导出散射矩阵的对称性质是很有帮助的[5-6]. 近年来，在对一些新材料，如石墨烯[7]、拓扑绝缘体的边缘态[8-9]、含Majorana粒子的输运性质的研究中[10-11]，人们考虑的体系往往可以约化为一维散射问题.很多时候，这些问题中的散射矩阵本身可以严格求解出来，而对称性的分析可以帮助我们更深地理解蕴含的物理内容.最近的一些理论进展表明[12-13]，散射矩阵(往往是其反射子矩阵)的形式，甚至可以用来对体系的拓扑性质进行一一的刻画.

本文将结合笔者近些年的一些研究工作，以及文献上的一些热点问题，给出几个体系的散射矩阵的对称性分析，由此显示，对散射矩阵的形式的研究，的确是我们认识各种介观系统的一条重要途径.

1 满足时间反演不变性的自旋轨道耦合体系

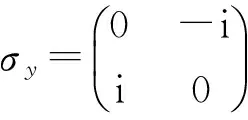
1.1无自旋轨道耦合的普通导线[14]

考虑1个一维二端系统.中间散射区域含有自旋轨道耦合相互作用，两边是理想的导线.在给定状态的能量E下，在左右导线上，粒子的状态可以一般地写成本征态|dσ>的线性组合.其中，量子数d描述本征态(在坐标表象中为平面波形式)的速度方向，d=1表示右行波，而d=-1表示左行波；σ代表本征态的自旋量子数，在给定自旋z方向表象下，可取σ=1(记为↑)和σ=-1(记为↓).显然，这些线性组合的系数就构成(dσ)表象下的波函数.在左右导线上，可分别将状态波函数写成如下形式:

式(1)～式(2)中:上标in或者out是散射过程的入射波和出射波;L和R则代表左右两边.笔者用a=(φinL↑,φinL↓,φinR↑,φinR↓)T作为入射波矢量，而用b=(φoutL↑,φoutL↓,φoutR↑,φoutR↓)T来构成散射波矢量.根据散射矩阵的定义，散射矩阵S满足

从而，

以上我们利用了S的幺正性.由式(3)，有

式(5)中：Θb=(-iσy)b*；Θa=(-iσy)a*.由于时间反演对称性，ΘSΘ-1=S-1(注意Θ使入射波和出射波地位互换).从而

结合式(4)可得，

这就是Θ不变性对散射矩阵给出的对称约束.为明确起见，以上笔者讨论了只有左右2根导线的问题.其实对于存在任意根导线的体系(以及每根导线存在多个通道的情形)，照样可以得到式(7).根据这个对称性，可推得散射矩阵的一般形式[16]

式(8)中：Sαβ为散射矩阵在第α根导线和第β根导线之间的矩阵元；Uαβ为行列式等于1的二维方阵.对于体系只有2根单模导线的情形，可进一步证明Uαβ为SU(2)矩阵；rα,rβ和tαβ为散射和透射系数.值得一提，上述的讨论也可以推广到导线本身含有自旋轨道耦合的情形,此外,对中间散射区没有作任何几何形状、哈密顿量具体形式等的规定.

1.2导线为Helicalmetal的情形[8]

所谓一维Helical metal,就是指在一般的能量上只有1对互为时间反演的载流态.最著名的例子就是二维自旋量子霍尔态(QSH)的边界态[17].在无限长的QSH条带的几何结构中，2个边界距离较远， 就可以分别看成是相互独立的2根Helical导线.此外，普通的一维导线可以看成2根通向同一电极的Helical导线.这时，本质上只是用不同的次序来标记载流态而已.

一般地，导线上的散射态波函数可写为

定义a=(φinL,φinR)T和b=(φoutL,φoutR)T，可得式(3)和式(4),进一步对式(10)两边同时作用时间反演，可得

根据Θ不变性得

结合式(4)可得

以上推导依然可以直接地推广到含有任意根Helical导线的情形.因此，在所有导线是Helical导线的散射问题中(普通导线亦可看成一对Helical导线)，散射矩阵是反对称的.对奇数维的反对称矩阵，有det(S)=0.结合散射矩阵的幺正性，可知|det(S)|=1.因此，可断定含有奇数根Helical导线的散射问题是物理上不允许存在的.由此可得出一些重要的推论：二维和三维拓扑绝缘体的边界/表面态必定是连通的[8].

2 单轴应变的石墨烯纳米力学共振体系中的散射问题

众所周知，石墨烯的低能哈密顿量可由如下二维Dirac模型描述[18]：

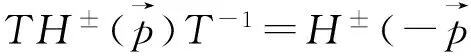
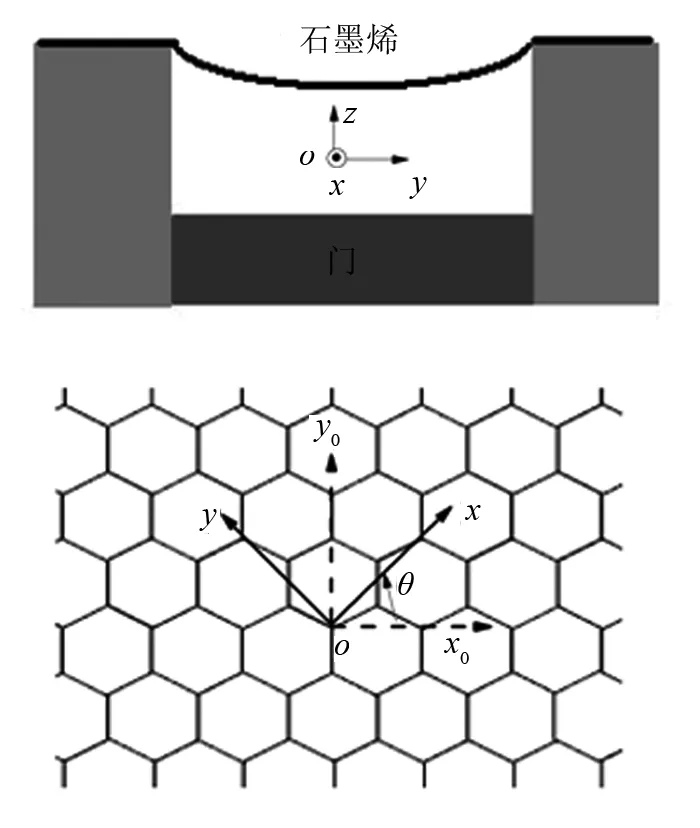
x轴相对Zigzag方向转动了θ角[18]图1 悬挂在沟槽上的石墨烯的纳米力学共振体系

考虑悬挂在沟槽上的石墨烯的纳米力学共振体系(见图1)[20].由于在高度方向的形变，低能下的有效模型[21]为

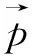
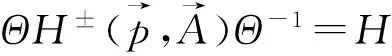
可以证明此时膺规范势[20]为

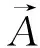
可以证明此时体系具有中心反演对称性

在x方向是无限的(x平移不变)几何结构中，可以对每个给定的kx求解一维散射问题.在两端对称的情况下，由式(18)可以证明

将振幅t,r代入绝热泵浦电流的计算公式[22-23]，很容易得到如下对称形式：

此即文献[20]中的式(3).此处我们从中心反演对称性得到这个结果，比文献[20]中解析求解反射和透射系数的方法更加简洁和直接.式(18)反映了中心反演对称性对散射矩阵的约束.然而，在式b=Sa中，若对入射波和出射波各自作规范变换U和V(至少可以对不同的态做不同的U(1)规范),则S→VSU-1, 即可在表面上改变散射矩阵的对称性.在文献[20]中，有关散射系数的对称性的式(16)并没有直接体现中心反演对称要求(注意若有rd(kx,θ)=r-d(kx,-θ)，结合文献[20]中的式(10)，则可直接体现中心反演对称性)，其原因正在于规范的选取(即波函数基的选取)没有直接反映中心反演对称性.

3 含Majorana费米子体系的输运性质

最近几年，凝聚态物理学领域的一个最热门话题之一是在凝聚态体系中制备和检测Majorana费米子.在相对论量子力学中，Majorana费米子是满足Dirac方程的实数解[24].从算符角度，它是一个电荷中性的厄米性粒子(其算符满足γ+=γ,γ2=1).根据费米子代数，任一个费米子的产生/湮灭算符可以定义1对Majorana算符，分别对应费米子算符的实部和虚部：f=(γ1+iγ2)/2.反过来，也可用

来定义1对Majorana算符.进而有iγ1γ2=2f+f-1.因此,由2个Majorana粒子总可以构造一个普通的费米子.研究表明，在满足粒子数不守恒的非常规超导(或超流)体系，有可能在体系的边界、界面或涡旋中心等处存在零能的Majorana束缚态.这种非常规超导体可称为拓扑超导体[ 25-26].最近也有许多不同的方案，通过常规超导体与拓扑绝缘体的邻近效应[27-30]及超导体与处在外磁场中有自旋轨道耦合的半导体体系的邻近效应[31]等复合结构来实现Majorana费米子.

当一维Helical金属(x<0)与拓扑超导体(x>0)接触时，界面处可存在Majorana束缚态[10，30,32].下面笔者研究此时体系典型的输运性质.体系的哈密顿量为H=H0+δH，其中δH描述接触点(x=0)的耦合项.而H0描述Helical导线的有效哈密顿量,即

引入新的单向运动的无自旋费米子算符

式(22)亦可写成

在小于超导体体能隙的能量范围，超导体只通过接触点的Majorana算子(若超导体处在拓扑相时)与Helical导体耦合，能量为E的准粒子激发算符一般可写成

式(24)中：PE和HE分别是准粒子的粒子和空穴成分；γ为界面处的Majorana束缚态.为描述体系的遂穿性质，可定义如下散射矩阵形式：

由于BDG方程的粒子空穴对称性，再加上Helical metal的费米子自由度为1的特点(因此没有冗余的简并自由度)，有Γ+(E)=Γ(-E),进而可以得到S(E)=τxS*(-E)τx.进一步考虑S矩阵的幺正性，可推得零能处S的2种标准形式：

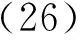
(27)

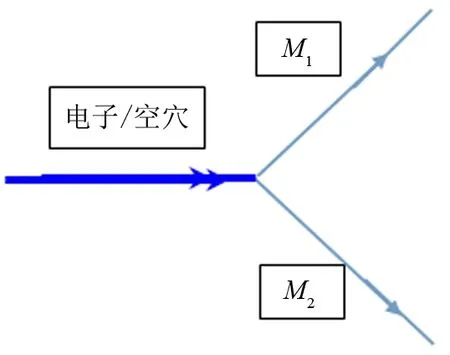
图2 单向运动的电子/空穴模式与2个Majorana模式的散射示意图

此外，基于二维拓扑超导体边缘的手征Majorana模式的输运性质也被广泛研究[27-29].其中一个典型的问题是,一个单向导通的手征导电模式(用BDG的语言，即一对单向导通的的粒子/空穴模式)与2个手征Majoranna模式接触于一点而形成的散射问题(见图2).在三维拓扑绝缘体的表面，通过超导和铁磁体材料的接触作用可形成的各种准一维通道，即可构成图2中的各种单向运动模式[27-29].在超导和铁磁体之间就可产生手征Majorana模式，其运动方向可由铁磁体的磁化方向来控制.2块反向的铁磁体之间形成的波导通道，可存在手征导电模式(如量子霍尔效应的边缘态).如图2所示，假设准粒子由两铁磁体间的波导通道入射，并由2个Majorana模式出射，此问题的散射态准粒子算符可写成

式(28)中:γ1(E),γ2(E),e(E),h(E)分别是手征Majorana模式以及电子和空穴模式对应的算符，可以用如下方式定义散射矩阵：

式(29)中，a,b,c,d分别是准粒子中2个Majorana模式的成分以及电子、空穴成分.考虑到粒子空穴对称性引起的Γ-E=Γ+E(一般体系无其他的简并的一维模式)，以及γ1,2(E)+=γ1,2(-E)和e(E)+=h(-E),h(E)+=e(-E)，可推得

再加上SS+=1，可推得零能下散射矩阵的一般形式[29]:

这个形式在准粒子单向通道通过2条Majoiran路线到达另一侧的单向通道输运性质的研究中起到了核心的作用[10-11,28-29].

2012年，人们在实验上通过输运性质的测量看到了Majorana粒子存在的若干实验证据[33-35].

4 结 论

在本文中，笔者结合了近些年自己的一些研究工作，以及最近的一些前沿问题，对几个介观体系中的散射矩阵形式作了有关对称性分析的介绍.在我们讨论的问题中，除了准粒子数守恒要求导致散射矩阵的幺正性，体系的对称性(如时间反演、中心反演、粒子空穴对称性等),对散射矩阵也给出一些重要的限制.在某些情况下，我们就能通过这些条件确定散射矩阵的解析形式,这对理解体系的输运性质是非常重要的.在有些情况下，我们甚至因此可以得到体系电子结构的拓扑性约束(如拓扑绝缘体的表面态/边界态的连通性证明[8]).在文献上，散射矩阵的研究还被推广到对系统的拓扑性质的理论分类上.总之，散射矩阵的对称性质分析的确是关于介观体系的一个重要研究工具.

[1]阎守胜,甘子钊.介观物理[M].北京：北京大学出版社，2000.

[2]Datta S.Electronic transport in mesoscopic systems[M].Cambridge:Cambridge University Press,1997.

[3]Buttiker M.Four-terminal-phase-coherent conductance[J].Phys Rev Lett,1986，57(14)：1761-1764.

[4]Nikolic′ B K,Souma S,Zrbo L P,et al.Nonequilibrium spin hall accumulation in ballistic semiconductor nanostructures[J].Phys Rev Lett,2005,95(4):046601.

[5]Jiang Yongjin,Hu Liangbin.Symmetry properties of spin currents and spin polarizations in multiterminal mesoscopic spin-orbit-coupled systems[J].Phys Rev B,2007,75(19):195343.

[6]张俊杰,张艳娜,邱宇,等.从散射波函数方法中导出的非平衡格林函数公式[J].浙江师范大学学报:自然科学版,2009,32(1):59-64.

[7]Katsnelson M I,Novoselov K S,Geim A K.Chiral tunnelling and the Klein paradox in graphene[J].Nature Physics,2006，2:620-625.

[8]Jiang Yongjin,Lu Feng,Zhaifeng,et al.Connectivity of edge and surface states in topological insulators[J].Phys Rev B,2011,84(20): 205324.

[9]Sen D,Deb O.Junction between surfaces of two topological insulators[J].Phys Rev B,2012,85(24)：245402.

[10]Alicea J.New directions in the pursuit of Majorana fermions in solid state systems[J].Rep Prog Phys,2012，75(7)：076501 .

[11] Beenakker C W J.Search for Majorana fermions in superconductors[J].Annu Rev Con Mat Phys,2013，4:113-117.

[12]Meidan D,Micklitz T,Brouwer P W.Topological classification of adiabatic processes[J].Phys Rev B,2011,84(19):195410.

[13] Fulg I C,Hassler F,Akhmerov A R.Scattering theory of topological insulators and superconductors[J].Phys Rev B,2012,85(16):165409.

[14]Roland Winkler.Spin-orbit coupling effects in two-dimensional electron and hole systems[M].Berlin:Springer-Verlag,2003.

[15]常凯，杨文.半导体中自旋轨道耦合及自旋霍尔效应[J].物理学进展，2008,28(9)：236-262.

[16]Jiang Yongjin,Lu Xiaoli,Zhai Feng.Standard form of the scattering matrix for time reversal symmetric system[J/OL].[2013-10-15].http://www.arxiv.org/abs/1310.1733.

[17]Wu Congjun,Bernevig B A,Zhang Shoucheng.Helical liquid and the edge of quantum spin hall systems[J].Phys Rev Lett,2006,96(10):106401.

[18] Castro Neto A H，Guinea F,Peres N M R，et al.The electronic properties of graphene[J].Rev Mod Phys,2009,81(1):109-162.

[19] Beenakker C W J.Colloquium:Andreev reflection and Klein tunneling in graphene[J].Rev Mod Phys,2008,80(4):1337-1354.

[20]Jiang Yongjin,Low T,Chang Kai,et al.Generation of pure bulk valley current in graphene[J].Phys Rev Lett,2013，110(4):046601.

[21]Vozmediano M A H,Katsnelson M I,Guinea F.Gauge fields in graphene[J].Phys Rep,2010,496(4/5):109-148.

[22]Brouwer P W.Scattering approach to parametric pumping[J].Phys Rev B,1998,58(16):R10135-R10138.

[23]Moskalets M,Buttiker M.Floquet scattering theory of quantum pumps[J].Phys Rev B,2002，66(20)：205320.

[24]Pal P B.Dirac,Majorana and Weyl fermions[J].Am J Phys,2011,79(5):485-498.

[25]Kitaev A Y.Fault-tolerant quantum computation by anyons[J].Ann Phys(N.Y.),2003，303(1):2-30.

[26]Nayak C,Simon S H,Stern A,et al.Non-Abelian anyons and topological quantum computation[J].Rev Mod Phys,2008,80(3):1083-1159.

[27]Fu Liang,Kane C L.Superconducting proximity effect and Majorana Fermions at the surface of a topological insulato[J].Phys Rev Lett,2008,100(9):096407.

[28]Fu Liang,Kane C L.Probing neutral Majorana Fermion edge modes with charge transport[J].Phys Rev Lett,2009,102(21):216403 .

[29]Akhmerov A R,Nilsson J,Beenakker C W J.Electrically detected interferometry of Majorana Fermions in a topological insulator[J].Phys Rev Lett,2009,102(21):216404.

[30]Law K T,Lee P A,Ng T K.Majorana Fermion induced resonant andreev reflection[J].Phys Rev Lett,2009,103(23):237001.

[31]Lutchyn R M,Sau J D,Sarma S D.Majorana Fermions and a topological phase transition in semiconductor-superconductor Heterostructures[J].Phys Rev Lett,2010,105(7):077001.

[32] Fidkowski L,Alicea J,Lindner N H,et al.Universal transport signatures of Majorana fermions in superconductor-Luttinger liquid junctions[J].Phys Rev B,2012,85(24):245121.

[33]Mourik V,Zuo K,Frolov S M,et al.Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices[J].Science,2012,336(6084):1003-1007.

[34]Deng M T,Yu C L,Huang G Y,et al.Observation of Majorana Fermions in a Nb-InSb nanowire-Nb hybrid quantum device[J/OL].[2013-10-15].http://www.arxiv.org/abs/1204.4130.

[35]Rokhinson P L,Liu Xinyu,Furdyna J K.Observation of the fractional ac Josephson effect:the signature of Majorana particles[J].Nature Physics，2012,8(11):795-799.

(责任编辑 杜利民)

Discussiononthesymmetrypropertiesofscatteringmatrixofsomemesoscopicsystems

JIANG Yongjin, XU Yong

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

Taking scattering matrix as an important theoretical tool for characterizing the transport property of mesoscopic systems with quantum coherence, it was discussed the quantum scattering problem for several mesoscopic systems, which included: 1)spin-orbital coupled systems with time reversal symmetry; 2)graphene with uniaxial strain which preserves inversion symmetry; 3)two typical problems related to Majorana Fermion(Chiral Majorana Fermion and Majorana bound states). The symmetry property of scattering matrix from the symmetry of the system was deduced, and some qualitative understanding of the transport property were obtained. It was also pointed out that in some cases, even topological properties of electronic structure of the system could be predicted.

scattering matrix; symmetry; spin-orbital coupling; graphene; Majorana Fermion

O488

A

1001-5051(2013)04-0379-07

2013-06-08

国家自然科学基金资助项目(11004174)

蒋永进(1975-)，浙江东阳人，教授，博士.研究方向：凝聚态物理和理论物理.