基于石墨烯块材料的谷过滤器*
2013-10-25翟峰,汪娟
翟 峰, 汪 娟
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
基于石墨烯块材料的谷过滤器*
翟 峰, 汪 娟
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
综述了石墨烯谷电子学的部分研究进展;探讨了在二端石墨烯块材料中产生谷极化电流的可能性.在块材料中,有2种与谷自由度直接耦合的势能:应变产生的赝矢量势和依赖于子晶格的静电势(交错势能).对称性分析表明,仅靠这2种势能的作用不能产生谷极化的输出电流.若将这2种势能分别和普通的磁电垒联合,就能获得显著的谷过滤效应.利用交错势能和磁电垒联合调制产生的谷电流可通过逆谷Hall效应测量.
石墨烯;谷电子学;谷过滤器;应变;交错势能
0 引 言
石墨烯中的电子具有多个内禀自由度,除了通常的自旋和电荷自由度外,还包括谷自由度(源于2个不等价的Dirac点)和赝自旋自由度(源于2套不等价的子晶格).借鉴半导体电子学中对电子自旋自由度的研究思路[1],石墨烯能带的二重谷简并特性已被用于设计电子器件,谷电子学应运而生.石墨烯的2个谷(K和K′ 谷)由时间反演操作联系在一起.石墨烯块材料中“谷”间散射源于短程无序势(附加原子、点缺陷等),其平均自由程可达到1 μm.谷电子学的基本问题之一是如何产生谷极化的电子分布.基于具有zigzag边界的石墨烯条带和静电调制,Beenakker研究小组[2]设计了一种只允许某个谷的电子通过的器件.2个平行排列的“谷”过滤器则构成1个“谷”阀门.“谷”阀门的电流抑制源于zigzag型石墨烯条带中电子隧穿的宇称效应.K和K′谷在zigzag型条带中是独立的,在armchair型条带中混合在一起.2种纳米条带的杂合提供了一种调制谷极化的可能途径[3].这些设计方案需要精确控制石墨烯条带的边界,很难得到广泛应用.在远离Dirac点处,由于石墨烯能谱的三角弯曲效应,电子的群速度依赖于谷自由度.这个特性可用于产生高度谷极化的电子束[4].
以上这些研究都侧重于谷极化的电场控制.本文将基于石墨烯块材料,探讨谷极化的磁场调控.这种研究思路可移植到硅烯、MoS2等新兴材料中.
1 模型和公式
磁场在自旋电子学[1]和谷电子学中扮演的角色不同.在自旋电子学中,磁场是控制自旋的常用手段.外磁场可通过塞曼效应极化电子自旋,在具有大因子的半导体中,这种自旋-磁场耦合作用表现更为明显.对于方向随空间变化的非均匀磁场,电子的不同自旋分量还会发生混合.相比之下,石墨烯中的谷间散射和能级的谷劈裂即使在磁场达到104T时也可以忽略.自旋电子学中的自旋轨道耦合提供了一种通过改变载流子的轨道运动来调节其自旋态的途径.当二端波导体系的输出端处于单通道输运区时,由于时间反演对称,单独靠自旋轨道耦合不能在波导体系中产生自旋极化[5].在谷电子学中,有2种机制类似于自旋电子学中的自旋轨道耦合,它们是平面应变和子晶格依赖的静电势UAB.
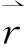
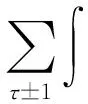
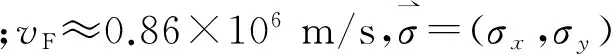
由哈密顿 (1) 配合适当的边界条件可构成一个散射问题.它的求解通常比较复杂.本文只考虑体系沿某个方向平移不变的简单情形.若将这个方向取为y轴,则动量分量py=ћky守恒.对位于τ谷、能量为E、横向波矢为ky的电子,其波函数可写为[11]
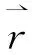
式(2)中:旋量ψτ(x,ky)满足Hτ(ky)ψτ(x,ky)=Eψτ(x,ky);τ谷电子的哈密顿量Hτ为

对此散射问题,电子的透射几率T=Tτ(E,ky)可通过散射矩阵的数值方法[12]来计算.对于给定的费米能EF,在低温TK(绝对温度的单位为E0/kB)下,谷相关的电导表达式为
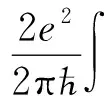
式(4)中:f(E)={1+exp[(E-EF)/TK]}-1是费米-狄拉克分布函数;Tτ(E,ky)=|tτ(E,ky)|2为透射几率;Ly是样品沿y方向的尺寸.以下数值计算中将电导单位取为G0=e2Ly/(2π2ћ).体系的总电导和谷极化的表达式为

2 对称性分析
当磁垒不存在时,哈密顿量(3)满足对称性[13]

这意味着Tτ(E,ky)=T-τ(E,-ky),即K′谷电子的透射谱可由K谷电子的透射谱经过相对ky=0 的镜像对称操作得到.结合式(4)~式(5),给出谷极化P=0.因此,对我们考虑的体系,磁垒是产生谷极化的必要条件,仅靠弹性形变和交错势不能够在二端石墨烯器件中产生谷极化.值得指出的是,若不施加局域磁场和应变场,则τ谷电子的透射谱自身相对ky=0具有镜像对称[14],即

当磁垒和衬底应变同时作用到石墨烯薄膜上时,K谷和K′谷在倒空间将发生大小不相等的位移.这足以产生谷过滤.不施加应变,仅靠磁垒和均匀的交错势UAB能否产生谷极化?为了回答这个问题,笔者写出ψτ=(ψτ+,ψτ-)T的2个分量在ASy≡0时满足的微分方程[13]

当∂xUAB=∂xU=0时,F±τ=0,方程(10)与谷指标无关.因此,这种情形不能产生谷极化.若想利用磁垒和均匀的交错势产生谷极化,还需静电调制(∂xU≠0).
3 数值结果和讨论
以2个简单的体系为例,说明利用应变场与局域磁场的组合、交错势能与局域磁场的组合来产生谷过滤的可行性.
图1 给出了第1个体系的结构示意图,应变发生在宽度为LS的区域.宽度为LS的铁磁条沉积在介电层(图中的灰色层)上,产生局域磁场.这是一个应变石墨烯谷过滤器,局域磁场由磁化强度沿x轴的铁磁条产生.为简单起见,相应的磁矢势以及应变产生的规范势近似取为

式(11)中:AM和LM分别表示磁势垒的强度和宽度;xM=LS+D;D是磁势垒和应力区间的距离;Θ(x)是Heaviside台阶函数.标量势U在应力区和磁垒区的高度均为US,在其他区域为零.为了减少可调参数的数目,统一选取结构参数为LM=LS=D=1,设定磁垒高度AM=2.

图1 应变石墨烯谷过滤器
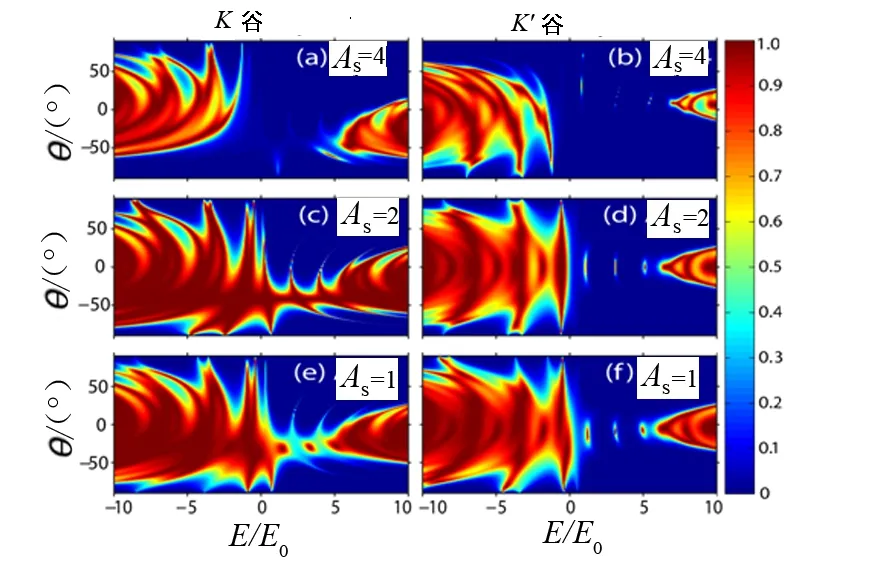
图2 电子透射几率随入射能量和入射角的变化
图2给出了谷相关的透射几率Tτ随入射角θ=arcsin(ky/E)和入射能量E的变化.图2中,US= 3,应变强度AS从上到下分别取值4,2,1.从图2中观察到透射几率的角各向异性和共振隧穿.这可从磁垒和应力区域存在的衰减模来理解[15].由于这种情况对矢势分布有很强的依赖性,所以K和K′谷的电子透射谱会有很大的差异.实际上,在图2中也看到,入射能量E在某些范围内,K谷的电子能够在很宽的θ区域内透射穿过系统,而K′谷的电子却在所有的θ区域内全部反射回去.电子传输也可以由应变强度AS来调制.AM远大于AS的情况下,传输的各向异性主要由磁势引起.当AS远大于AM时,传输的各向异性则主要由应变引起.这种特征可由E<0的传输谱看出.在给定的参数条件下,对正能量入射,AS=AM时,K谷和K′谷的电子传输差别最显著.

图3 谷相关的电导和谷极化随费米 能量EF 的变化(温度TK = 0.5)
图3是针对图1中的体系计算谷相关的电导和谷极化随费米能量EF的变化.K谷和K′谷的电子传输差异在电导上也可以反映出来.图3给出了谷相关的电导和相应的谷极化曲线.共振传输的存在使零温电导存在强烈的振荡.这种振荡在相对高的温度TK= 0.5时就被消除了.由图2可知,EF<0 时,电导主要决定于max(AS,AM),而且对谷的依赖比较小.因此,主要集中讨论EF>0的情况.EF>US时,K谷电子的电导普遍大于K′谷电子的电导.这个现象可以从磁垒区和应力区狄拉克点的位置移动(δkM和δkS)来理解.在K谷,狄拉克点的位移δkM和δkS是同方向的,而在K′谷,位移δkM和δkS是反方向的.δkM和δkS平行移动的情况比反平行移动的情况具有更多的传播通道.当传播通道被矢势耗尽时,电导Gτ受到抑制.注意到在很宽的能量区域中,电导G+1显著不为零而电导G-1接近零.基于这个特征,笔者提出的器件能过滤出K′ 谷的电流而产生谷极化电流.在总电导比较显著的某些区域可得到超过80%的谷极化.类似于自旋流,谷电流在线性响应区可由ΔG=G+1-G-1表征.在费米能较高的区域ΔG随EF变化很小,而此时极化P单调减小.
上述模型计算表明,利用应变场与局域磁场的组合可在石墨烯块材料中产生具有显著谷极化的电流.改变应变AS的符号或反转铁磁条的磁化方向都会改变谷极化的极性.如何探测输出电流的谷极化?目前提出的探测机制有2种:1)石墨烯在正常区/超导区的Andreev反射[16];2)石墨烯空间反演破缺时的逆谷Hall效应[9].若利用这2种机制来探测图 1 中体系产生的谷极化,都需另行设计精巧的实验装置.这也是目前多数谷过滤方案面临的问题.对谷电子学而言,最好能在同一个体系中实现谷极化的产生和探测.为此,笔者考虑均匀的交错势能与局域磁场的组合,在石墨烯的绝缘层上沉积铁磁金属条或超导金属条可获得所需的局域磁场.图4是基于交错势和局域磁场调制的石墨烯谷过滤器,阴影区域为介电层.输出电流的谷极化可用逆谷Hall效应测量.静电调制由在金属栅极上施加电压产生,在样品的两侧接上电压探针.当右侧的输出端电流存在谷极化时,电压探针将发生偏转[9].
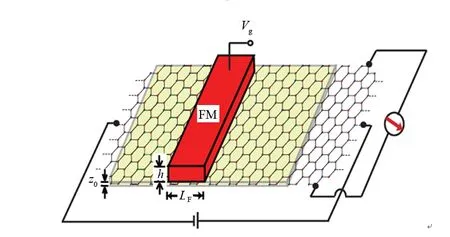
图4 交错势和局域磁场调制的石墨烯谷过滤器
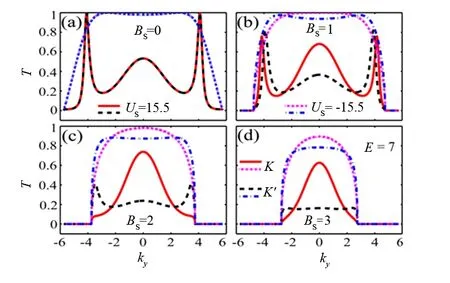
图5 电子透射几率随横向波矢ky的变化
对图4的体系,在磁场和电势都是矩形分布的情形下,即

笔者可给出透射几率的解析表达式.式(12)中的BS,US都是常数,BS>0,UAB>0.在磁垒区0 对给定的入射能E>UAB或E<-UAB,波矢ki,k0实际上不依赖于谷指标τ.引入符号 其中Dp(X)是p阶抛物圆柱函数.τ谷电子的透射几率可写为 式(18)中:k-i=ki-ikyi;k+0=k0+iky0.这个表达式对谷指标τ的依赖来自参数γτ.当US=0时,显然有T+=T-.这和前面的对称分析是一致的. 对矩形的磁电垒,图5 画出了透射几率(式18)随横向波矢ky的变化曲线.图5中交错势能取为UAB=4,入射能量取为E=7,结构参数为L=2,US=±15.5,BS=0,1,2,3.透射曲线相对ky=0是镜像对称的.这是因为,当矢势Ay(x)关于某条中心线x=xc呈反对称分布(同时电势呈对称分布)时,操作σzRx将Hτ(ky)变为Hτ(-ky).此处Rx是反射操作x→2xc-x.当BS=0时,透射几率不依赖于谷指标 ,见图5(a).从图5(a)还可看出,当US>2UAB,即电子发生带间隧穿时,透射曲线上可能出现显著的Fabry-P′erot共振峰.对小的BS,透射几率的谷简并被解除,原来的共振峰将发生劈裂.随着磁垒高度BS的增大,见图5(b)~图5(d),一些共振峰向|ky|大的方向移动并最终消失,T+,T-的差别可能增大.相对带内隧穿(US<0)而言,带间隧穿(US>2Δ)可导致更显著的谷差异.这可从γ±对磁垒和电垒高度的依赖关系来理解.由于零温电导G±正比于T±对ky的积分,图5(b)~图5(d)展示的透射几率曲线意味着非零的谷极化. 本文基于二端石墨烯块材料,讨论了谷极化电流产生的可能性.笔者考虑了2种谷相关的势能:应变产生的赝矢量势和依赖于子晶格的静电势(交错势能).对称性分析给出了利用这2种势能产生谷极化的必要条件.通过2个具体模型的计算,发现这2种势能和局域磁场、静电势能的联合可能产生显著的谷过滤效应.利用交错势能与磁电垒联合调制产生的谷极化可通过逆谷Hall效应测量. [1]ŽuticI,Fabian J,Das Sarma S.Spintronics:Fundamentals and applications[J].Rev Mod Phys,2004,76(2):323-410. [2]Rycerz A,Tworzydlo J,Beenakker C W J.Valley filter and valley valve in graphene[J].Nat Phys,2007,3(3):172-175. [3]Zhang Zhenzhong,Chang Kai,Chan K S.Resonant tunneling through double-bended graphene nanoribbons[J].Appl Phys Lett,2008,93(6):062106. [4]Garcia-Pomar J L,Cortijo A,Nieto-Vesperinas M.Fully Valley-Polarized electron beams in graphene[J].Phys Rev Lett,2008,100(23):236801. [5]Zhai Feng,Xu Hongqi.Symmetry of spin transport in two-terminal waveguides with a spin-orbital Interaction and magnetic field modulations[J].Phys Rev Lett,2005,72(8):085314. [6]Neto A H C,Guinea F,Peres N M R,et al.The electronic properties of graphene[J].Rev Mod Phys,2009,81(1):109-162. [7]Zhou Shuyun,Gweon G H,Fedorov A V,et al.Substrate-induced bandgap opening in epitaxial graphene[J].Nature Mater,2007,6:770-775. [8]Vitali L,Riedl C,Ohmann R,et al.Spatial modulation of the Dirac gap in epitaxial graphene[J].Surf Sci,2008,602(22):L127-L130. [9]Xiao Di,Wang Yao,Niu Qian.Valley-Contrasting physics in graphene:magnetic moment and topological transport[J].Phys Rev Lett,2007,99(23):236809. [10]Guinea F,Katsnelson M I,Geim A K.Energy gaps and a zero-field quantum Hall effect in graphene by strain engineering[J].Nature Phys,2010,6:30-33. [11]Zhai Feng,Zhao Xiaofeng,Chang Kai,et al.Magnetic barrier on strained graphene:a possible valley filter[J].Phys Rev B,2010,82(11):115442. [12]Xu Hongqi.Scattering-matrix method for ballistic electron transport:theory and an application to quantum antidot arrays[J].Phys Rev B,1994,50(12):8469-8478. [13]Zhai Feng,Chang Kai.Valley filtering in graphene with a Dirac gap[J].Phys Rev B,2012,85(15):155415. [14]Zhai Feng.Valley filtering in gapped graphene modulated by an antisymmetric magnetic field and an electric barrier[J].Nanoscale 2012,4:6527-6531. [15]Zhai Feng,Chang Kai.Theory of huge tunneling magnetoresistance in graphene[J].Phys Rev B,2008,77(11):113409. [16]Akhmerov A R,Beenakker C W J.Detection of Valley Polarization in graphene by a superconducting contact[J].Phys Rev Lett,2007,98(15):157003. (责任编辑 杜利民) Valleyfiltersbasedonbulkgraphene ZHAI Feng, WANG Juan (CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China) It was reviewed some progresses in graphene valleytronics. The feasibility of generating a valley-polarized current in two-terminal bulk graphene systems was discussed. It was showed that there existed two kinds of potentials coupling directly with the valley degree of freedom: strain-induced pseudo vector potential and sublattice-dependent electrostatic potential (staggered potential). It was found from the symmetry analysis that the two potentials alone could not produce a valley polarization in the output current. It was also found that remarkable valley filtering could be achieved when electrons in bulk graphene were modulated by the combination of a conventional magnetic-electric barrier with either of the two potentials. The valley current obtained from the combination of a staggered potential and a magnetic-electric barrier could be detected by means of the inverse valley Hall effect. graphene; valleytronics; valley filter; strain; staggered potential O488;O484 A 1001-5051(2013)04-0386-06 2013-05-30 国家自然科学基金资助项目(11174252) 翟 峰(1976-),男,湖北应城人,副教授,博士.研究方向:理论凝聚态物理.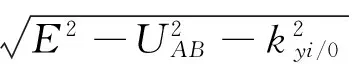
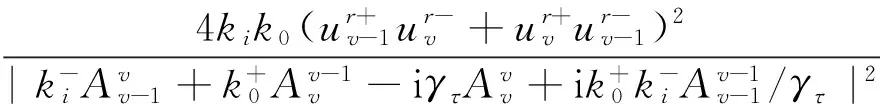
4 结 论
