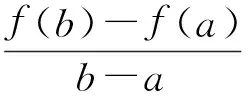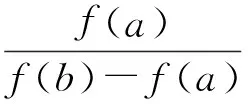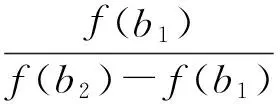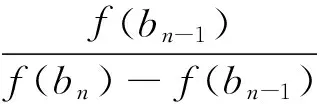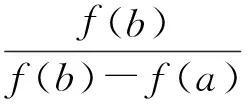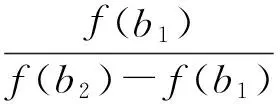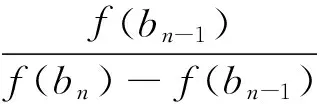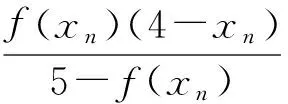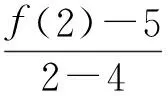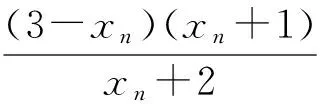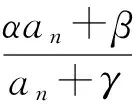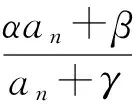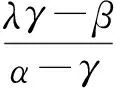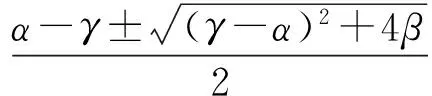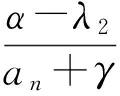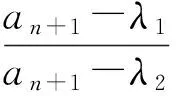高等数学背景下的高考命题探究——2012年全国数学高考理科卷第22题

●

(嘉定区第一中学 上海 201808)

高等数学背景下的高考命题探究
——2012年全国数学高考理科卷第22题

●杨思源

(嘉定区第一中学 上海 201808)

题目设函数f(x)=x2-2x-3，定义数列{xn}如下：x1=2,xn+1是过点P(4,5),Qn(xn,f(xn))的直线PQn与x轴交点的横坐标.

(1)证明：2≤xn

(2)求数列{xn}的通项公式.

评析本题考查运用数学归纳法论证递推数列{xn}的单调性，并求递推数列的通项公式；考查考生的推理论证能力和利用递推关系式与待定系数法探求数学通项公式的能力.本题背景深刻，立意高远，它是高等数学背景下的一道居高临下、深入浅出的高考试题.它的背景源于高等数学中用插值法求方程近似解，其原理如下：

假定实系数多项式f(x)=0在区间[a,b]有唯一的根ξ，且f′(x)=0和f″(x)=0在[a,b]内无根，即各自保持符号不变.联结曲线y=f(x)的2个点A(a,f(a))与B(b,f(b)),设弦AB与x轴交点为b1(其坐标也可记为b1，下同)，b1作为根ξ的一次近似值.为了求出更接近的近似值，需分2种情况进行讨论.

(1)f(b1)与f(b)异号，如图1所示.

联结弦B1B，交x轴于b2，b2为ξ的二次近似值，依次进行下去，可得ξ的一系列近似值.这时，取a作为0次近似值.

图1 图2

(2)f(b1)与f(a)异号，如图2所示.

联结弦AB1，交x轴于b2，b2为ξ的二次近似值，同情况(1)，依次可得ξ的一系列近似值.不过，这时应取b作为ξ的0次近似值.

那么，从f(x)及f″(x)的符号上如何区分这2种情况呢？

容易看出，在情况(1)中，a在曲线y=f(x)凹面的一侧，此时f(a)与f″(x)异号；而情况(2)是b在曲线凹面的一侧，此时f(b)与f″(x)异号.无论哪种情况，都是取f(x)的函数值与f″(x)异号的那个端点作为0次近似值.下面找出递推规律.

(1)当f(a)与f″(x)异号时，直线AB的两点式方程为

令y=0，可得弦AB与x轴交点b1的坐标

同理

…

一般地，有

(2)当f(b)与f″(x)异号时，类似地可求得

…

一般地，有

在上述2种情况下，序列a(或b)，b1,b2,…,都是从曲线的凹面单调地收敛于根ξ.

图3

在这个原理的背景下，命题者选择了简单的函数f(x)=x2-2x-3，其零点为-1和3.如图3,函数f(x)=x2-2x-3在区间[2,4]上连续，f′(x)=2x-2>0，f″(x)=2>0,且f(2)=-3<0,f(4)=5>0.

此题满足原理中的第1种情况，即

f(2)=-3<0,f″(x)>0.

若取x1=2，则第n+1次根的近似值满足递推关系

即

由原理知，满足此种情况的数列{xn}：2≤xn

这样第(1)小题便解决了.

当然，此题也可用初等数学的方法作如下解答：

过点Q1(2,f(2))和点P(4，5)作一直线PQ1:

由2≤x1

由2≤x1

依次类推可得

式(3)与式(4)相除，得

故数列{xn}的通项公式为

利用函数的不动点求分式线性递推数列的通项公式，也是借助于高等数学中的线性微分方程的特征根法而得到的一种方法，其原理说明如下：

解引入待定参数λ，使

当a1=λ时，an=λ(n∈N*)；

当a1≠λ时，an≠λ(n∈N*),此时可求出

(由αγ≠β可知λ≠α).

当(γ-α)2+4β≠0时，有

从而

由此可求出an.

仍成立，因此

不难看出，本题的产生源于方程近似解的线性插值法和利用函数的不动点求数列的通项公式.本题以高等数学的知识为背景，居高临下，深入浅出进行高考命题，让考生运用初等数学的思维方法来解决，不仅有利于揭示初等数学与高等数学知识的联系，更有利于考生进入高校进一步的学习与深造，也有利于教师的专业知识的可持续发展.

[1] 李师正.多项式代数[M].济南：山东教育出版社，1983：265-267.