城市已有应急物资储备库功能优化模型与实证研究——以石家庄市为例

陆相林，高树芳，刘春玲，赵 宁

（石家庄学院 经济管理系，河北 石家庄 050035）

20世纪70年代以来，国际社会极其关注以提高城市安全度为目标的重大灾害应急管理体系的建设。几乎所有重大突发事件的处置都伴随着大量的应急物资供应活动，有效的应急系统可将事故损失降低到无应急系统的60%。[1]3自1998年建立国家级应急物资储备制度起，中国现已在10个省会城市设立了国家级应急物资储备库，但总体上仍无法适应新时期备灾、救灾的要求。《国家综合减灾“十二五”规划》明确指出，必须新建、改建和扩建一批符合标准的应急物资储备库。

应急物资储备库从行政隶属上看可分为救灾物资储备库和物资储备库两大类，前者隶属于民政部门，后者直属国家物资储备管理局。河北储备物资管理局受中华人民共和国国家发展和改革委员会国家物资储备局垂直领导，同时受河北省委省政府领导。主要职责之一就是协调地方政府和国家应急储备物资管理工作，做好国家或本地区发生突发事件的物资保障工作。现有12个直属处，在石家庄市域内有3个，分别为：一三三处、一三五处、一五零处。本文所研究的应急物资储备库功能优化主要指这三个物资储备库的功能优化问题。

为了降低救灾（备灾）物资调度的运行费用，提高工作效率，要充分考虑应急物资储备库的合理布局，正确地选择其地理位置。对应急物资储备库空间组织问题进行研究，为突发事件处置提供必要的物质基础是战略决策问题，本质上决定着整个应急公共服务体系的成效。

一、相关研究综述

设施选址问题（facility location problem，简称FLP）是关于人类活动空间组织、资源优化的学问，是管理科学、产业经济学、数学关注的重要研究领域之一，对医疗、消防、工商业等各方面而言，都极为重要。[2-4]国外设施选址研究文献较经典的有：Francis等对1983年以前的有关选址问题的模型进行了验证、总结，并提出了相应的算法。[5]Brandeau等对等级选址问题进行了分类综述。[6]Drezner和Hamacker对2002年前的设施选址理论进行了系统的归纳。[7]1-25Farahani和Hekmatfar则对2002-2009年之间的设施选址理论进行了系统梳理与总结。[8]1-80国内方面，陆相林、侯云先对国内外最新设施选址理论进行了概述，在此基础上提出了考虑覆盖半径内需求满意差异的选址问题。[9-11]当前，设施选址研究主要集中于模型构建、算法设计与空间决策支持三个方向，主要应用于物流规划、应急设施选址等方面，与应急物资储备库空间组织与优化相结合的成果较少。

应急物资储备库方面的研究成果主要以定性描述建设现状、提出相关对策与建议为主，定量研究成果相对较少，有关已有应急物资储备库功能优化的研究成果更少。定性研究中，冉岚回顾了中国物资储备的历史状况，提出必须建设信息共享的储备系统，完善储备的布局，更新物资储备的管理理念。[12]张永领提出了中国应急物资储备体系完善的基本思路。[13]定量研究中，郭子雪、齐美然、张强研究了基于梯形模糊数的应急物资储备库最小加权距离选址模型，并给出求解该问题α-水平最优解的算法。[14]葛春景、王霞、关贤军基于轴辐理论，提出应对重大灾害的轴辐式应急物资储备网络体系构建思路。[15]陆相林、侯云先、林文等对国家级应急物资储备库、小城镇应急物资储备库选址问题进行了探讨与实证研究。[9，11]

本研究旨在实现城市区域内已有应急物资储备库整体物资调度服务的最优化，建立体现已有应急物资储备库功能优化本质的数学模型，完成算法设计，并以石家庄市为实证区域，解决其已有应急物资储备库功能优化问题。

二、城市已有应急物资储备库功能优化模型

城市已有应急物资储备库功能优化涉及两类站点：一类为应急物资需求站点，另一类为应急物资储备库。应急物资储备库为应急物资需求站点的人们提供应急物资。已有应急物资储备库功能优化是指在城市中已经存在应急物资储备库的情景下，通过建立优化模型，确定各应急物资储备库服务的具体需求点以及服务半径，实现各应急物资储备库对各应急物资需求点服务的最优化的过程。

实现城市区域内已有应急物资储备库整体物资调度服务的最优化，响应速度是其中必须考虑的重要因素，因此，可采用距离或者时间来表示应急物资储备库、应急物资需求点之间的空间联系紧密程度，为了简化分析且不失一般性，本文仅以距离为例进行分析。

（一）假设

（1）应急物资需求点、应急物资储备库以点状存在。（2）应急物资储备库与应急物资需求点之间以航空、公路、铁路等交通方式①联通。（3）应急物资储备库和应急物资需求点之间的距离可通过调查或者计算得到。（4）为了保证应急救助效率和反映应急管理实际，假设各需求点总是得到离其最近的应急物资储备库的服务。（5）只考虑一个需求点最多只能被一个应急物资储备库提供服务的情况。（6）由于应急物资储备库建设与维护成本较高，故个数要有限制，设为p。

（二）符号定义

为了讨论分析的方便，进行如下的符号定义。

i代表应急物资需求点；I表示应急物资需求点的全体；j代表应急物资储备库；J表示应急物资储备库的全体；p为实际可选择建立的应急物资储备库数；ai表示应急物资需求点i的人口数量；k指代某种交通方式，K为应急物资采取的交通方式全集，有k∈K②；dijk为应急物资被采取k种交通方式运输时，应急物资储备库i至应急物资需求点j的矩离；hi是表达需求点i应急物资需求紧急程度的参数，取值为[0，1]③本文实证时不考虑hi的差异，即假定hi==1。；为应急物资由应急物资储备库j至应急物资需求点i时，采取k种交通方式时所实现的应急需求点人们满意程度差异的参数，本文主要考虑距离因素和交通方式的影响，因此有xijk为0-1变量，应急物资采取k种交通方式运输时，如果应急物资需求点i被应急物资储备库j提供服务，则取1值，否则，取0值；yjk指 0-1变量，应急物资采取k种交通方式运输时，如果应急物资储备库j被选择进行设施建设，则取1值，否则，取0值。

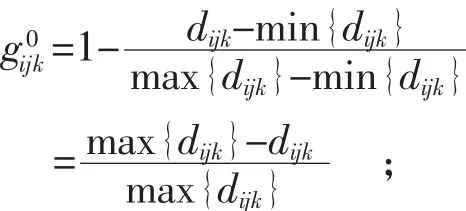
（三）模型

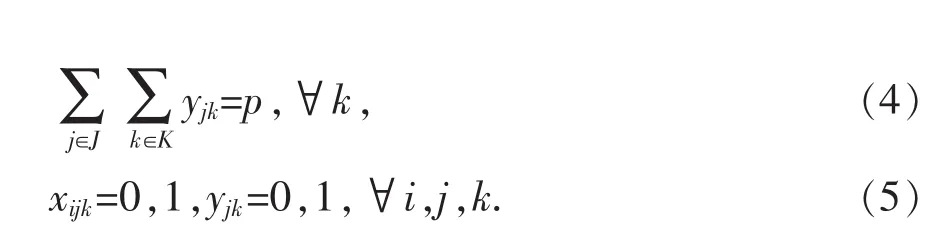
其中，目标函数（1）使被服务的应急物资需求点的总满意程度最大，gi0jk表示采用k类交通方式时第i个应急物资需求点接受第j个应急物资储备库服务时的满意程度，取值范围为[0，1]，本文主要考虑距离因素和交通方式对gi0jk的影响；约束（2）保证只有应急物资储备库j在k种交通方式下服务于应急物资需求点 i时，才有 xijk=1，否则，xijk=0；约束（3）强化应急物资储备库的服务效率，保证每一个应急物资需求点最多只可由一个应急物资储备库提供服务，消除各应急物资储备库间的重复服务问题；（4）指定将要建设的应急物资储备库个数为p；约束（5）限制决策变量xijk和yjk为0-1整数变量。

由于本文考虑已有应急物资储备库的功能优化，因此有 yjk==1，坌j，k。 因此式（2）变为

式（5）变为

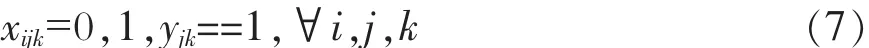
因此，得到本文的已有应急物资储备库功能优化模型：

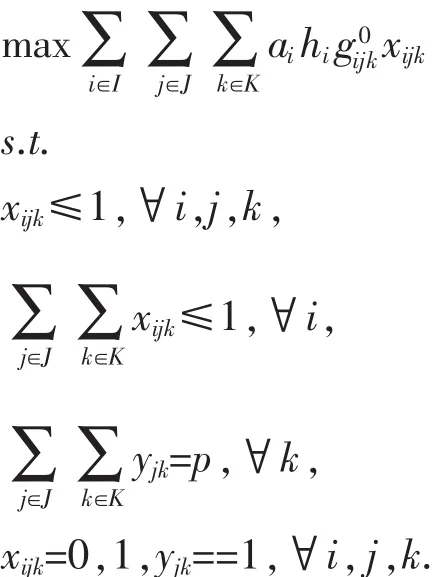
三、石家庄市已有应急物资储备库功能优化

（一）研究区概况

石家庄市地理位置为东经 113°30′-115°20′，北纬 37°27′-38°47′。 现辖 6 个区、12 个县、5 个县级市，总面积1.58万平方千米，常住人口939.5万，其中市区面积455.8平方千米，人口231.3万。2011年，石家庄市提出在2-3年时间内完成市、县两级救灾物资储备库建设和改造任务，形成以市救灾物资储备库为中心，以县级储备库为配套，以社区（乡、镇、街道）爱心超市或捐赠站（点）为补充的全市救灾物资储备机制。

（三）优化依据与算法设计

基于功能优化模型，对石家庄市现有应急物资储备库进行优化配置。石家庄市各区县代表应急物资需求点，应急物资储备库与需求点之间距离用公路交通距离表示，数据根据我要地图网①网址为http://www.51ditu.com。的测距功能测得，因篇幅所限，具体数据此处省略。

本文所建模型属于最大覆盖问题，是NP-hard问题[16，17]。对于大型的此类问题的求解，精确算法以及一般的商业优化软件无能为力，只能借助于启发式或近似算法，以及人工智能等算法（如蚁群算法）来求得近似解。

如前符号定义中所述，本文只考虑公路一种交通方式，有k==1，且不考虑石家庄市各区县应急物资需求的紧急程度差异，因此可令hi==1。

由于本文属功能优化问题，应急物资储备库已经确定，即对于任意应急物资储备库j，都有yjk==1。模型求解的任务是确定xijk的值。基于上述特点，笔者提出以下启发式算法求解思路。

第一步：初始化各参数。对 ai，hi，k赋值，根据所测得的需求点至应急物资储备库距离矩阵，利用式

第二步：对任一需求点i，计算其被各应急物资储备库服务时的各值，比较各应急物资储备库对应的值，取其最大者对应应急物资储备库，设为j，并验证约束条件式。如满足，则令xijk=1。如不满足，则取为第二大的应急物资储备库，设为 j′，再次验证约束条件，如满足，则令，其他=0，如不满足，则依次类推。

第三步：重复第二步，直至所有的需求点都完成第二步。

（三）优化结果

根据相关调查数据，利用matlab7.0编写算法程序，在PC机windows xp环境下运行通过，求得如下结果（见表1）。

表1中第1列列出的是石家庄市现有的3个应急物资储备库，分别为：石家庄鹿泉市一三三处、石家庄市区一三五处、石家庄井陉县一五零处。

由表1第2列可以看出，鹿泉市一三三处服务范围内的区县为行唐县、灵寿县、平山县、鹿泉市，石家庄市区一三五处服务范围内的区县 （市）为长安区、桥东区、桥西区、新华区、裕华区、正定县、栾城县、高邑县、深泽县、赞皇县、无极县、元氏县、赵县、辛集市、藁城市、晋州市、新乐市，井陉县一五零处服务范围内的区县（市）为井陉县、井陉矿区。

表1第3列显示了石家庄市3个现有应急物资储备库的服务半径与最远服务区县（市）：鹿泉市一三三处的服务半径为52.1千米，最远服务区县（市）为行唐县；石家庄市区一三五处的服务半径为74.8千米，最远服务区县（市）为深泽县；井陉县一五零处服务半径为11.1千米，最远服务区县（市）为井陉矿区。

（四）石家庄市应急物资储备库功能优化布局图

基于表1，结合原始数据和上述分析，得到石家庄市现有应急物资储备库功能优化布局图，见图1。由图1可知：（1）通过本文提出的功能优化模型，对各应急物资储备库功能加以优化，实现了以各应急物资储备库——区、县（市）有机结合的组团结构，但区域结构明显不均衡，突出表现为石家庄市区一三五处的服务负担过重，承担了石家庄市23个区、县（市）单位中的17个，占总数的73%。（2）3个应急物资储备库在石家庄市的空间分布过于集中，都集中于距石家庄市中心40千米（公路距离）以内的区域，鹿泉市一三三处至石家庄市中心的距离为16.0千米，石家庄市区一三五处至市中心的距离为5.7千米，井陉县一五零处至石家庄市中心的距离为39千米。

表1 石家庄市现有3个应急物资储备库功能优化结果

图 1 石家庄市现有应急物资储备库功能优化布局图

（五）石家庄市应急物资储备库功能优化建议

在石家庄市现有的3个应急物资储备库中，建议重点加强一三五处的建设，石家庄市应采取多项措施与之沟通、协作，实现重大突发事件下的有效联动。由表1和图1可知，一三五处需要服务的区、县（市）数目较多，达17个，发生重大突发事件时可能物资供应任务繁重。石家庄市应从救助车辆数量、类别，交通联系，专业人员配置和建设资金等方面给予支持与合作。

建议石家庄市适当扩建、设立远离市区镇的应急物资储备库，以进一步优化应急物资供应功能。如前所述，石家庄市3个应急物资储备库在石家庄市的空间分布过于集中，都集中于距石家庄市中心40千米（公路距离）以内的区域，以致于各偏远区、县，即远离现有应急物资储备库的区、县应急物资需求有可能得不到及时供应。如石家庄市区一三五处至深泽县的服务半径为74.8千米，至辛集市的服务半径为69.2千米。此外，考虑到平山县县域面积较大

[1]吴宗之，刘茂.重大事故应急救援系统及预案导论[M].北京：冶金工业出版社，2003.

[2]REVELLECS，EISELTH A.Location Analysis：A Synthesis and Survey[J].European Journal of Operational Research，2005，（1）：1-19．

[3]REVELLECS.A Bibliography for Some Fundamental Problem Categories in Discrete Location Science[J].European Journal ofOperationalResearch，2008，（3）：817-848.

[4]GOLDBERG J.Operation Research Models for the Deployment of Emergency Services Vehicles[J].EMSManagement Journal，2004，（1）：20-39.

[5]FRANCISR L，MCGINNISLF，WHITEA.Location Analysis[J].European JournalofOperationalResearch，1983，（12）： 220-252.

[6]BRANDEAUM L.An Overview of Representative Problems in Location Research[J].Management Science，1989，（6）：645-674.

[7]DREZNERZ，HAMACHERHW.Facility Location：Applications and Theory[M].Berlin：Springer，2002.

[8]FARAHANIR Z，HEKMATFARM.Facility Location：Concepts，Models，Algorithms and Case Studies[M].Berlin：Physica-Verlag，2009.（由图1可知），其县政府距下辖村镇仍有一段距离，且路况较差。因此，建议石家庄市除了已有的3个应急物资储备库外，需至少新增深泽县、辛集市、平山县3个应急物资储备库。

应加强石家庄市应急物资储备库的相关配套设施建设与有关活动的开展。首先应加强与石家庄市应急物资储备库联系的交通设施建设，保证至少有市级公路相通。其次，应以石家庄市为中心，建立市级、区县级应急物资储备服务体系，并开展交流、协作，做到重大突发事件中的高效合作、互助。

四、结语

本文以创造应急物资需求点民众总体最大满意程度为目标，构建了考虑交通方式、需求点风险程度的城市已有应急物资储备库功能优化模型，解决了城市应急公共服务体系中应急物资储备库与应急物资需求点最优空间联系问题。把所建模型应用于石家庄市3处已有应急物资储备库的功能优化，得出了较为合理的结果。

进一步的研究可以考虑公平准则 （又称公共服务均等化）下的应急物资储备库布局优化问题，城市避难场所、防火设施的功能优化问题。

[9]陆相林，侯云先.基于设施选址理论的中国国家级应急物资储备库优化配置[J].经济地理，2010，（7）：1 091-1 095.

[10]陆相林，侯云先，林文，等.基于设施选址理论的小城镇应急医疗服务中心功能优化[J].经济地理，2011，（7）：1 119-1 123.

[11]陆相林，侯云先.基于选址理论的小城镇应急物资储备库优化配置——以北京房山区为例[J].地理研究，2011，（6）：1000-1008.

[12]冉岚.从汶川地震看国家物资储备建设[J].宏观经济管理，2008，（9）：60-62.

[13]张永领.我国应急物资储备体系完善研究[J].管理学刊，2010，（6）：54-57.

[14]葛春景，王霞，关贤军.应对重大灾害的轴辐式应急物资储备网络体系[J].自然灾害学报，2011，（2）：153-160.

[15]郭子雪，齐美然，张强.应急物资储备库最小加权距离选址模型[J].计算机工程与应用，2009，（34）：195-198.

[16]HAKIMISL.Optimum Locations of Switching Centers and the Absolute Centersand MediansofaGraph[J].Operations Research，1964，（3）：450-459.

[17]HAKIMISL.Optimum Distribution of Switching Centerson a Communications Network and Some Related Graph Theoretic Problems[J].Operations Research，1965，（3）：462-475.